基于车辆对道路不满意度的微观换道决策
屈文涛, 李文锐, 王勇, 徐剑波, 贺旭飞
(1.西安石油大学机械工程学院, 西安 710065; 2.中国石油长庆油田分公司质量安全环保部, 西安 710018)
随着物流行业的发展,汽标委智能网联汽车分标委在关于《自动驾驶物流车标准需求研究报告》中提出干线自动驾驶物流车[1]主以载货汽车为主,且行驶场景主要为高速公路,行驶平均车速为60~100 km/h。载货汽车在高速公路环境中换道是车辆的基本驾驶行为之一[2],目前车辆换道的研究大部分停留在换道辅助系统上,对于自动驾驶汽车而言自主换道时机的判断是一个较为复杂的过程。另外多数自动驾驶换道决策研究以轿车为主,目前对商用载货车辆讨论的较少。
从1986年第1个车道变换模型GIPPS模型提出开始,国内外对换道行为决策已经有大量的研究,常用的有STIRAS、MITSIM模型[3-4]等。大多数研究将换道过程分为换道意图的产生、目标车道的选择(包括换道可行性分析)和换道过程的执行。文献[5-7]基于贝叶斯人工智能网络结合NGSIM数据集对网络连接权重进行训练学习,最终得到可以判断换道可能性的贝叶斯网络模型,网络用来判别给定条件下换道行为是否能够发生以及发生的概率大小。文献[8]构建分层Logit模型定量分析驾驶人换道行为决策过程,但机器学习的方法需要大量训练数据,泛用性得不到保证且可解释性差。聂琳真等[9]建立模糊决策来判断换道意图。决策将本车与本车前车和邻近车道前后车的车头时距作为模糊输入,再结合模糊规则和驾驶员性格因子得到不同性格下的换道意图,但缺乏对换道和跟车安全性的定量分析。不能保证换道意图产生过程中本车与前车之间的距离是否满足换道与跟车的安全性要求。陈慧等[10]结合预测模型对车辆运动进行预测,并提出一种车道不满意度累积算法来计算预测时域内的本车不满意度累积。当不满意度累积值超过阈值且本车满足换道安全性时可触发换道。但该道路不满意度计算方法假设本车已经理想跟驰行驶,而实际换道意图产生时本车可能并未处于稳定跟车工况,没有考虑本车未达到稳定跟车前的换道意图。
基于以上问题,现提出一种适用于高速场景自动驾驶商用载货车的换道决策模型。先根据道路交通法规对载货商用车车速和制动减速度的限制要求求出车辆的理想跟车安全距离。再依据本车的跟车安全距离提出一种模糊决策系统来推算本车对行驶车道的不满意度。本文研究中设计两种道路不满意度计算方法分别应对本车未达到目标车速行驶和已经达到目标车速行驶工况下对道路不满意度的计算。当本车不满意度达到阈值就会触发换道意图,当换道意图产生后只要满足换道安全就会触发换道行为。最后本文的换道决策与仿真实验在MATLAB/Simulink软件下进行搭建和验证。
1 道路不满意度算法
1.1 换道场景
高速公路的车道形式大部分为同向三车道及以上,当车辆位于最左侧或最右侧的边缘车道时,车辆只能在本车道、其右侧或左侧车道运行行驶。当车辆位于中间车道时车辆也只能在本车道或中间车道的左侧和右侧运行。无论车辆是换道或跟车行驶高速公路都可以简化为同向双车道的形式。因此本文将高速公路的驾驶场景简化为同向双车道的结构来进行研究。
1.2 本车理想安全跟车距离
为了定量分析本车在前车跟驰状态下的安全性,这里引入安全距离的概念[11]。安全距离特指车辆在前车跟驰状态下时,为保证不发生碰撞前提下与同车道前车的最小车间距离。此安全距离能够在任何突发状况下避免与前车发生相撞事故。高速公路驾驶场景的跟车行为发生在直线行驶阶段。依据汽车制动理论可得车辆的制动距离s如式(1)所示。
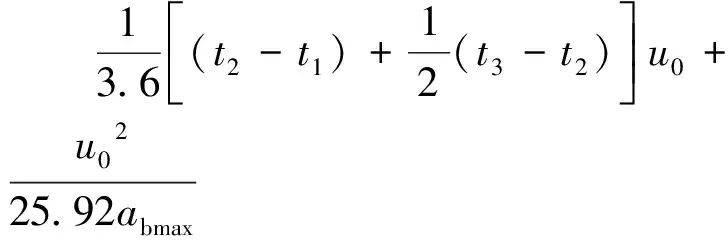
(1)
式(1)中:u0为初始车速;最大制动减速度为abmax;t1~t2为鼓式制动器的刹车蹄与制动鼓接触并压紧所需要的时间,由于较短故在制动理论分析中可忽略此时间;t2~t3为制动轮缸中的液压力增长时间,货车牵引挂车时的制动器起作用时间经过特殊设计可缩短到0.4 s[12]。
鉴于本文研究对象为自动驾驶物流车,其车型为载货车车型。故选取t2~t3的时间为0.4 s,式(1)可简化为式(2)所示。
(2)
图1为自主车与其前车制动过程的车间距变化图,图1中ego为所研究的自主车辆,egof为位于自主车前方的车辆。设置自主车辆的初始速度为Vego、最大减速度为abmax,制动距离为Dbf。egof为自主车前车,初始速度为Vf,制动距离为Dbf,最大减速度为abmax。D为自主车和自主车前车的初始车间距,Vego和V′ego为自主车始末速度,Vf和V′f为自主车前车始末速度。
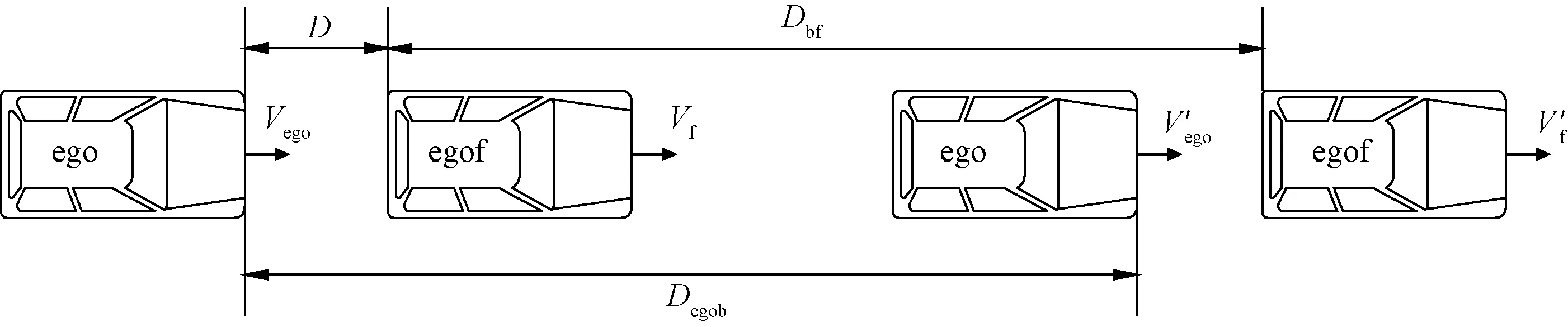
图1 自主车与前车制动过程Fig.1 Braking process of independent vehicle and front vehicle
图1中设自主车与自主车前车末速度取0。其中制动距离Degob和Dbf的计算表达式为
(3)
(4)
鉴于本文研究的自动驾驶物流车采取ABS制动且行驶场景为高速公路主干道,故路面附着系数选取为沥青或混凝土道路,附着系数选取峰值附着系数φp为0.8,故最大制动减速度amax为8 m/s2。同时制动车距还与地面附着系数μ成反比关系,因此定义辆车制动到停车后的安全储备距离SRD为式(5)计算得到[13]。
(5)
式(5)中:k取22.5;b取0.3;vego为本车初始车速。
结合式(3)~式(5)可以推得两车安全跟车车间距离Dsafe需满足式(6)。
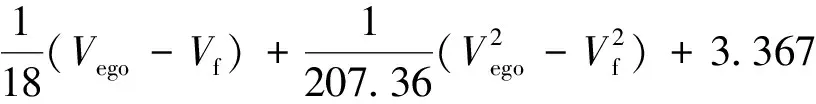
(6)
1.3 换道决策框架
高速公路的换道行为主要分强制换道和自由换道[14],强制换道主要目的是为达到特定行驶道路和区域所进行的必要换道行为[15]。而自由换道则是自主车为了追求更好的行驶环境以适应目标车速所进行的换道行为。由于自由换道在决策灵活度和复杂度上要高于强制换道,故本文研究自由换道场景下所对应的换道决策算法。首先定义道路不满意度来表示本车对当前行驶道路的不满意程度的大小。换道行为决策时,本车辆根据自身运动信息、本车周围车辆运动信息、本车行驶计划来综合判定本车对当前车道的不满意度,再判断本车对邻近车道的不满意度大小。通过将本车道和邻近车道不满意度与预设的阈值进行比较来决定换道意图的产生。其换道决策构架如图2所示。由图2知本车对当前行驶车道与邻近车道的不满意度是换道意图产生的关键。在实际高速行驶中本车的行驶工况是比较复杂的,故本文具体将可能产生换道意图的本车行驶工况分为两类。
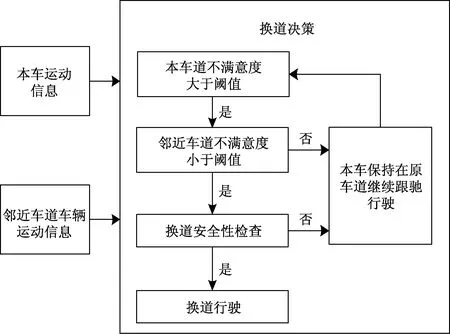
图2 换道决策构架Fig.2 Lane change decision framework
(1)工况1。本车初始状态为按照某一规划的目标速度定速巡航。此时本车为保证与前车的安全跟车距离,本车前车的运动可能会使本车的原定行驶规划无法完成,本车就会激发对本车道的不满意,本车产生换道意图。
(2)工况2。本车需要到达所规划的某一目标车速,故本车可能需要通过加速或减速来达到目标车速。为保证与前车的安全跟车距离,本车在加减速时会受到前车的运动限制而无法达到目标车速。此时本车会激发对本车道的不满意,本车产生换道意图。
1.4 道路不满意度计算
针对1.3节所提出的工况1和工况2的两种换道意图产生情景来分别计算本车对本车道与邻近车道的不满意度大小。
1.4.1 基于工况1的不满意度计算
如图3所示,对于工况1来说本车对道路的不满意度主要根据三个变量来反应,分别是本车与前车之间的距离Dc、本车与前车之间的安全跟车距离dcsafe、本车前车相对于本车的相对速度Vcf-Vc。其中Vcf为本车前车车速,Vc为本车车速。
同理为了衡量本车对邻近车道的不满意度,这里将本车向邻近车道做投影,投影得到的虚拟车拥有和本车一样的运动状态。本车对邻近道路的不满意度也主要根据三个变量来反应。分别是虚拟车与前车之间的距离Da、虚拟车与前车之间的安全跟车距离dasafe、前车相对于虚拟车的相对速度Vaf-Vac,其中Vac为虚拟车车速,Vaf为邻近车道前车车速。
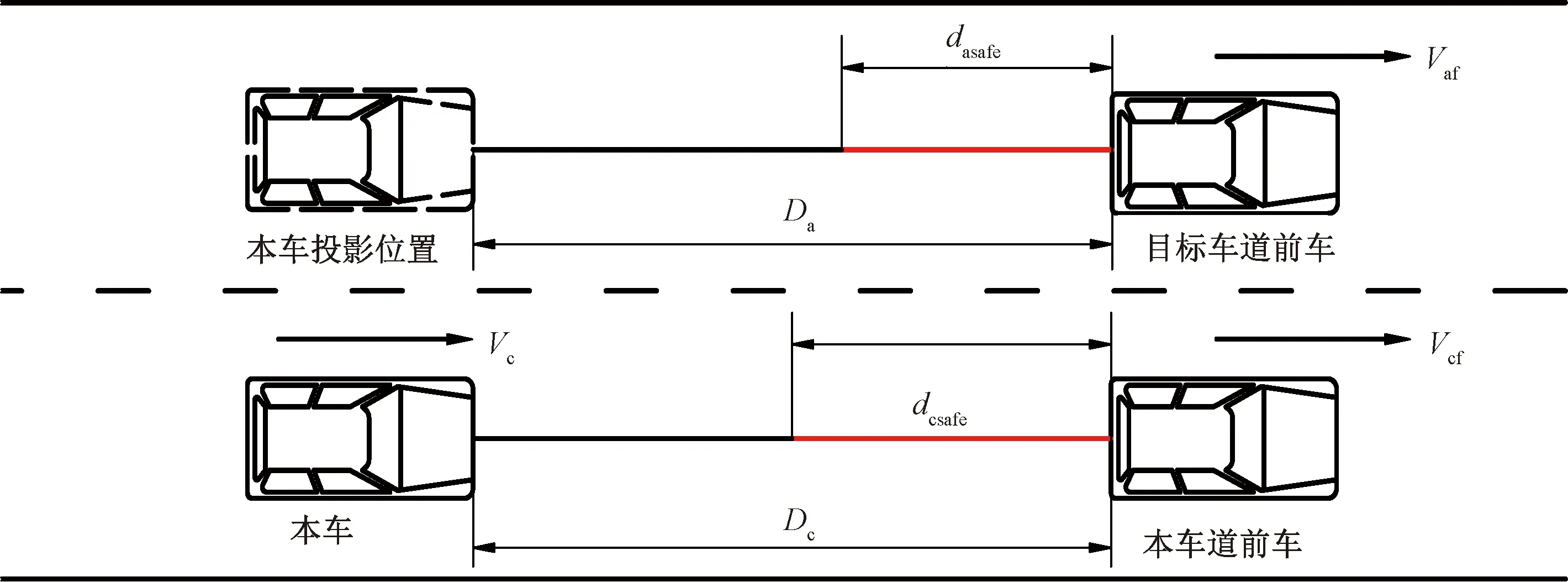
图3 工况1Fig.3 Working condition one
设计模糊推理系统来实时计算本车对本车道以及邻近车道的不满意度大小。对于一个模糊系统需要对应的模糊输入、模糊推理规则、知识库、模糊输出[16]。
为了利用模糊系统定量描述本车对道路的不满意度大小,设置Dc-dcsafe或Da-dasafe的实际论域为[0 m,30 m],语言变量分级为ZO、PS、PM、PB、PV。设置Vcf-Vc或Vaf-Vac的实际论域为[-10 m/s,10 m/s],语言变量分级为NB、NM、NS、ZO、PS、PM、PB。输入变量的隶属度函数如图4所示。输出变量为道路不满意度,实际论域范围为[0,1],隶属度函数如图5所示。当本车与本车前车的车间距越来越接近两车的安全跟车距离时本车对当前车道的不满意度就会上升,反之下降。对邻近车道的不满意度判断同理,只不过判断对象变为本车在邻近车道投影的虚拟车和邻近车道的前车。故在输入和输出变量之间定义了模糊推理规则,推理规则如表1所示。
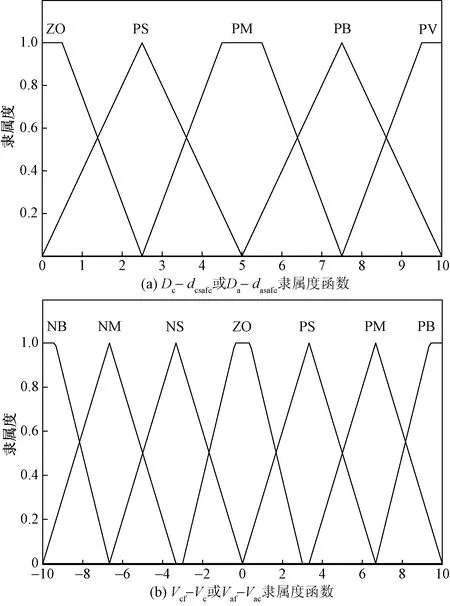
图4 输入变量的隶属度函数Fig.4 The affiliation of input variable
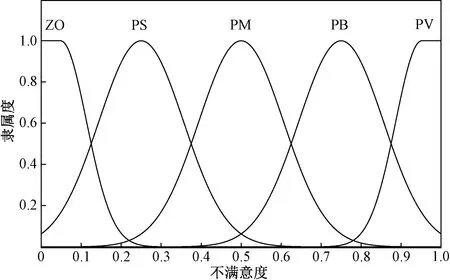
图5 不满意度隶属度函数Fig.5 Dissatisfaction affiliation function
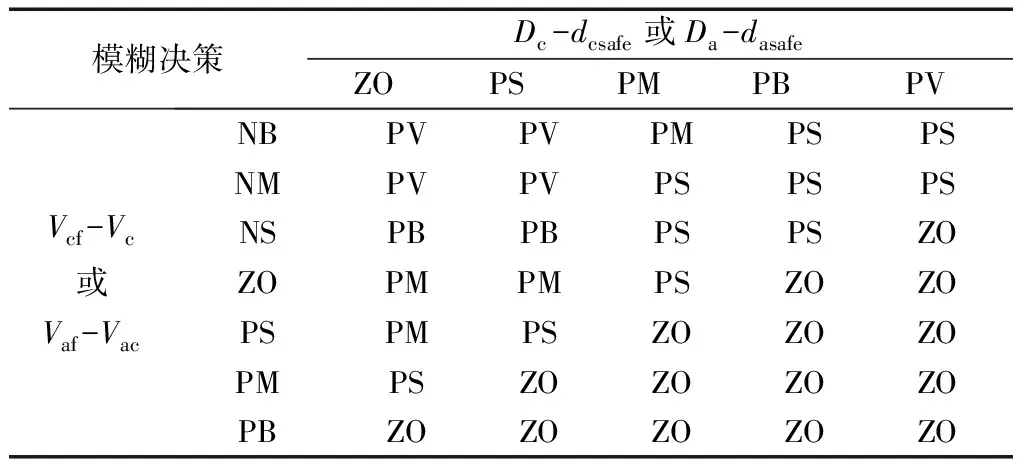
表1 工况1模糊推理规则Table 1 Fuzzy inference rule for working condition 1
1.4.2 基于工况2的不满意度计算
对于工况2来说本车需要进过一段加速或减速措施来达到本车所要求的目标车速。这里将本车加减速过程统一描述为一段加速度呈二次曲线变化的运动过程,其中本车初始和末态加速度大小均为0,故本车达到目标车速过程中的运动方程可用式(7)和式(8)来描述。
(7)
(8)
式中:t为车辆加减速过程中的任意时刻;x为t时刻下车辆沿道路中心线的纵向位移;tf为车辆从初始车速加减速到目标车速后所需的时间;v0为初始本车车速;x0为车辆加减速过程中沿道路中心线的初始纵向位移;amax为加减速过程中车辆的最大加减速度值;Vg为目标车速。
如图6所示对于工况2的讨论也需要利用本车在邻近车道的投影所产生的虚拟车来完成对邻近车道不满意度的计算。本文将本车加减速运动的初始时刻统一取值为0 s,设本车到达目标车速的终止时间为tf。对于时域(0~tf)内按采样周期TS划分时刻,每个时刻设为tk。本文假设本车前车在tk~tf时域内以tk时刻对应的车速Vcfk保持匀速运动,且移动距离为dcfk。tk时刻下本车与前车的相对距离为Dck,本车与前车之间的安全车跟车距离为dcsafe。本车加速到所需目标车速后本车的移动距离为dck,这一过程中本车相对于本车前车的移动距离为dck-dcfk。同理假设本车邻近车道前车也在tk~tf时域内以tk时刻对应的车速Vafk保持匀速运动,且移动的距离为dafk。tk时刻下虚拟车与前车的相对距离为Dak,虚拟车与前车之间的安全车跟车间距离为dasafe。虚拟车加速到目标车速后虚拟车的移动距离为dak,这一过程中虚拟车相对于前车的移动距离为dak-dafk。
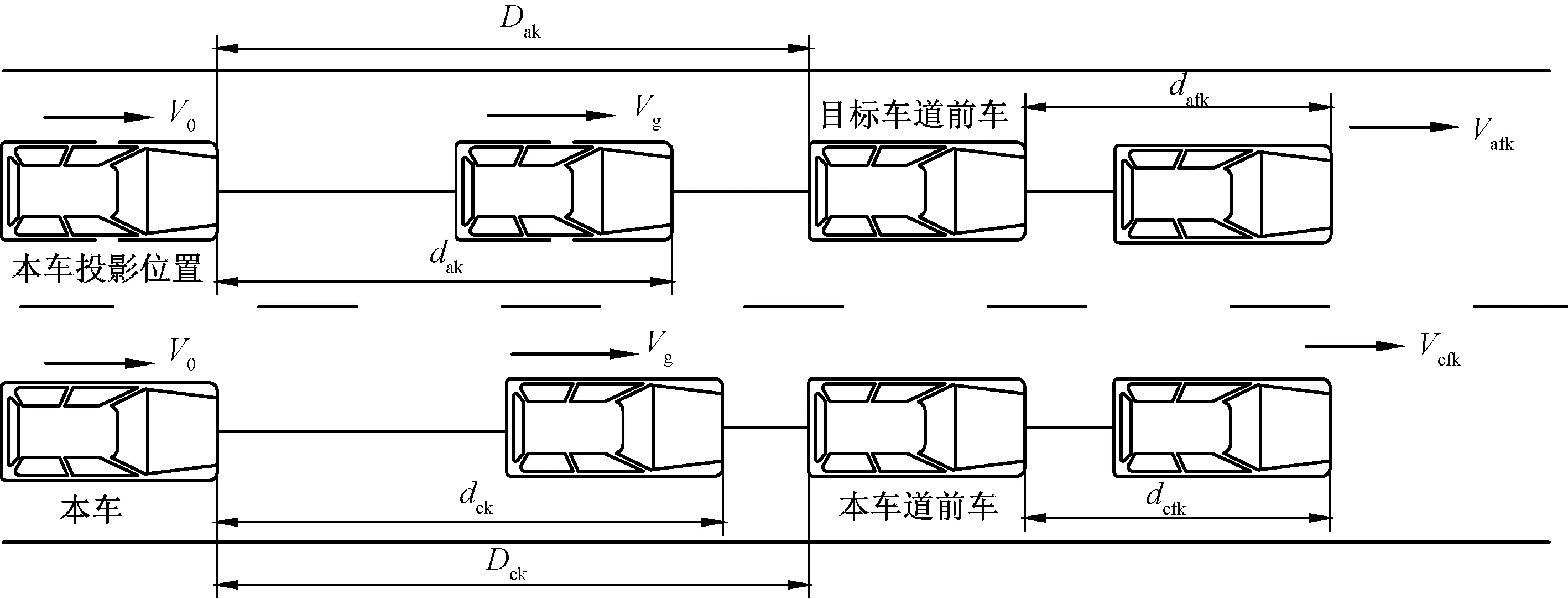
图6 工况2Fig.6 Work condition two
预测引擎会计算本车和本车在邻近车道投影的虚拟车在tk~tf内达到目标车速Vg时所行驶的距离dck和dak。由于在邻近车道的投影虚拟车与本车有相同的运动状态,故dck与dak大小相同。dck和dak的表达式为
(9)
预测引擎会计算本车加速到目标车速后相对于前车的移动距离。如果移动距离过大,在达到目标车速后就会使本车与本车前车间距过小,当间距小于或接近安全跟车距离时本车对当前车道的不满意度就会上升,反之则下降。本车对邻近车道的不满意度判断同理,只是研究的对象变为本车在邻近车道的投影虚拟车和邻近车道前车。本文利用模糊系统定量描述本车在工况2下对本车道和邻近车道的不满意度大小。设dck-dcfk或dak-dafk的实际论域为[0 m,20 m],语言变量分级为ZO、PS、PM、PB、PV。隶属度函数如图7所示。
设置Dck-dcsafe或Dak-dasafe的实际论域为[0 m,30 m],语言变量分级为ZO、PS、PM、PB、PV,隶属度函数如图8所示。输出变量为道路不满意度,输出变量的隶属度函数与图5一致。
输入和输出变量之间定义了模糊推理规则,推理规则如表2所示。

图7 dck-dcfk或dak-dafk隶属度Fig.7 dck-dcfk or dak-dafk affiliation
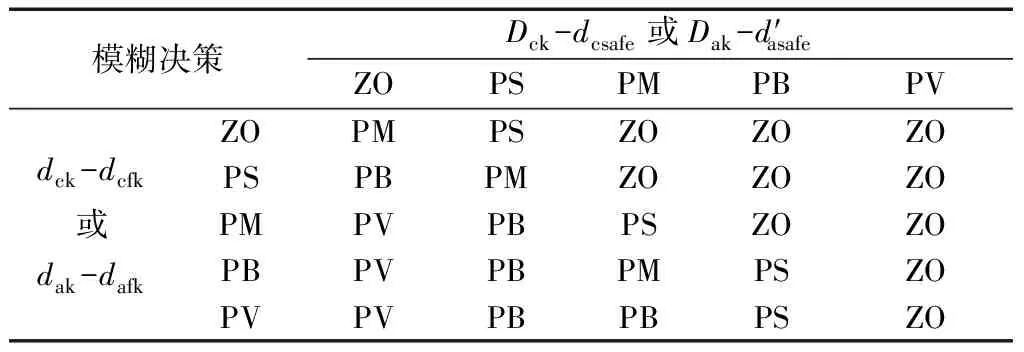
表2 工况2模糊推理规则Table 2 Fuzzy inference rule for working condition 2
2 换道安全与决策执行
2.1 换道安全分析
图9中所示的本车换道过程可以划分为3个阶段,第1阶段为换道起始时刻t0,第2阶段为中间段,此时自主车引擎盖中心压在车道线上,对应刻为t1,第3阶段为换道终止时刻t3。由于本车所在车道后车会根据本车运动自动调节加减速度以避免碰撞故本文不考虑本车后车的影响。
(1)本车道前车安全性分析。在本车换道第2阶段的t1时刻本车可能与本车道前车发生角碰,如图10所示。设换道初始时刻t0时本车与本车道前车距离为Lcf0。换道第2阶段过程中本车纵向位移为Lc,前车移动距离为Lcf。dsafe为安全余量取3.367 m。为了保持安全性必须满足
Lcf0≥Lc-Lcf+dsafe
(10)
(2)所换车道后车安全性分析。如图11所示,在本车在完成换道时本车可能与所换车道的后车发生追尾事故。设本车在整个换道过程中纵向移动距离为Lc,本车与所换车道后车的初始车间距为Lar0,整个换道过程中所换车道后车的移动距离为Lar。为了保持安全性必须满足式(11),其中dsafe为安全余量结取3.367 m。
Lar0≥Lar-Lc+dsafe
(11)

图9 本车换道示意图Fig.9 Schematic diagram of lane change
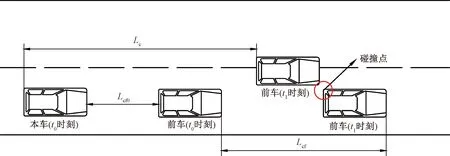
图10 本车道前车安全示意图Fig.10 Safety diagram of the vehicle ahead in this lane

图11 目标车道后车安全示意图Fig.11 Safety diagram of vehicle in front of target lane
(3)所换车道前车安全性分析。如图12所示,在本车在完成换道时本车可能与所换车道的前车发生追尾事故。设本车在整个换道过程中纵向移动距离为Lc,本车与所换车道前车的初始车间距为Laf0,整个换道过程中所换车道前车的移动距离为Laf。为了保持安全性必须满足式(13),其中dsafe为安全余量结取3.367 m。
Laf0≥Lc-Laf+dsafe
(13)
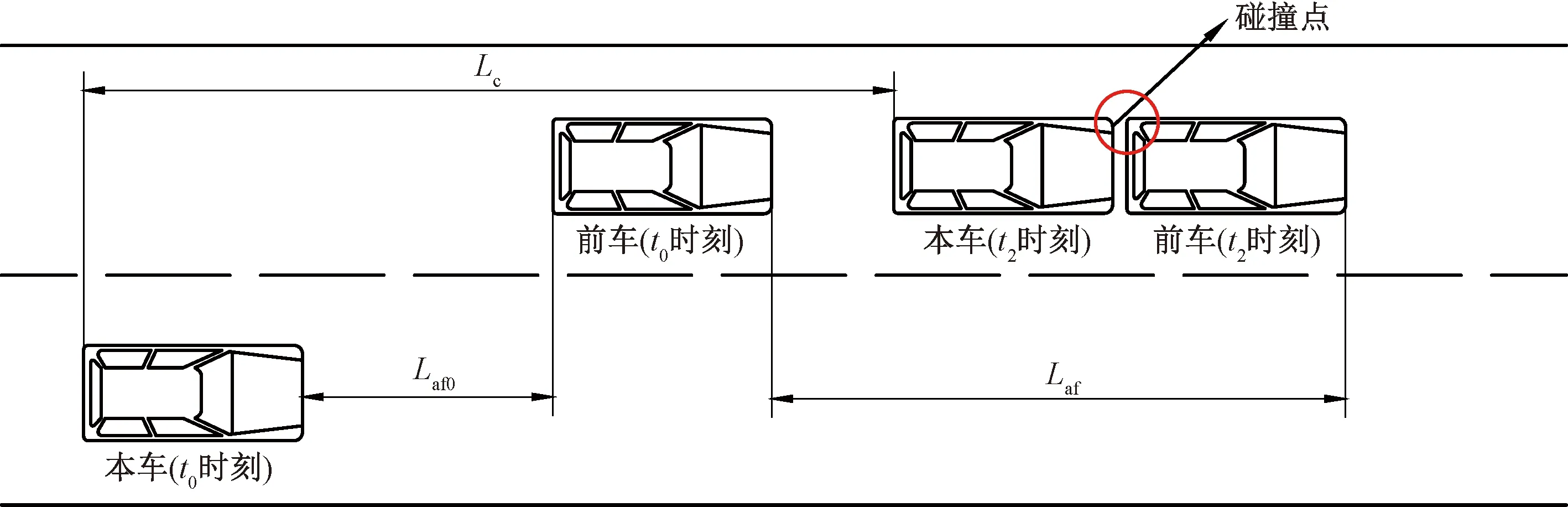
图12 目标车道前车安全示意图Fig.12 Safety diagram of rear vehicle in target lane
2.2 换道决策执行
本文所用到的换道决策模型如图13所示。当本车对本车道不满意度超过预设定的不满意度阈值且本车对邻近车道不满意度低于设定的不满意度阈值时就会触发换道意图的产生。同时为了进一步体现本文换道决策算法的优点,选取文献[9]中基于模糊逻辑的微观换道模型以进行对比,该模型利用本车与本车邻近车道前车的车间时距Taf及本车与本车所在车道前车的车头时距Tcf的差、本车与本车邻近车道后车的车间 时距Tar作为模糊逻辑输入,将换大道意愿值I作为模糊输出。当换道意愿值大于随机意愿值因子K后车辆就会产生换道意图。该模型的决策流程如图14所示。
3 仿真验证
换道决策引擎基于以下假设。
(1)对于1.4.2节描述的工况2的情形,参考文献[17],本车在正常直行时为达到目标车速所采取的最大加减速度设置为3 m/s2。换道过程中本车及其周围其他干扰车辆均保持匀速行驶,且假设车辆在车道正常直行时为沿车道中心线行驶。
(2)为了简化换道安全车距的判断,把本文设换道中间段t0-t1过程所花费的时间为换道总时间t0-t2的二分之一。由于换道持续时间较短,根据文献将换道总时间统一假设为5 s。
(3)仿真基于MATLAB/Simulink完成仿真测试任务。由于本文重点分析换道意图、换道不满意度以及跟车安全距离的变化,故仿真忽略换道过程的影响。
3.1 仿真工况配置
换道仿真场景如图15所示,设本车与本车所在道前车初始距离为Lcf0,本车所在道前车初始车速为Vcf0。本车与邻近车道前车初始间距为Laf0,邻近车道前车的初始车速为Vaf0。本车与邻近车道后车初始间距为Lcr0,邻近车道后车的初始车速为Vcr0。这里将道路不满意度阈值设置为0.5。道路几何尺寸宽为3.75 m,车道数为2。基于模糊逻辑和车头时距的微观换道模型中随机意愿值因子设为0.85。
(1)换道决策1的仿真配置:本车的初始速度为80 km/h。Vcf0为75 km/h,Lcf0为55 m。Vaf0为85 km/h,Laf0为40 m。Var0为70 km/h,Lar0为35 m。
(2)换道工况2的仿真配置:本车的初始速度为65 km/h,预计目标车速为80 km/h。Vcf0为70 km/h,Lcf0为45 m。Vaf0为85 km/h,Laf0为40 m。Var0为70 km/h,Lar0为55 m。
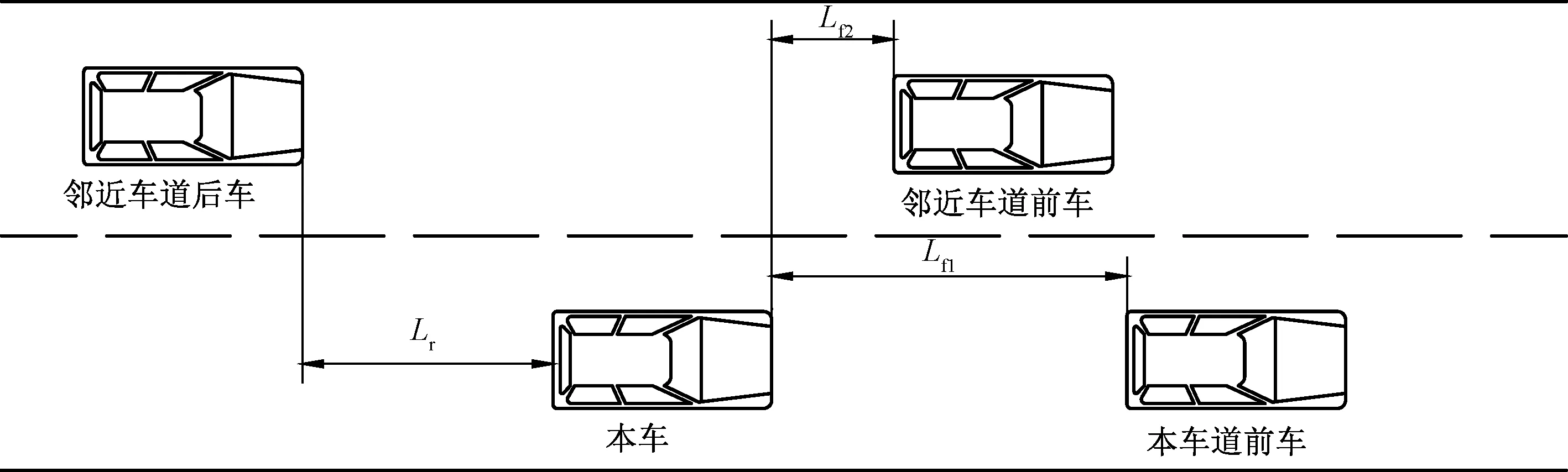
图15 仿真场景Fig.15 Simulation scenes
3.2 仿真结果
工况1的仿真环境下本车的不满意度变化和换道意愿值变化如图16所示,本车在27.08 s时对道路的不满意度大于阈值0.5,此时本车产生换道意图。在结束换道后本车对道路不满意度回落到0.078 7。同时也仿真了基于模糊逻辑和车头时距的微观换道模型,在该模型下车辆在15.04 s下换道意愿值大于随机意愿值因子0.85,此时本车产生换道意图。在结束换道后本车对道路不满意度回落到0.4以下。

图16 车道不满意度/换道意愿值变化Fig.16 Change in lane dissatisfaction/willingness to change lane values
如图17所示,为本车从原车道换道至邻近车道过程中本车与本车前车的车间距和安全跟车距离的变化。对于本文提出的道路不满意度计算模型,在27.08 s时本车才会主动换道,此时本车与本车前车距离为17.38 m,安全跟车距离为7.382 m。而对于基于模糊逻辑和车间时距的微观换道模型,本车在15.04 s产生换道意图,此时本车与本车前车距离为34.11 m,安全跟车距离为7.382 m。
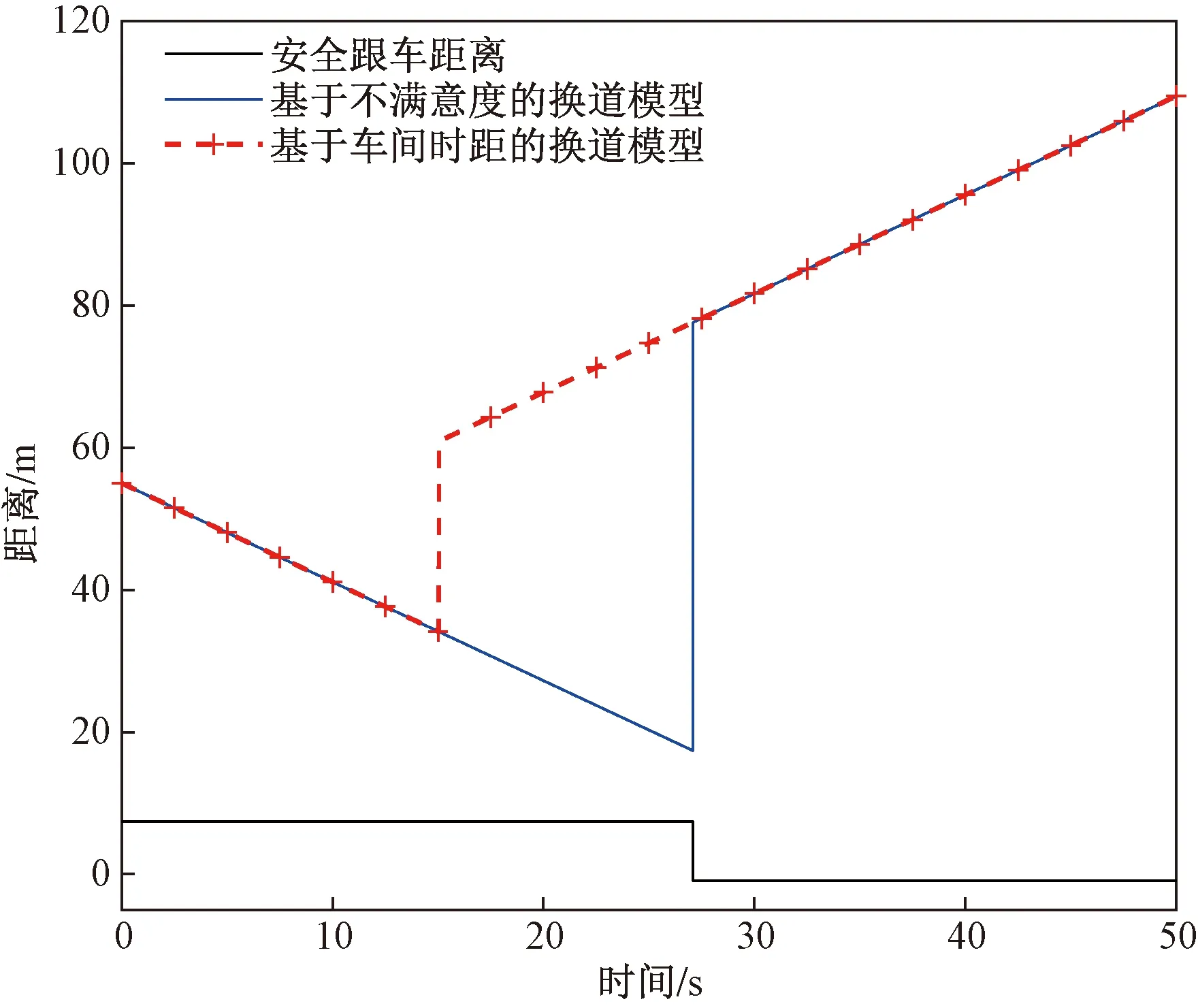
图17 本车与本车前车间距变化Fig.17 Change in distance between this car and the front of this car
工况2的仿真环境下本车的不满意度变化和换道意愿值变化如图18所示,本车在9.84 s时对道路的不满意度大于阈值0.5,此时本车产生换道意图。在结束换道后本车对道路不满意度回落到0.078 7。同时也仿真了基于模糊逻辑和车头时距的微观换道模型,在该模型下车辆在9.4 s下换道意愿值大于随机意愿值因子0.85,此时本车产生换道意图。在结束换道后本车对道路不满意度回落到0.4以下。
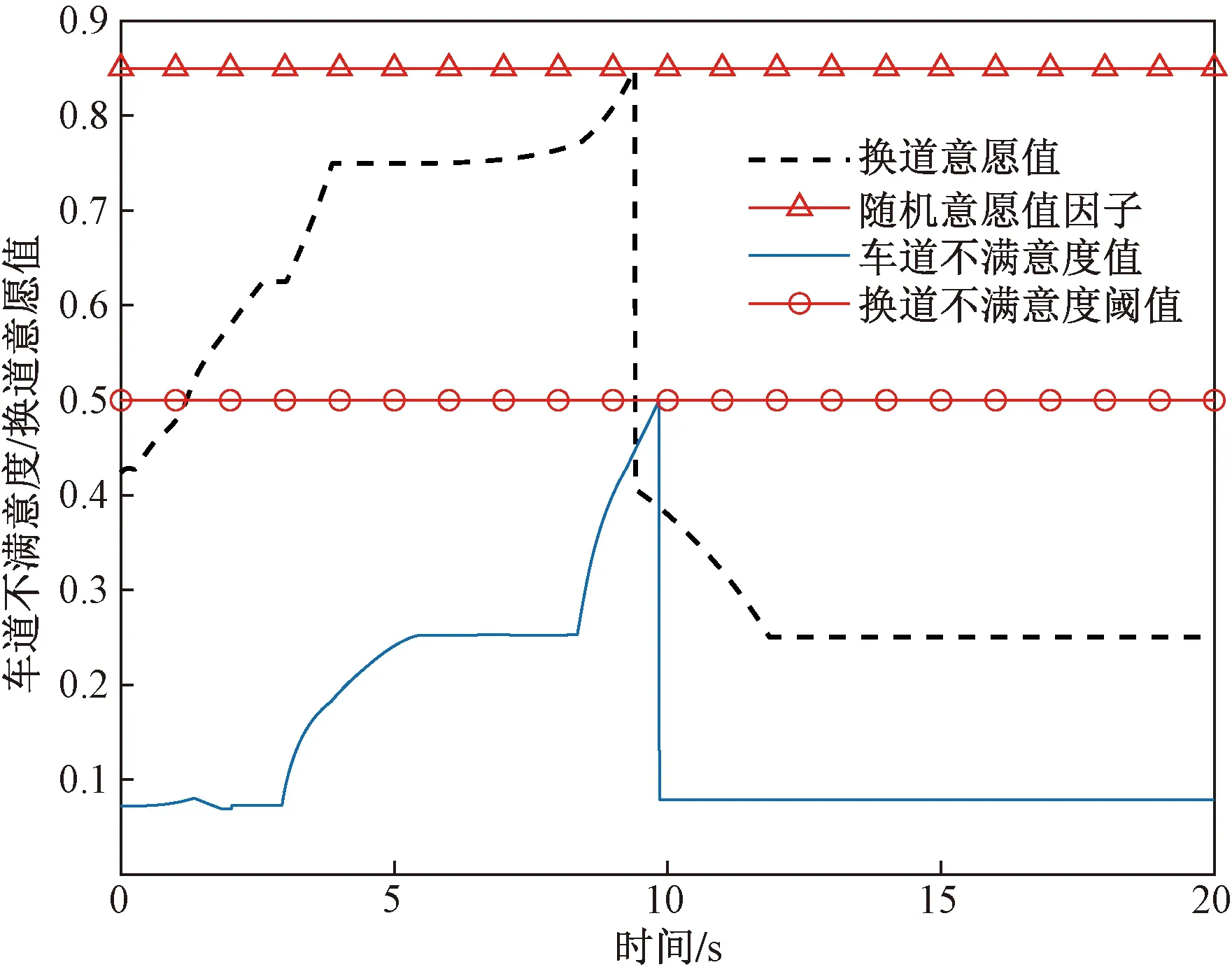
图18 车道不满意度/换道意愿值变化Fig.18 Change in lane dissatisfaction/willingness to change lane values
如图19所示,为本车从原车道换道至邻近车道过程中本车与本车前车的车间距和安全跟车距离的变化。对于本文提出的道路不满意度计算模型,在9.85 s时本车才会主动换道,此时本车与本车前车距离为22 m,安全跟车距离为11.15 m。而对于基于模糊逻辑和车间时距的微观换道模型,本车在9.4 s产生换道意图,此时本车与本车前车距离为23.23 m,安全跟车距离为11.15 m。
3.3 仿真结果分析
结合仿真得到的本车与本车前车间距变化和车道不满意度/换道意愿值变化,本文提出的基于不满意度的换道模型能在整个换道前后使本车与前车间距始终大于安全跟车距离,说明换道决策引擎能在保证跟车安全距离的前提下完成对换道时机的合理判断。相比文献[9]的基于模糊逻辑和车头时距的微观换道模型能在本车与前车还有充足安全的行驶空间下不触发过早的换道意图,故能减少不必要的换道频次,有效提高换道决策的稳定性。
4 结论
(1)以物流载货车为本车对象进行研究,将本车的驾驶工况分为两类,第一类为本车正在按目标车速巡航行驶;第二类为本车需要通过一段加减速过程达到目标车速。针对两类工况可能遇到的换道情况分别设计两套基于模糊决策的车道不满意度计算方法,第一类方法根据本车与前车的安全跟车距离、相对车速、相对车间距离来综合评判本车对车道的不满意度大小。第二类计算方法根据本车与前车的安全跟车距离、相对车速、相对车间距离、相对加速距离来综合评判本车对车道的不满意度大小。
(2)利用本车对本车道和邻近车道的不满意度大小来产生换道意图,在换道意图产生过程中时刻检测本车相对于前车的跟车安全距离与换道安全性距离,保证了本车换道前后的行驶安全。相比大多换道决策,本文不仅考虑换道过程的安全而且也考虑了目标车道和本车道的跟车安全,更具有实际意义。同时本文的模糊换道决策能兼顾安全性和智能性且适用于依目标车速定速巡航、为达到目标车速而加减速等多种复杂工况下换道意图的产生。

