BP神经网络在曲线拟合中的应用

余 苗 陶 婷 陈 佳

(成都理工大学管理科学学院 四川 成都 610059)

曲线拟合是用连续曲线近似地刻画或比拟平面上离散点组所表示坐标之间的函数关系的一种数据处理方法。从一组实验数据(xi,yi)中寻求自变量x和因变量y之间的函数关系 y=f(x)来反映 x和y之间的依赖关系，即在一定意义下最佳地逼近已知数据。

一、曲线拟合原理

二、利用BP网络修改权值

对y=sin(x)曲线实现拟合

(一)训练数据导入

对样本数据的获取，可以通过用元素列表直接输入、创建数据文件、从数据文件中读取等方式。

(二)网络初始化

根据系统输入输出序列，确定网络输入层节点数为1，隐含层节点数为20，输出层节点数为1。初始化输入层、隐含层和输出层神经元之间的连接权值wij，vjk，初始化隐含层阈值t0，输出层阈值t1，给定学习速率a0，a1和u，给定算法迭代次数inum、最大可接受误差error、神经元激励函数sigmoid。

(三)向前输出计算

根据输入变量x，输入层和隐含层间连接权值wij和隐含层阈值t0，计算隐含层输出P：

f为隐含层激励函数，该函数可设置为多种形式，本实验中所选函数为：

根据隐含层输出P，隐含层和输出层间连接权值vjk和输出层阈值t1，计算BP神经网络预测输出Qk：

其中m为输出层节点数，本实验中取1。

(四)权值修正

根据网络预测输入Q和期望输出y，计算网络预测误差e：

ek=yk-Qk

BP神经网络采用梯度修正法作为权值和阈值的学习算法，从网络预测误差的负梯度方向修正权值和阈值。在本实验采用的sigmoid激励函数下，隐含层和输出层间连接权值和输出层阈值更新公式为：

vjk=vjk+u*a1Pjekj=1,2,…,l;k=1,2,…,m

t1k=t1k+u*ekk=1,2,…,m

输入层和隐含层间连接权值和输出层阈值更新公式为：

通过是否达到迭代次数或者错误率是否在可接受范围内来判断算法迭代是否结束，若没有结束，则继续迭代。

三、结论

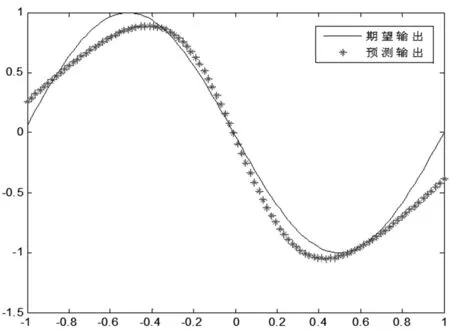
图1 迭代60次拟合

图2 迭代200次拟合

通过上面两个图可以看出，随着迭代次数的增加，预测误差是逐渐减小的，在开始的迭代中，误差减小较快，最后经过规定次数的迭代，基本上能将函数y=sin(x)拟合出来。虽然BP神经网络具有较高的拟合能力，但是预测结果仍然存在一定的误差，其拟合能力也存在一定的局限。