游梁式抽油机变速驱动优化建模与节能机理研究

宋 微 冯子明 张德实，2 于 宁

（1.东北石油大学机械科学与工程学院； 2.大庆油田有限责任公司采油工程研究院； 3.大庆市市场监督管理局）

游梁式抽油机在150多年的发展过程中，经过各种野外苛刻环境的考验，成为了机械采油的主要方式之一。 但是游梁式抽油机存在传动效率低、电动机装机功率高及地下管筒井况复杂等问题，导致其平均效率在国内油田中一直低于30%。

抽油机杆柱载荷的计算最早是在1963年由Gibbs S G首先建立有杆泵一维有阻尼波动方程预测模型，求解得到抽油杆任意位置的位移和应力［1］。1975年，Gibbs S G构建了抽油机井系统运动学和动力学数学模型以及对应的数值求解方法和流程［2］。1983年，Doty D R和Schmidt Z考虑到管筒内的液柱惯性和振动载荷对悬点载荷的影响，建立了杆柱-液柱的二维耦合波动方程， 提高了悬点载荷的预测精度［3］。1989年，余国安和邬示炯针对国内油管一般不锚定的现状， 建立了杆柱-液柱-管柱三维耦合波动方程并提出求解方法，进一步提高了悬点载荷的预测精度［4］。 考虑到高滑差率电动机的转子转速与磁场的不同步性，董世民和马德坤在1996年提出了对应的预测模型和求解方法［5］。 2002年，薛承谨和鲍雨锋采用MacCmark方法解决了电机与抽油机运动和动力耦合的数值算法问题［6］。目前，关于抽油机悬点载荷的动力学模型和求解方法较为完善，为建立主动变速优化控制的机-杆-泵全周期耦合模型、优化方法等提供了理论基础。

最早的抽油机井变速运行是通过间歇采油或改变冲次实现的。 1932年，Coberly C J和Harris F W根据测试的井底压力来控制冲次， 但该方法精度较低而且难以控制［7］。 Gibbs S G根据电机的功率变化来决定泵是否停抽［8］。 Patterson M M建议依据下冲程的第1个1/4时间内的功率来决定是否停抽［9］。Mckee F E通过改变电动机输出电流的频率来改变驱动速度，从而达到提高系统效率的目的［10］。 1995年，Gibbs S G等使用一维波动方程计算泵充满度从而调整冲次的大小，以防止出现泵抽空的现象［11］。 目前，随着控制软件和硬件设备的进步， 出现了全周期实时变速优化控制技术。 2006年，Peterson R G等结合有杆泵控制技术和变速控制技术优化了100口油井， 测试结果显示：100口油井的产量提高范围为10%～160%［12］。Palka K和Czyz J A为了增加油井产量、减载节能，在单个抽汲周期内改变电动机转速［13］。 2011年，Sam G等依据井下动液面深度数据， 使用变速控制技术控制泵速，以保证泵的生产效率［14］。 2015年，Elmer B通过降低下行程速度、 保持上行程速度来减少泵的漏失和提高气锚的分离效率［15］。Carpenter C依据泵充满度提出了变速控制技术，实现了自反馈产量最大化、工况检测及设备保护等功能［16］。2016年，Burgstaller C依据动液面数据，提出了防止抽空和优化产量的方法［17］。 2017年，Alwazeer A等提出变速控制技术， 即通过保持动液面稍高于泵发生空抽时的动液面，来达到优化产量的目的［18］。 Allison A P等提出应用变速控制技术来改善气体对泵的影响［19］。Ferrigno E等结合智能控制技术和遥感系统， 优化设计了50口油井，该技术通过控制电机转速和泵冲次来实现产量和效率的最大化［20］。

通过上述分析可知，有必要建立基于变速控制优化运行的机-杆-泵全耦合动力学模型和求解方法，从而进行变速控制技术的降载节能机理研究以及变速控制下抽油机系统的综合性能分析。

1 抽油机变速运行理论基础

1.1 抽油机运动规律

游梁式抽油机结构尺寸决定了悬点的位移，其中游梁摆动角位移δi和悬点位移S的计算式为：

式中 A——前臂长，m；

ψ——后臂和基杆间的夹角，（°）；

ψb——下死点的ψ角，（°）。

悬点速度v的计算式为：

式中 ω——曲柄角速度，rad/s；

θ——曲柄转角，（°）。

悬点加速度ac的计算式为：

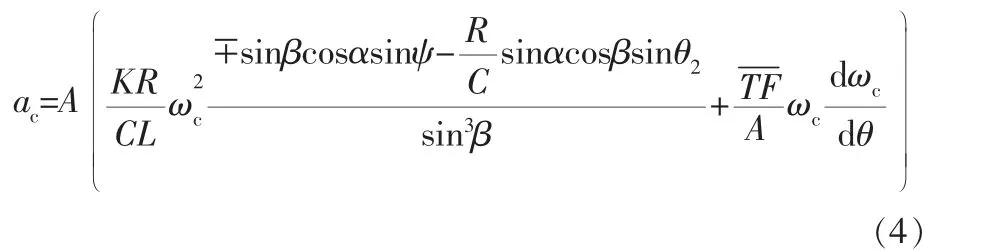
式中 C——游梁后臂长度，m；

K——基杆长度，m；

L——连杆长度，m；

R——曲柄半径，m；

α——曲柄与连杆间夹角，（°）；

β——传动角，（°）；

θ2——曲柄与基杆间夹角，（°）；

ωc——转角速度，rad/s。

1.2 悬点动力学模型

当油井内的油管不锚定时，杆-管-液三维振动方程组如下：

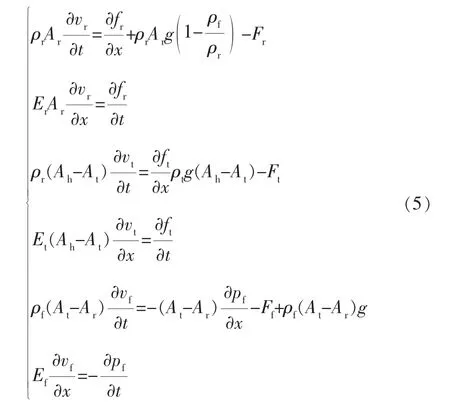
式中 Ah——油管外径面积，m2；

Ar——抽油杆截面积，m2；

At——油管内径面积，m2；

Ef——液柱刚度，N/m2；

Er——抽油杆刚度，N/m2；

Et——油管刚度，N/m2；

fr——杆柱应力，MPa；

ft——管柱应力，MPa；

Ff——液柱受到的阻力，N；

Fr——抽油杆受到的阻力，N；

Ft——油管受到的阻力，N；

g——重力加速度，m/s2；

pf——液柱应力，MPa；

t——时间，s；

vf——液柱速度，m/s；

vr——抽油杆速度，m/s；

vt——油管速度，m/s；

ρf——液柱密度，kg/m3；

ρr——抽油杆密度，kg/m3；

ρt——油管密度，kg/m3。

1.3 抽油机扭矩方程

减速箱输出净扭矩Tnh是光杆扭矩、平衡扭矩和运动件惯性力矩之和，即：

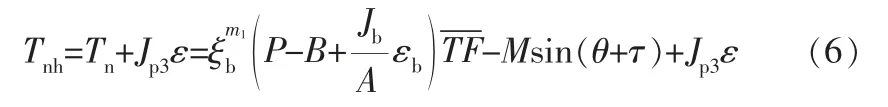
式中 B——不平衡重，kN；

Jb——游梁转动惯量，kg·m2；

Jp3——转动惯量，kg·m2；

M——曲柄平衡扭矩，kN·m；

P——有功功率，kW；

Tn——曲柄轴上阻力矩，kN·m；

τ——偏置角，（°）；

ε——曲柄加速度，m/s2；

εb——游梁摆动角加速度，m/s2；

ξb——四连杆机构的传动效率。

ε由运动微分方程求解。电动机输出扭矩Td的计算式为：

式中 i——抽油机的总传动比；

Jp——电机转动惯量，kg·m2；

m2——指数，Td＞0时m2=1，Td＜0时m2=-1；

ξm——传动效率。

电机转动惯量Jp的计算式为：

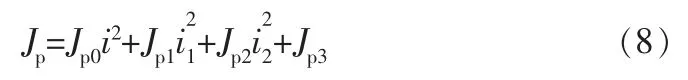
式中 i1——减速器的一级传动比；

i2——减速器的二级传动比；

Jp0——轴上全部转动件的转动惯量，kg·m2；

Jp1——减速器输入轴上折算的转动惯量，kg·m2；

Jp2——减速器中间轴上折算的转动惯量，kg·m2。

2 抽油机变速驱动优化计算流程

以降低电机综合节电率（以匀速拖动计算结果为比较基准）为目标的变速优化目标函数和约

束条件如下：

式中 f（）——计算目标函数的计算函数；

I，Iup，Idown——电动机的输入电流、上冲程和下冲程电流的最大值，A；

k——无功经济当量，一般取0.05～0.08；

n——一个冲次内测试变量的测试点数；

Q——无功功率，kVar；

T——减速箱输出轴扭矩，N·m；

Xi——计算目标函数的相关参数， 如冲程、冲次等；

Y——产量，t/d；

γ——电流平衡度，%，γ=Idown/Iup；

σmax，［σ］——抽油杆实际承受的最大应力、抽油杆的许用应力，MPa。

下标 c——恒速拖动；

e——额定值；

max——最大值。

图1是电动机、抽油机、抽油杆和抽油泵的力学耦合模型求解流程，包括电动机外特性与抽油机运动学、动力学的耦合问题，通过该计算流程可以求解出电动机转速、功率和扭矩，减速箱扭矩，悬点位移、速度、加速度及载荷等参数。

3 案例计算结果优化评价分析

图2是电机转速曲线， 其中蓝色直线代表常规电机转速，红色曲线代表变速曲线，两者在一个周期内的平均速度都是750r/min。 以恒速驱动为对比基准，在进行变速运行评价时，其他所有相关的参数都保持相同。 优化后的电动机转速变化幅度范围是-24.0%～108.6%。 变速优化技术的基本原则是：在一个冲程周期内，重新分布运动件的惯性能量，依据“重载慢驱，轻载快行”的原则，达到降载节能、安全运行的目的。

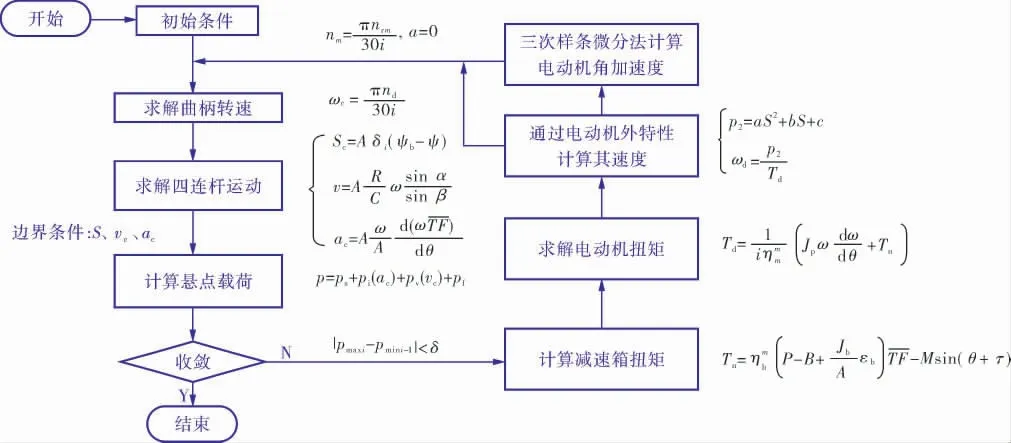
图1 抽油机系统非线性耦合行为预测计算流程

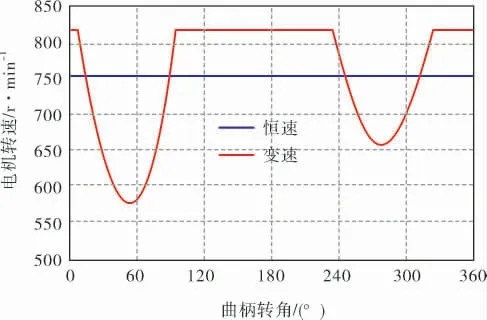
图2 电机转速曲线

图3 悬点位移曲线

图3是两种运行工况下的悬点位移曲线，可以看出变速运行曲线位移峰值点后移，使得上冲程时间较长、下冲程时间较短，可以增加产液进泵时间，提高抽油泵的充满度，尤其是对于稠油；同时悬点载荷缓慢增加，降低了抽油杆受到的强烈交变冲击载荷。 图4是两种运行工况下的悬点速度曲线，可以看出优化后的变速运行曲线具有被“削峰”的特点，在上冲程峰值载荷出现的位置，悬点速度降低，可以降低由于速度引起的动载荷，从而降低峰值载荷。

图4 悬点速度曲线

图5是两种运行工况下的悬点加速度曲线，可以看出变速运行时的悬点加速度峰值明显大于匀速运行时的。 惯性载荷是由加速度引起的。本例中随着加速度的增加，惯性载荷增加，从而降低了抽油杆的峰值载荷。 图6是两种运行工况下的悬点示功图，由图可知变速驱动可以降低悬点载荷， 也降低了示功图中的载荷波动幅度，说明此时的周期载荷系数降低。 本案例的优化目标是提高节电率， 此时的悬点峰值载荷降低率为5.08%，如果以悬点载荷降低率为优化目标，则可以达到10%～20%的预期值。

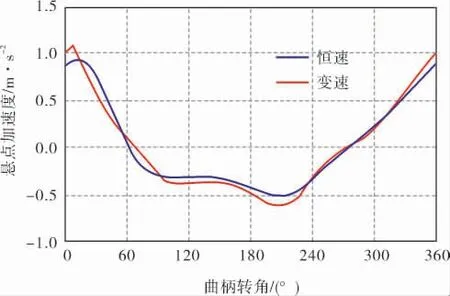
图5 悬点加速度曲线

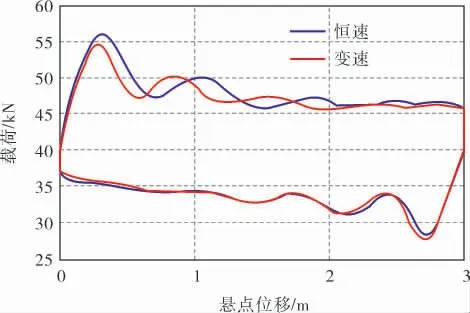
图6 悬点示功图

图7是两种运行工况下的减速箱输出净扭矩，可以看出相比于恒速驱动，变速驱动下的减速箱输出净扭矩大幅减小，特别是曲线的中间部位，扭矩几乎全部消失。 图8是两种运行工况下的电机输出功率，可以看出与恒速驱动相比，变速驱动无论是功率峰值还是负功率都要降低更多，可见在优化后的变速驱动条件下，电动机的实际工作性能获得较大提升。

图7 减速箱输出净扭矩曲线

图8 电机输出功率曲线

表1是两种运行工况下电动机的性能参数及其变化情况， 根据抽油机系统优化结果，37.0kW电动机替换为18.5kW。 平衡度由0.772 2提高到0.926 4，一直保持在合理范围内。 周期载荷系数代表抽油机系统的运行平稳性和承受的交变载荷强度，从1.50降低到1.38，降低了8.00%，说明变速驱动极大地降低了冲击载荷强度，提高了系统运行的平稳性。 电动机的平均有功功率和平均无功功率分别降低了7.36%和31.81%， 说明变速驱动有利于提高电动机的运行效率。 以上数据均说明优化后的变速驱动能够最大程度地发挥电动机在抽油机井系统中的工作效能。

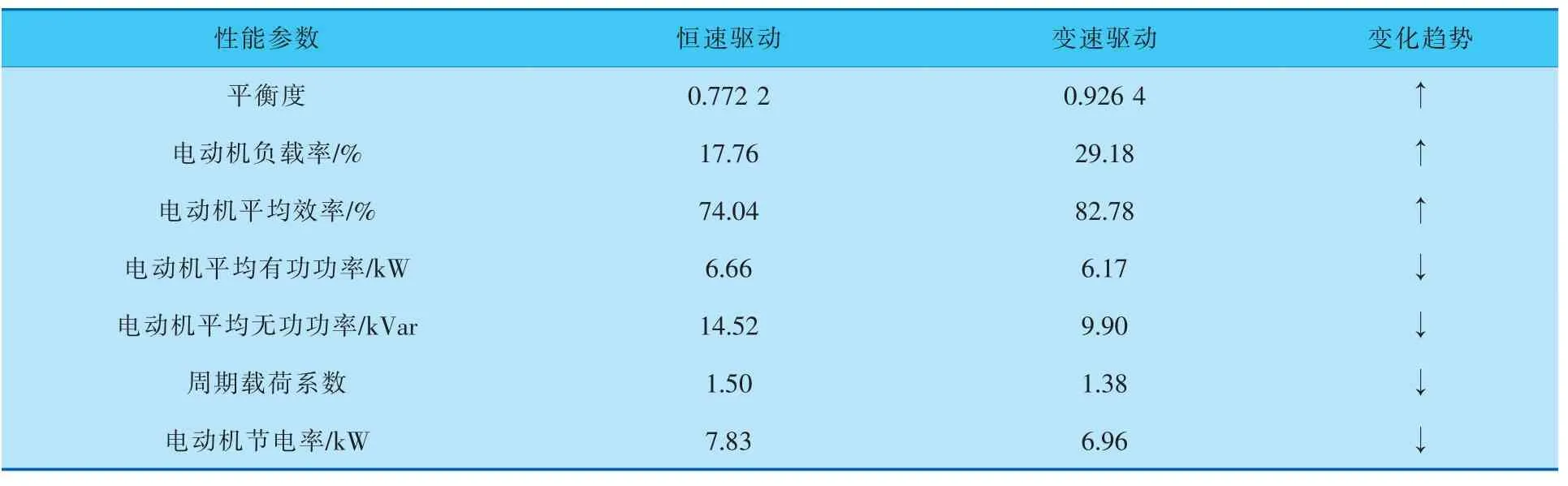
表1 电动机性能参数

将抽油机的恒速驱动变为变速驱动后，依据表2所列的工作特性数值计算出： 电机功率峰值和电机扭矩峰值分别降低了23.85%和9.19%，减速箱输出扭矩峰值降低了8.83%， 悬点载荷峰值降低了2.39%。 虽然这些参数降低幅度不同，但都体现了惯性载荷对电动机的影响要比悬点载荷大这一规律，这也与式（6）～（8）的结果相一致。

表2 抽油机工作特性

4 油田试验

将变速控制技术应用于大庆油田的10口抽油机井上，抽油机类型包括常规抽油机和异相抽油 机（CYJ11-3-48B、CYJY6-2.5-26HB、CYJY14-6-89HF和CYJY10-4.2-53HB）。驱动电机包括三相异步常规电机和多功率电机，额定功率有55、37、37/27、33/50kW。 多数油井含水率在90%以上，冲程范围是1.9～4.2m，冲次范围是2.5～7.5，泵径范围是44～83mm。 总体来说，所选的抽油机井所包含的电动机和抽油机的类型较多，工况范围宽，测试样本数据具有较好的代表性。

10口油井的测试结果表明： 平均节电率为15.8%，说明电动机功率利用率获得大幅提高；功率因数提高了32%， 说明电动机无功功率损耗大幅降低； 效率平均提高2.88%， 说明节能效果明显。悬点峰值载荷由43.7kN降低到42.0kN，泵效从55.1%提高到57.3%，减速箱扭矩峰值平均降低率为16.1%。 可见，变速驱动运行下的电动机、抽油杆柱和抽油泵的工作性能都获得一定程度的提高。

5 结束语

通过对游梁式抽油机的理论分析和实验研究，建立了变速驱动下的抽油机井系统动力模型和求解方法。 提出抽油机变速驱动优化方法：优化目标为节电率最大，约束条件为减速箱和杆柱不过载、产量不降低、平衡良好等，从而建立变速运行优化模型。 同时，提出了抽油机系统变速运行动力耦合行为预测的计算流程，编制的软件可以计算出变速运行时的参数有：电动机的输出功率（包括有功功率、无功功率和视在功率）、输出电流、输出扭矩，减速箱曲柄的角速度、角加速度、扭矩，悬点的位移、速度、加速度、载荷，抽油泵的位移和载荷等。 通过对10口油井测试后的结果表明，变速驱动下的平均节电率为15.8%，减速箱扭矩峰值平均降低率为16.1%， 系统效率平均提高2.88%。