“代表性启发”对初中生古典概率内容学习进阶的影响

何声清

“代表性启发”对初中生古典概率内容学习进阶的影响

何声清

（上海师范大学 数理学院，上海 200234）

以754名七~九年级学生为被试，考查其持有的“代表性启发”对古典概率内容学习进阶的影响机制．结果表明：（1）初中生概率认知中的“代表性启发”随年级递增呈现消退态势；（2）男生持有的“代表性启发”比女生程度更深；（3）学生持有的“代表性启发”与其对古典概率的认知之间存在显著性负相关；（4）“代表性启发”对学生古典概率内容的学习进阶有显著的消极影响，在学生进行概率比较、概率计算时均产生直接干扰．对有效消除“代表性启发”这类不良直觉提出3点建议：（1）仅依靠样本空间概念的学习尚不足以有效消除“代表性启发”；（2）只有掌握了概率的计算法则，学生才可能有效消除“代表性启发”；（3）借助极端案例帮助学生造成认知冲突，引导其在概率决策时摒弃主观臆断．

代表性启发；古典概率；样本空间；学习进阶；中介效应

1 问题提出

概率素养（probability literacy）日渐成为大数据时代世界公民必备的一项数学素养[1]，例如Freudenthal数学教育研究所所长Lange在梳理“数学素养”概念谱系时就明确将“不确定性”纳入其中[2]．自20世纪80年代以来，诸如美国、加拿大、澳大利亚等欧美国家的教育部门陆续将概率内容纳入基础教育阶段的课程标准之中[3]．中国教育部于2001年颁布的《全日制义务教育数学课程标准（实验稿）》也首次让概率内容“飞入寻常百姓家”[4]，并于2012年颁布的《全日制义务教育数学课程标准（2011年版）》中进一步调整了其在各学段的认知要求[5]．

中小学阶段的概率内容主要涉及古典概率（classic probability）和频率概率（frequentist probability），其中古典概率是从理论出发的概率，它要求学生在理解随机性概念的基础上构造样本空间进而进行概率计算、概率比较等．Jones等人提出了一个描述儿童古典概率概念的发展框架，将该内容解构为样本空间、事件的概率、概率比较及条件概率4个维度[6]．这不仅得到了国内新近研究的支撑[7]，事实上当前国际范围内的中小学数学教材对于该部分内容也大都有类似的解构[3]．例如，美国《共同核心州立标准》（，简称CCSSM）在七年级的课程目标中明确提出“学会利用列表、树形图等手段计算复合事件的概率；理解复合事件中的样本空间，并将其应用到概率计算当中”．

从学习进阶的逻辑来看，对随机性概念的学习应走在古典概率知识链的最前端，即首先要厘清必然事件和随机事件．其次，学生需要认识等可能性和样本空间的概念，即能够弄清随机试验所有可能的结果．最后，学生才能够据此进行概率计算、概率比较等．事实上，上述学习进阶假设也得到了已有研究的支撑．张增杰等人开展的“5~15岁儿童掌握概率概念的实验研究”表明：儿童的概率概念是按照“理解可能性→认识样本空间→认识概率的相对大小→概率大小的定量化”的步次向前推进的[8-9]．但也有新近的研究表明：理解样本空间对儿童而言并非易事[10]，他们的概率概念更倾向于从“定性感知”向“定量计算”发展，即按照“认识随机性→定性认识概率的相对大小→概率大小的整数表征→认识样本空间→概率大小的分数表征”这一宏观序列逐步进阶[11]．然而事实上，学生概率内容的学习进阶并非总是如此顺畅．他们在接触学校的概率课程前，已然具备了有关概率的非正式知识（informally acquired knowledge），这些非正式知识或多或少地影响他们对正式课程的学习[12]．因此即便在上述知识链中，儿童概率概念的学习进阶也会不可避免地受到不良直觉或错误观念的影响．

“代表性启发”（representativeness heuristic）就是学生概率认知过程中的一个典型错误观念[13-15]，这也得到了新近数学教育领域研究的证实[16]．Kahneman与Tversky较早地将“代表性启发”界定为：人们在概率决策时常常从结果的特征出发，倾向于认为具有与“母体”（parent population）相似特征的结果更容易发生[17]．例如在“抛硬币”试验中，若前5次抛出的结果都是“正面”，有人会认为第6次抛出的结果更可能是“反面”，因为他们倾向于认为“正正正正正反”比“正正正正正正”更具有“一般性”．再例如，从装有1个黑球和3个白球的不透明盒子里同时摸出2个球，有人会认为“1个黑球和1个白球”这种“混合结果”更加具有“一般性”，而“两个恰好都是白球”则显得十分“极端”或“特殊”，因此摸出前者的概率更大．新近一项有关学生概率比较策略的研究表明：在古典概率问题情境中，学生并非总是如预期那样——即通过构造样本空间来计算概率并据此进行概率比较，而是常常会诉诸各类不良直觉进行决策[18]．这在上述两个案例中也可见一斑．

那么，“代表性启发”对学生古典概率内容的学习进阶有多大程度的影响？影响机制是什么？研究着眼于上述两个问题的探索，以期为古典概率内容的教学提供有益参考．

2 研究设计

2.1 被试

采用分层随机取样，从山东省青岛市办学水平为“优秀”“良好”及“一般”的3所学校抽取七~九年级被试共754名，其中七、八及九年级被试分别为276名、243名及235名，男生、女生分别为376名和375名（缺失3名被试性别信息）．

2.2 测查材料

2.2.1 古典概率测试

测试共涉及5个“摸球”问题．问题情境均是“在一个不透明的盒子里，有×个黑球、×个白球、×个绿球，它们除颜色外均相同．闭上眼睛，从盒子里同时摸出2个球”．之所以不再设计“摸出1个球”的问题，是由于高年级学生在该情境中的作答大都良好，常常出现“天花板效应”[19]．借鉴前研究的经验，一方面通过控制“球的个数”“颜色种类”等变量对问题进行递进设置[20]，一方面针对每个问题设计进阶式的概率任务[11]．具体而言，每个问题均涉及3个不同的概率任务：T1考查学生对样本空间的认知，T2考查学生对概率大小的定性比较，T3考查学生对概率大小的定量计算．需要特别指出的是：第一，研究者并未设计有关条件概率的任务．其原因在于，国内外的中小学数学教材鲜有触及这一内容，并且实证研究也已然表明它对于中小学生而言难度颇大[21]．第二，研究者并未设计有关随机性概念的任务．其原因在于，在“摸球”游戏等概率问题中，中学生对于随机性概念的理解已然达到颇高水平[19]．另需补充说明的是，尽管“样本空间”的书面概念在高中时才正式提及，但初中教材中“用列举法求概率”等内容已然涉及到这一概念，只是未明确提及概念术语而已．

从知识逻辑上看，学生的概率概念是在“样本空间→概率计算→概率比较”的序列中进阶的．以Q2为例，学生首先需要明晰摸出2个球的结果共有6种（任务1），即{两个白球、两个黑球、黑1白1、黑1白2、黑2白1、黑2白2}，它也叫做“基本事件”；其次需要分别计算“2个白球”和“1个黑球和1个白球”的概率（任务3），即两者的概率分别为1/6和4/6；最后根据上述计算结果，对两者的概率进行比较（任务2）．

值得提及的是，以往研究表明：学生在T1中常常遇到困难，原因一方面在于他们缺乏必要的组合知识[22]，一方面在于他们对基本事件的概念缺乏认识[20]．仍以Q2为例，其基本事件为“黑1白1、黑1白2、黑2白1、黑2白2、黑1黑2、白1白2”，但以往研究表明：若不事先对各球进行标记，有92.6%的初中生会认为“摸出2个球”共有3种可能的情况，即“1个黑球和1个白球、2个白球、2个黑球”．尽管在给出上述作答的学生中，有11.1%的学生能够列举所有可能的结果——只是在作答时未对其做出区分，但学生构造样本空间的能力总体并不乐观[23]．鉴于上述考虑，为避免被试受到不必要干扰，研究者在任务设计时对插图中相同颜色的球进行了标记．事实上，中国初中教材在“概率初步”内容设计时也作此处理[24]．任务设计详见表1．

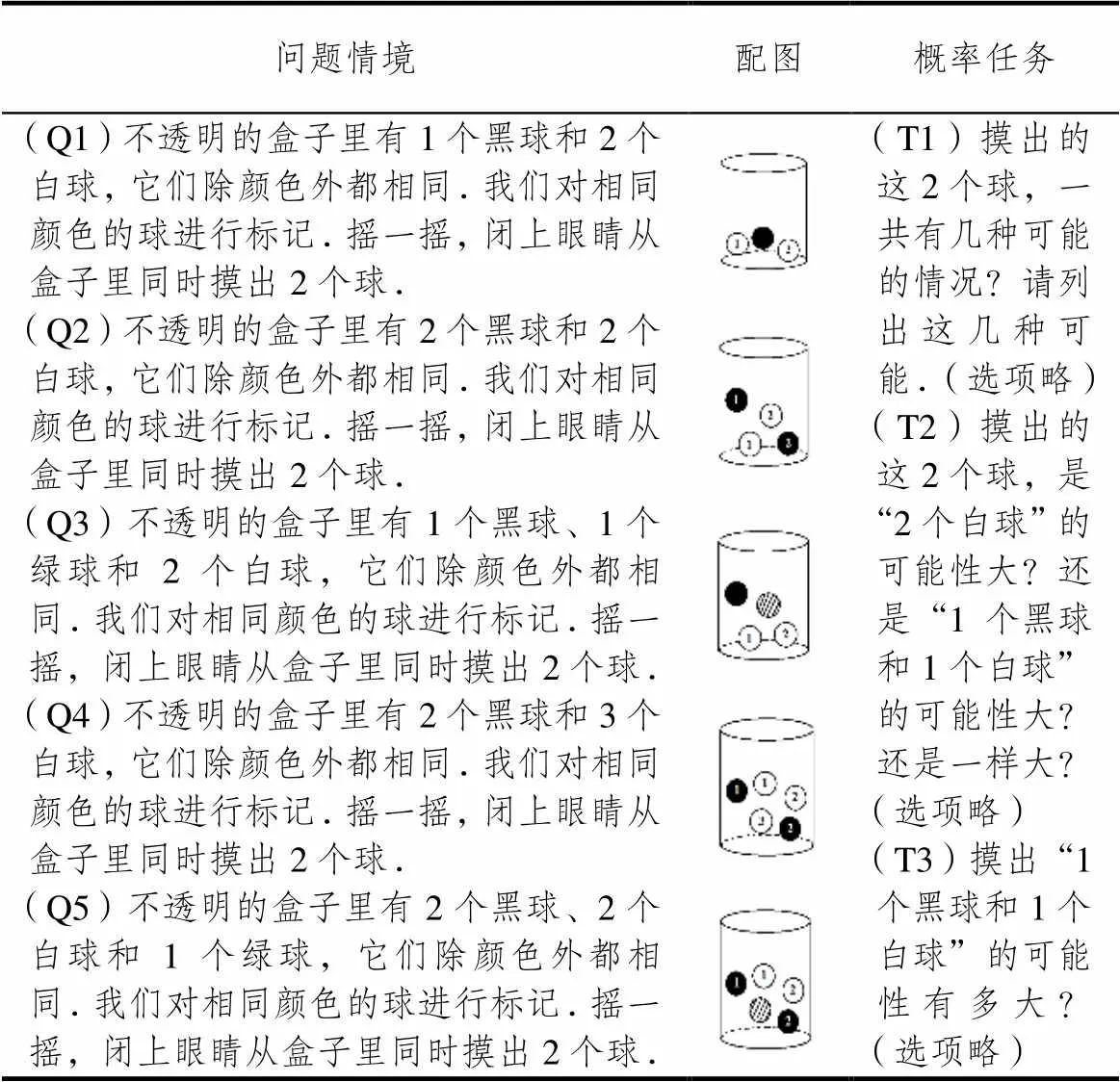
表1 古典概率测试的任务设计

2.2.2 “代表性启发”问卷

“代表性启发”问卷共设置了3个问题．采用5级Likert量表形式，被试根据问题描述对其认可程度进行评估．层级“1”~“5”按程度递增依次表示“完全不同意”~“完全同意”．以Q1为例：

美国的Kelly太太先后生了6个孩子，她先后生出“男孩、女孩、女孩、男孩、女孩、男孩”的可能性比先后生出“男孩、男孩、男孩、男孩、女孩、男孩”的可能性更大．

持有“代表性启发”的被试通常会认为前者的概率更大，因为“它看上去似乎更具有一般性：一方面，男孩和女孩个数相当；另一方面，两个性别的出生顺序没有明显的规律，且不存在连续生出某个性别的极端情况”．被试认可程度越高表明其“代表性启发”这一不良直觉程度越深．

2.2.3 信度

2.3 研究方法

在数据收集阶段，采用调查法进行古典概率测试和“代表性启发”测试，采用访谈法对个别被试进行事后访谈．在数据分析阶段，首先采用相关分析初步厘清关涉变量间的关系，其次采用路径分析对“代表性启发”在学生古典概率内容学习进阶中的影响机制进行深入探索．

2.4 研究假设及模型建构

如前文所述，若从知识逻辑来看，学生的概率概念是在“样本空间→概率计算→概率比较”的序列中进阶的．就研究所涉及的测查问题而言，在上述学习进阶过程中，“代表性启发”对于学生样本空间概念学习的理论上影响不大：因为学生构造样本空间时主要依赖其组合知识的发展．在概率计算和概率比较任务中，学生持有的“代表性启发”则对学生的作答存在潜在影响：学生有可能放弃理论推演和计算策略，转而诉诸“代表性启发”做出决策．仍以Q2为例，即便学生在T1中能够正确构造样本空间，但在T2中常常却会做出“因为摸出的2个球都是白球太难了，摸出黑白搭配更加容易”的判断．鉴于以上假设，将“代表性启发”作为影响概率比较和概率计算的中介变量，分别构建如下模型：

模型1．将“样本空间”作为影响“概率比较”的直接变量（），将“代表性启发”作为影响“概率比较”的中介变量（）．“样本空间”对“概率比较”的直接效果（→）记为；“样本空间”对中介变量的直接效果（→M）记为；中介变量对“概率比较”的直接效果（→）记为．

模型2．将“样本空间”作为影响“概率计算”的直接变量（），将“代表性启发”作为影响“概率计算”的中介变量（）．“样本空间”对“概率计算”的直接效果（→）记为；“样本空间”对中介变量的直接效果（→）记为；中介变量对“概率计算”的直接效果（→）记为．

模型3．将“概率计算”作为影响“概率比较”的直接变量（），将“代表性启发”作为影响“概率比较”的中介变量（）．“概率计算”对“概率比较”的直接效果（→）记为；“概率计算”对中介变量的直接效果（→）记为；中介变量对“概率比较”的直接效果（→）记为．

对于上述模型均有：

3 结果与分析

3.1 初中生概率认知中“代表性启发”的表现

对各年级学生概率认知中“代表性启发”的表现进行描述性统计．结果显示：七~九年级学生“代表性启发”的得分随年级递增逐级降低（七年级=2.58，=1.05；八年级=2.29，=1.05；九年级=2.03，=0.98）．Welch (2, 497.003)=18.722，＜0.001，表明不同年级间“代表性启发”的得分存在显著性差异．Dunnett T3多重比较显示，各年级学生“代表性启发”得分差异显著（Δ七年级-八年级=0.29，＜0.01；Δ七年级-九年级=0.55，＜0.001；Δ八年级-九年级=0.26，＜0.05）．表明随年级递增，初中生概率认知中的“代表性启发”呈消退态势．

对不同性别学生“代表性启发”得分进行描述性统计．结果显示：男生“代表性启发”得分高于女生（男生=2.40，男生=1.08；女生=2.24，女生=1.01；Δ男生-女生=0.16），且上述差异达到显著（=2.187，＜0.05，Cohen’s=0.153）．

3.2 关涉变量的描述性统计及相关分析

若不考虑人口学变量“性别”，学生“代表性启发”的得分与其3个概率任务的得分之间均存在显著性负相关（-0.261≤≤-0.211；所有＜0.001），学生3个概率任务的得分两两之间均存在显著性正相关（0.497≤≤0.747；所有＜0.001），这符合理论预期和研究的假设．此外，学生性别与“代表性启发”之间存在显著性负相关（=-0.08，＜0.05），与各个概率任务得分之间均存在显著性正相关（0.098≤≤0.127，所有＜0.01），在后续分析中将其作为控制变量．关涉变量的均值、标准差及相关系数详见表2．

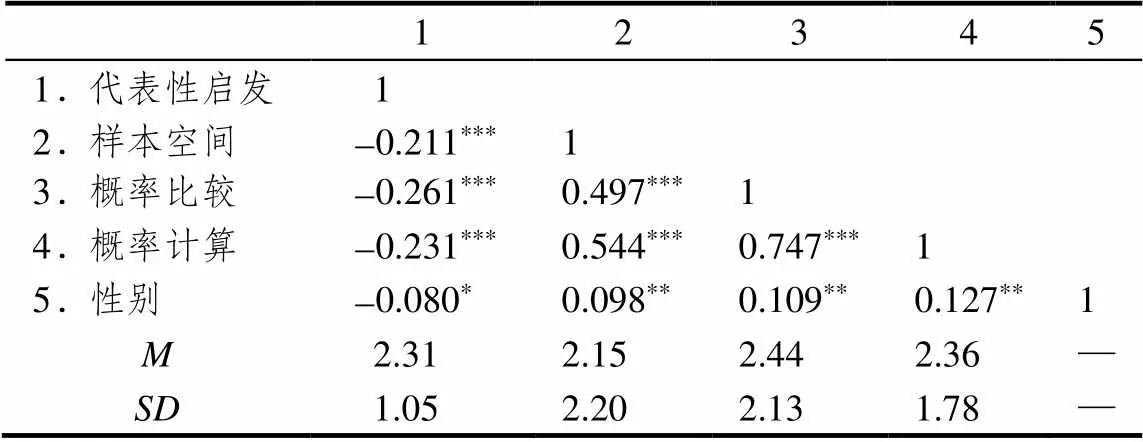
表2 关涉变量的均值、标准差及相关系数

注：*表示＜0.05，**表示＜0.01，***表示＜0.001

3.3 “代表性启发”对初中生古典概率内容学习进阶的影响机制

（1）“代表性启发”在“样本空间→概率比较”进阶序列中的中介效应．

以性别为控制变量，以“样本空间”为自变量，以“代表性启发”为中介变量，以“概率比较”为因变量，采用Bootstrap方法重复抽样5 000次进行回归系数的显著性检验，模型的标准化系数及其显著性指标如表3所示．

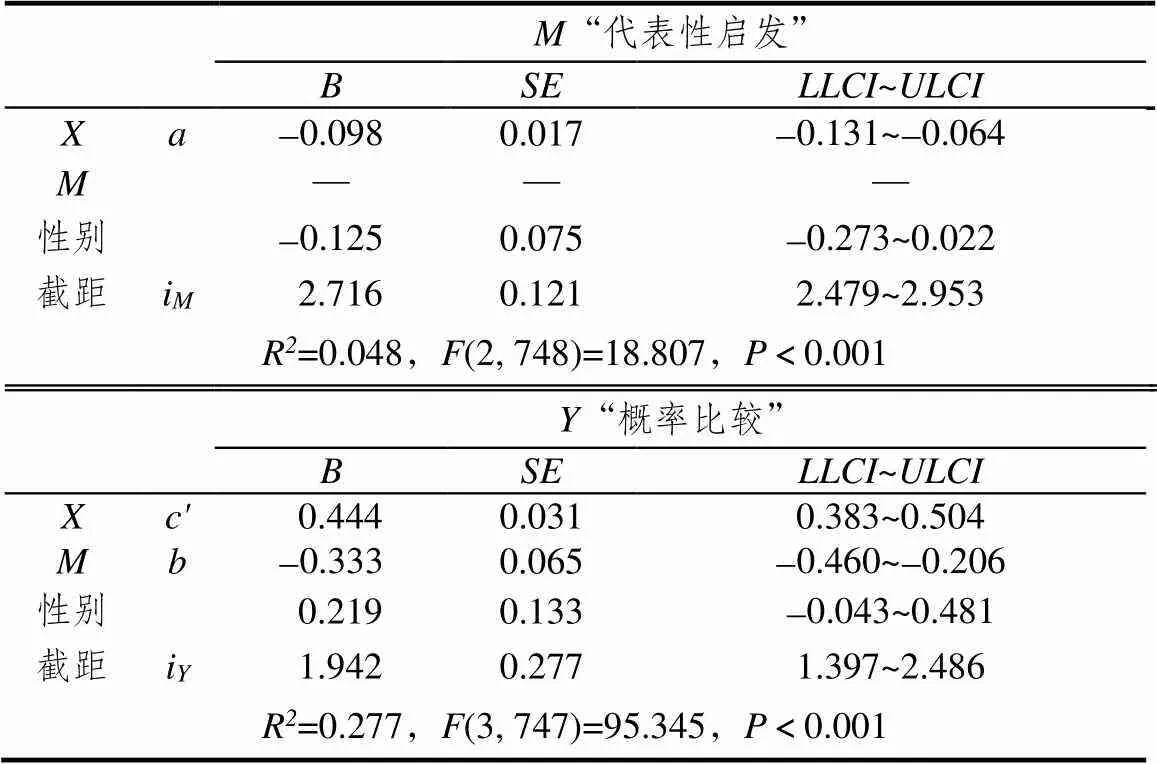
表3 模型1中“代表性启发”的中介效应分析

注：表示“样本空间”

“样本空间”对“代表性启发”有显著的直接负向影响（=-0.098，-0.131≤≤-0.064），对“概率比较”有显著的直接正向影响（=0.444，0.383≤≤0.504）；“代表性启发”对“概率比较”有显著的直接负向影响（=-0.333，-0.460≤≤-0.206）；“样本空间”通过“代表性启发”对“概率比较”有间接的正向影响，且达显著（=0.032，0.018≤≤0.052）；“样本空间”对“概率比较”的直接影响效应量为93.2%，通过“代表性启发”对“概率比较”的间接影响效应量为6.8%；该模型能够解释因变量25.1%的变异（＜0.001），总体效果达到显著（=0.476，0.416≤≤0.537）．

（2）“代表性启发”在“样本空间→概率计算”进阶序列中的中介效应．

以性别为控制变量，以“样本空间”为自变量，以“代表性启发”为中介变量，以“概率计算”为因变量，采用Bootstrap方法重复抽样5 000次进行回归系数的显著性检验，模型的标准化系数及其显著性指标如表4所示．

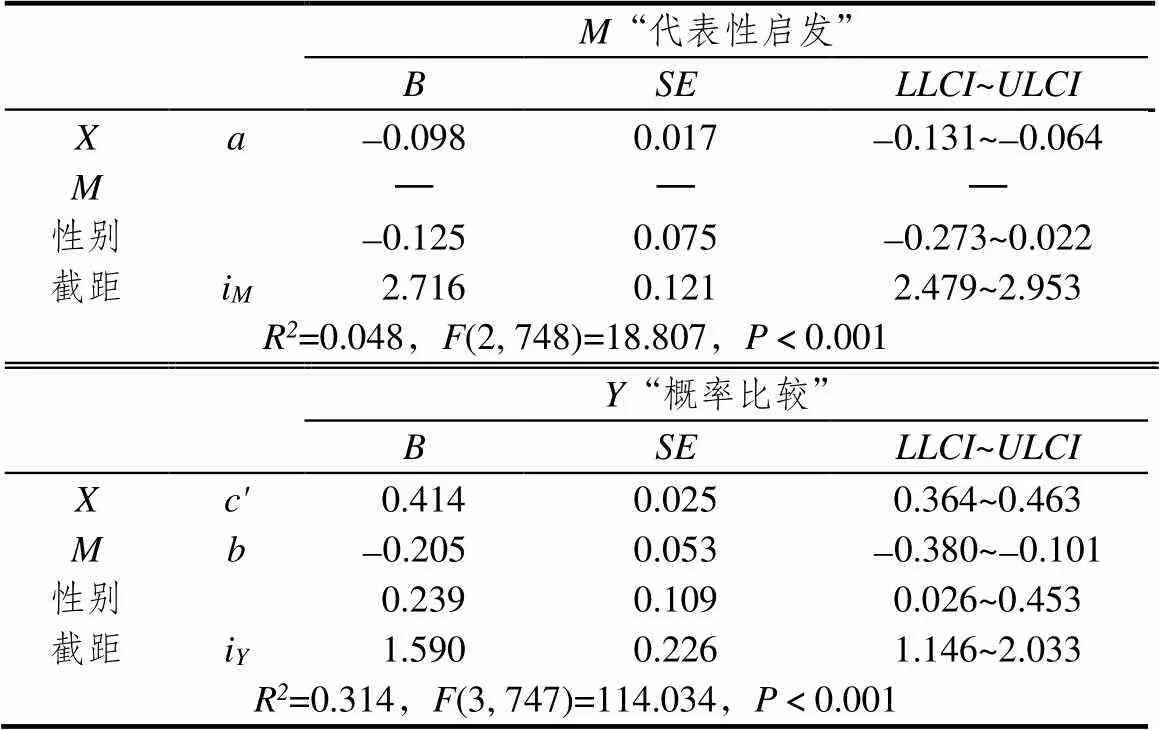
表4 模型2中“代表性启发”的中介效应分析

注：表示“样本空间”

“样本空间”对“代表性启发”有显著的直接负向影响（=-0.098，-0.131≤≤-0.064），对“概率计算”有显著的直接正向影响（=0.414，0.364≤≤0.463）；“代表性启发”对“概率计算”有显著的直接负向影响（=-0.205，-0.380≤≤-0.101）；“样本空间”通过“代表性启发”对“概率计算”有间接的正向影响，且达显著（=0.020，0.009≤≤0.033）；“样本空间”对“概率计算”的直接影响效应量为95.4%，通过“代表性启发”对“概率计算”的间接影响效应量为4.6%；模型能解释因变量30.0%的变异（＜0.001），效果显著（=0.434，0.385≤≤0.483）．

（3）“代表性启发”在“概率计算→概率比较”进阶序列中的中介效应．

以性别为控制变量，以“概率计算”为自变量，以“代表性启发”为中介变量，以“概率比较”为因变量，采用Bootstrap方法重复抽样5 000次进行回归系数的显著性检验，模型的标准化系数及其显著性指标如表5所示．

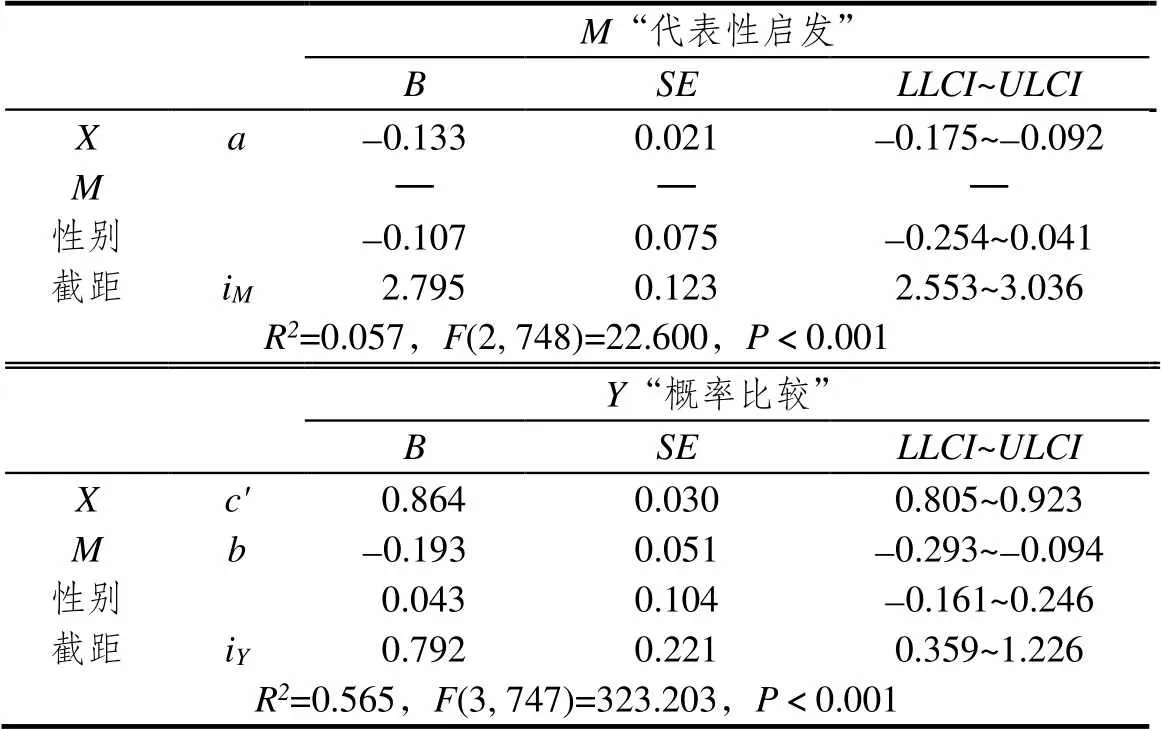
表5 模型3中“代表性启发”的中介效应分析

注：表示“概率计算”

“概率计算”对“代表性启发”有显著的直接负向影响（=-0.133，-0.175≤≤-0.092），对“概率比较”有显著的直接正向影响（=0.864，0.805≤≤0.923）；“代表性启发”对“概率比较”有显著的直接负向影响（=-0.193，-0.293≤≤-0.094）；“概率计算”通过“代表性启发”对“概率比较”有间接的正向影响，且达显著（=0.026，0.011≤≤0.044）；“概率计算”对“概率比较”的直接影响效应量为97.1%，通过“代表性启发”对“概率比较”的间接影响效应量为2.9%；模型能解释因变量55.6%的变异（＜0.001），效果显著（=0.890，0.832≤≤0.947）．

3.4 “代表性启发”对初中生古典概率内容学习进阶的影响机制质性分析

以Q2为例，对某被试进行了访谈．该被试在古典概率测试中的作答表现是：在所有问题的T2中均选择“摸出‘1个黑球和1个白球’的可能性大”．

【访谈片段1：“代表性启发”对被试概率比较任务的消极影响】

师：第二问，你认为“‘1个黑球和1个白球’的可能性大”，能具体说一说理由吗？

生：因为我感觉黑白配概率更大．

师：你怎么知道黑白配概率最大？

生：只有黑白配是两种颜色都有的，盒子里有黑球也有白球，摸到两个都是黑的或者摸到两个都是白的，都不太

合适．

师：你为什么会用“合适”这个词？

生：（无作答）

师：我是说，你之所以认为这个（摸到“1个黑球和1个白球”）概率大，那个（摸到“2个黑球”）概率小，是看哪个结果符合你心理的预期？

生：也不是心理的预期吧．就是感觉这种黑白球都有更像现实．

师：我大概明白你的意思了．我重复一下你的意思：你觉得摸到两个黑球这种情况比较极端、比较难，而摸到一黑一白似乎比较容易，因为它不是那种极端的结果，对吗？

生：（思考片刻）差不多是的．

【分析】被试在T2中认为摸到“1个黑球和1个白球”的可能性更大．从给出的理由来看，该被试在概率比较时持有“代表性启发”这一错误观念，并且被试认为摸到这种混合结果更加“合适”或“更像现实”，上述观点也得到了进一步的确认．综上可见，该被试在概率比较时陷入了“代表性启发”的迷雾，诉诸于一套自认为合理的“法则”．

【访谈片段2：借助直观图示引导被试寻求可靠策略】

师：老师给你讲讲解题过程，你看看有没有道理．（在稿纸画出Q2的插图）你看这个图，现在你想象一下：摇一摇盒子，闭上眼睛从中同时摸出两个球．老师觉得，有可能摸到1号黑球和1号白球（画示意图），有可能摸到……总的来说，摸到“1个黑球和1个白球”有4种可能的搭配．

生：明白．

师：也就是说，理论上有4种搭配都是“1个黑球和1个白球”，而只有一种搭配是“2个白球”．对吗？

生：对的．

【分析】研究者借助直观示意图向被试详细列举了摸球的所有可能结果，并向其强调了摸出“1个黑球和1个白球”实则包含了其中的4种结果．被试对此表示认同．

【访谈片段3：“代表性启发”的消除及其对概率比较的积极影响】

师：老师再给你看一个例子．（边画插图边解释题意）盒子里有1个黑球和3个白球，共4个球．还是一样，摇一摇盒子，闭上眼睛从中同时摸出两个球．你认为摸到“2个白球”和“1个黑球和1个白球”哪个可能性大？

生：（思考片刻）一样大．（画示意图）摸到“2个白球”可以是这两个，也可以是……摸到“1个黑球和1个白球”可以是这两个，也可以是……它们都是3种情况，所以概率一样大．

师：再来看一个题目．（边画插图边解释题意）盒子里有1个黑球和99个白球，共100个球．还是一样，摇一摇盒子，闭上眼睛从中同时摸出两个球．你认为摸到“2个白球”和“1个黑球和1个白球”哪个可能性大？

生：两个白球，白球太多了．

师：你的“黑白配”还管用吗（原意是：你还认为一黑一白这种“黑白配”的概率更大吗）？

生：不管用了．

师：我给你解释一下原因吧．首先摸到“1个黑球和1个白球”一共有……

生：99种情况．

师：摸到“2个白球”呢？

生：（努力思考）

师：这个你还没学过，算起来比较难．但是你可以想象，摸到“1个黑球和1个白球”说明肯定要有黑球被摸到，对吧？100个球里只有1个黑球，摸到它谈何容易？

生：对的．

【分析】为了更彻底地纠正被试持有的“代表性启发”，研究者临时设计了两个极端案例以进一步引起认知冲突．被试能够仿照研究者提供的策略，即借助“标记法”构建样本空间，并在此基础上对两者的概率进行比较，最终否定了自己之前持有的“代表性启发”．尽管最后一个问题对于被试而言难度过大，但被试最终还是意识到了其持有的“代表性启发”并不可靠．可见，上述两个案例对纠正学生的“代表性启发”初见成效．

4 讨论与建议

4.1 初中生概率认知中的“代表性启发”随年级递增呈现消退态势

人们对于概率概念的不良直觉常常十分顽固．诸多研究一再表明：无论是学龄前儿童[25]、小学生[26]、中学生[27]等青少年群体，亦或是大学生[28]、教师[29]等成人群体，他们在概率决策时大都表现出不同程度的不良直觉．Garfield在其研究中更明确地指出：关于概率的不良直觉在不同年龄层之间广泛存在且十分顽固[30]．新近的研究也表明：初中生对于概率概念的不良直觉通常随着年级的递增呈现此消彼长的发展态势，有的能够逐渐消除（例如“认为概率无法量化”），有的则十分顽固（例如“等可能性偏见”）[31]．研究则进一步表明：对于初中生而言，他们概率认知中的“代表性启发”一般会随着年级的递增呈现消退态势．关于它是否会在高中阶段得到更彻底的消除，尚待进一步的研究．

4.2 “代表性启发”是影响学生古典概率内容学习进阶的关键变量

研究发现，学生持有的“代表性启发”与其对古典概率的认知之间存在显著性负相关（＜0.001），其中与“概率比较”的负相关最强（=-0.261），与“概率计算”的负相关次之（=-0.231），与“样本空间”的负相关最弱（=-0.211）．作为中介变量，“代表性启发”显著地阻碍了学生古典概率内容的学习进阶．具体而言，“代表性启发”在“样本空间→概率比较”进阶序列中对“概率比较”的直接负向影响最强（=-0.333），在“样本空间→概率计算”进阶序列中对“概率计算”的直接负向影响次之（=-0.205），在“概率计算→概率比较”进阶序列中对“概率比较”的直接负向影响略弱（=-0.193）．以上说明，“代表性启发”在学生古典概率内容学习进阶中，主要阻碍了学生概率比较的能力：第一，学生在面临概率比较任务时，他们很容易陷入“代表性启发”的迷雾，主观地将其视作合理的“法则”；第二，即便学生能够构造样本空间，但在面临概率比较任务时依然有可能诉诸“代表性启发”这类不良直觉；第三，即便学生能够进行概率计算，但在面临概率比较任务时也有可能忽视上述量化结果转而基于“代表性启发”加以判断．值得提及的是，“代表性启发”甚至对于学生的概率计算也会造成消极影响：即便他们能够构造样本空间，但在概率计算时也有可能放弃可靠策略转而诉诸“代表性启发”．

4.3 消除学生“代表性启发”不良直觉的建议

“代表性启发”是学生概率概念学习过程中表现出的一类典型不良直觉．尽管它随着年级的递增有所消除，但在教学中彻底消除它依然任重而道远．结合定量和定性两方面的分析，研究者对有效消除“代表性启发”这类不良直觉提出如下建议．

第一，仅仅依靠样本空间概念的学习尚不足以有效帮助其消除“代表性启发”．学生样本空间概念的加深仅仅能够微弱地消除其持有的“代表性启发”，但“代表性启发”对于学生概率比较和概率计算能力的消极影响则显然强烈得多．具体而言，在“样本空间→概率比较”进阶序列中，“样本空间”对“代表性启发”的路径系数仅为-0.098，而“代表性启发”对“概率比较”的路径系数则高达-0.333；“样本空间”通过“代表性启发”对“概率比较”的路径系数仅为0.032，该间接影响路径的效应量仅为6.8%．在“样本空间→概率计算”进阶序列中，“样本空间”对“代表性启发”的路径系数仅为-0.098，而“代表性启发”对“概率计算”的路径系数则高达-0.205；“样本空间”通过“代表性启发”对“概率计算”的路径系数仅为0.020，该间接影响路径的效应量仅为4.6%．

第二，只有当学生掌握了概率的计算法则时，他们才可能有效地纠正其持有的“代表性启发”．在“概率计算→概率比较”进阶序列中，“概率计算”对“代表性启发”的路径系数为-0.133，这明显高于前两个进阶序列中“样本空间”对“代表性启发”的路径系数．通过比较模型1和模型3也可发现：模型1中“样本空间”对“概率比较”的路径系数为0.444，模型3中“概率计算”对“概率比较”的路径系数则高达0.864；模型1中“样本空间”对“概率比较”的总体路径系数为0.476，模型3中“概率计算”对“概率比较”的总体路径系数则高达0.890；模型1能够解释因变量25.1%的变异，模型3则能够解释因变量55.6%的变异．以上说明，只有当学生能够真正进行概率计算时——这意味着他们不仅能构造样本空间，还能基于样本空间求概率——他们才有可能有效地纠正其持有的“代表性启发”，也才有可能在进行概率比较时彻底摆脱该类不良直觉．

第三，借助极端案例帮助学生造成认知冲突，引导其在概率决策时摒弃主观臆断．学生在面临概率计算、概率比较等问题情境时常常放弃理论推演，转而诉诸主观臆断或寻求一套“自认为合理的规则”．例如，“代表性启发”这类不良直觉与“中庸思维”似有异曲同工之处[32-40]，学生在概率决策时信奉着“摸出黑白配更有一般性，两个都是白球则显得十分极端”这样的“法则”．在实际教学中，访谈资料中的两个极端案例不妨一试：如果盒子里有1个黑球和3个白球，摸出“1个白球和1个黑球”的概率仍然更大吗？如果盒子里有1个黑球和99个白球，摸出“1个白球和1个黑球”又谈何容易？这时候引导学生反思：类似于“黑白配概率更大”的解释是否显得苍白无力了呢？

5 研究结论

（1）初中生概率认知中的“代表性启发”随年级递增呈现消退态势；男生持有的“代表性启发”比女生程度更深．

（2）“代表性启发”与概率认知间均存在显著性负相关．

（3）“代表性启发”对学生古典概率内容学习进阶有显著的消极影响，尤其在学生进行概率比较时产生的直接阻碍最强．

（4）样本空间概念的加深仅能微弱地消除其持有的“代表性启发”，但“代表性启发”对概率比较和概率计算能力的消极影响则显然强烈得多．只有当学生掌握了概率的计算法则时，他们才可能有效地纠正其持有的“代表性启发”．

（5）上述结论也得到了访谈资料的支撑．

[1] NILSSON P, LI J. Teaching and learning of probability [M] // CHO S J. The proceedings of the 12th international congress on mathematical education: intellectual and attitudinal challenges. New York: Springer, 2015: 437-442.

[2] LANGE J. Mathematical literacy for living from OECD-PISA perspective [J]. Tsukuba Journal of Educational Study in Mathematics, 2006 (10): 25.

[3] 曹一鸣．十三国数学课程标准评价（小学初中卷）[M]．北京：北京师范大学出版社，2012：446-451．

[4] 中华人民共和国教育部．全日制义务教育数学课程标准（实验稿）[M]．北京：北京师范大学出版社，2001：1-8．

[5] 中华人民共和国教育部．全日制义务教育数学课程标准（2011年版）[M]．北京：北京师范大学出版社，2012：1-10．

[6] JONES G A, LANGRALL C W, THORNTON C A, et al. A framework for assessing and nurturing young children’s thinking in probability [J]. Educational Studies in Mathematics, 1997 (32): 101-125.

[7] 许婷婷．高一学生概率认知发展水平的调查研究[D]．苏州：苏州大学，2014：43-54．

[8] 张增杰，刘范，赵淑文，等．5~15岁儿童掌握概率概念的实验研究[J]．心理学报，1982（3）：1-6．

[9] 张增杰，刘中华，邱曼君．5~11岁儿童概率概念认知结构的萌芽及其发展[J]．西南师范学院学报，1983（2）：29-43．

[10] 巩子坤，何声清．7~14岁儿童随机性认知的发展[J]．应用心理学，2016，22（4）：343-351．

[11] 何声清，巩子坤．6~14岁儿童概率概念学习进阶[J]．课程·教材·教法，2017，37（11）：61-67．

[12]  AMIR G S, WILLIAMS J S. Cultural influences on children’s probabilistic thinking [J]. Journal of Mathematical Behavior, 1999, 18 (1): 85-107.

[13]  BATANERO C, GREEN D R, SERRANO L R. Randomness, its meaning and educational implications [J]. International Journal of Mathematical Education in Science and Technology, 1998, 29 (1): 113-123.

[14]  MUNISAMY S, DORAISAMY L. Levels of understanding of probability concept among secondary school pupils [J]. International Journal of Mathematical Education in Science and Technology, 1998, 29 (1): 39-45.

[15]  WASTON J M, KELLY B A. Expectation versus variation: Students’ decision making in a sampling environment [J]. Canadian Journal of Science, Mathematics and Technology Education, 2006 (6): 145-166.

[16]  CHERNOFF E J. Sample space partitions: An investigative lens [J]. Journal of Mathematical Behavior, 2009, 28 (1): 19-29.

[17]  KAHNEMAN D, TVERSKY A. Subjective probability: A judgment of representativeness [J]. Cognitive Psychology, 1972 (3): 430-454.

[18] 何声清，巩子坤．7~9年级学生概率比较的策略及其发展[J]．数学教育学报，2017，26（2）：41-45．

[19] 何声清，巩子坤．7~9年级学生概率认知中的“等可能性偏见”研究[J]．数学通报，2017，56（6）：13-17．

[20] 何声清，巩子坤．11~14岁学生关于可能性比较的认知发展研究[J]．数学教育学报，2013，22（5）：57-61．

[21]  BOROVCNIK M, BENTZ H. Empirical research in understanding probability [M] // KAPADIA R, BOROVCNIK M. Chance encounters: Probability in education. Dordrecht: Kluwer Academic Publishers, 1991: 73-105.

[22]  BATANERO C, NAVARRO P V, GODINO J D. Effect of the implicit combinatorial model on combinatorial reasoning in secondary school pupils [J]. Educational Studies in Mathematics, 1997 (32): 181-199.

[23] 何声清．7~9年级学生对样本空间的理解[J]．中学数学，2017（8）：54-57．

[24] 林群．义务教育数学教科书（九年级上册）[M]．北京：人民教育出版社，2013：132．

[25]  KAFOUSSI S. Can kindergarten children be successfully involved in probabilistic tasks [J]. Statistics Education Research Journal, 2004, 3 (1): 29-39.

[26]  PRATT N C. Is chance fair? One student’s thoughts on probability [J]. Teaching Children Mathematics, 2005, 12 (2): 83-89.

[27]  ZIMMERMANN G M, JONES G A. Probability simulation: What meaning does it have for high school students [J]. Canadian Journal of Science, Mathematics and Technology Education, 2002, 2 (2): 221-236.

[28]  ALBERT J. College students’ conceptions of probability [J]. The American Statistician, 2003 (57): 37-45.

[29]  LIU Y, THOMPSON P. Teachers’ understanding of probability [J]. Cognition and Instruction, 2007, 25 (2): 113-160.

[30]  GARFIELD J, AHLGREN A. Difficulties in learning basic concepts in probability and statistics: Implications for research [J]. Journal for Research in Mathematics Education, 1988, 19 (1): 44-63.

[31] 何声清．叠波模型视角下学生概率比较策略发展的再审视[J]．数学通报，2018，57（8）：7-12．

[32] 何声清．学生概率认知中的典型错误：潜在原因及教学对策[J]．中学数学杂志，2017（8）：15-18．

[33] 何勇刚，张立昌．基于结构方程模型的学习策略影响因素探究——以初中生学习“统计与概率”为例[J]．数学教育学报，2020，29（1）：40-47．

[34] 孙思雨，朱雁．初中生数学自我效能感及其校准性的调查研究[J]．数学教育学报，2019，28（6）：27-32．

[35] 黄翔，童莉，李明振，等．从“四基”“四能”到“三会”——一条培养学生数学核心素养的主线[J]．数学教育学报，2019，28（5）：37-40．

[36] 李红云，朱文芳，伍春兰．学生统计思维发展水平划分探究[J]．数学教育学报，2019，28（5）：41-46．

[37] 邓清，夏小刚．数学思维视域下“教表达”的再认识与思考[J]．数学教育学报，2019，28（5）：47-50．

[38] 凌晓牧，章飞．初中阶段“统计与概率”课程内容的几点建议与调查[J]．数学教育学报，2019，28（4）：77-80．

[39] 朱胜强．数学优秀生教育教学的实践探索[J]．数学教育学报，2019，28（2）：52-55．

[40] 何声清．数学教师KCS与学生认知的一致性研究——以“概率”内容为例[J]．数学教育学报，2019，28（1）：25-29．

The Impact of the Representativeness Heuristic on Middle School Students’ Learning Progressions in Classic Probability

HE Sheng-qing

(Mathematics & Science College, Shanghai Normal University, Shanghai 200234, China)

This study selected 754 seventh to ninth graders as the subjects and explored the impact of the representativeness heuristic on learning progressions in classic probability. It was found that: (1) students’ representativeness heuristic showed a decreasing trend with the increase in grade level; (2) the degree of the representativeness heuristic held by boys was larger than that of girls; (3) there was a significant negative correlation between the representativeness heuristic held by students and their cognition in classical probability; and, (4) students’ representativeness heuristic had a significant negative effect on their learning progression in classic probability, of which the impact of the representativeness heuristic on students’ ability in probability calculation and comparison was especially strong. Three suggestions are put forward for effective elimination of the representativeness heuristic. First, it is unlikely to effectively eliminate the representativeness heuristic by only relying on learning the concept of sample space. Second, only when students have mastered the rules of probability calculation can they effectively eliminate representative inspiration. Third, it is feasible to use extreme examples to help students experience cognitive conflict so as to guide them to discard subjective assumptions when making judgments in probabilistic situations.

representativeness heuristic; classic probability; sample space; learning progressions; mediating effect

G633.6

A

1004–9894（2020）04–0027–07

何声清．“代表性启发”对初中生古典概率内容学习进阶的影响[J]．数学教育学报，2020，29（4）：27-33．

2020–02–25

何声清（1988—），男，安徽安庆人，讲师，博士，主要从事数学教育研究．

[责任编校：张楠、陈隽]