基于数学教学“二重原理”的弧度制教学设计形成研究

常春艳，白慧超，汤志娜

基于数学教学“二重原理”的弧度制教学设计形成研究

常春艳，白慧超，汤志娜

（广州大学 数学与信息科学学院，广东 广州 510006）

从数学史的角度遵循“教与数学对应”原理，明晰数学概念产生的实际问题背景和意义，结合“高中学生数学认知现状”遵循“教与学对应原理”，创设核心问题，构建教学设计路线图，并以个案研究的形式分析教学设计的改进流程，形成体现数学思想方法的教学设计，为数学教师进行教学设计提供可借鉴的参考模式．

弧度制；数学史；数学教学的二重原理

数学教学二重对应原理包括“教与学对应”原理和“教与数学对应”原理[1]．它可以帮助教师将教材中抽象的数学问题变成易于学生掌握的数学知识,形成“教会学生思考”的数学教学设计．但是对于教师如何将原理体现在教学设计并有效应用于课堂教学实践,常常出现“易想难做”的困惑局面．

1 教学设计现状

教师往往依托于教材进行数学教学设计，为此以弧度制为例，从“数学史”的角度切入，分析一下教学设计的“数学史”呈现情况．如表1所示：3个版本的教材从“弧度制”的章节安排上看，都是在“任意角”概念后，但是所呈现的和“弧度制”相关的数学史却明显不同．“北师大版”选择的数学史内容通过“统一单位”讲明了“弧度制”的由来，又用“有利于数学问题的表示和研究”说明了它的用途．“人教版”选择了欧拉的著作更直接点明“弧度制”的数学用途——简化三角公式计算,也就是指向了“弧度制”的应用．这样看来教材试图告诉读者弧度制从“哪里来”，到“哪里去”？“苏教版”并未直接选用“弧度制”的相关数学史内容，但通过“巴比伦”对角度和圆的关系划分，铺垫了“弧度制”的起源．

然而教师们想要将这种思想通过教学设计体现在课堂教学中时，就发生了变化．为此选取百度文库上评分为5.0的10篇“弧度制”相关的教学设计和一篇获奖的说课稿,发现直接选取数学史内容进行教学设计的只有2篇，其中一篇“创设情境，设置疑问”中提到三国时王肃编的《孔子家语》一书中记载有：“布指知寸，布手知尺，舒肘知寻．”[2]一篇依据数学史“弧度制”产生的史料，设计了5个案例，帮助学生理解“弧度制”概念的本质．其它9篇设计中都没有涉及“弧度制”的相关史料和数学思想．

若将这些教学设计进行课堂教学实践，就会出现：将相关史料以故事的形式作为课前导入，或者课中图片展示，又或者课后史料补充，这样既有可能忽视了“数学史”所体现的数学思维方法[3]，也因缺失了学生的互动，错过了“教学生成”的教育智慧，最终都有可能将偏离“教会学生思考”的最终目标．因此，掌握体现“数学”的教学理论基础就尤为必要了．

表1 不同版本《弧度制》中数学史内容比较

2 理论基础

数学教育具有一般教育过程的性质[4]，又具有自身特殊过程的性质，这种双重性质的数学教育过程构成了数学研究的对象．建立于这样的思想基础，数学教学问题的研究就得以沿着“教与学对应的原理”和“教与数学对应的原理”的理论基础进行设计，这样才能更好地帮助学生理解“弧度制”概念本质，才有可能更好地应用弧度制解决数学问题和实际生活问题．

2.1 教与学对应

“教与学对应”的原理指出[5]，数学教学需要根据学生的“学”来确定教师的“教”，即根据学生的基本学情和课堂的应然表现，来确定教学的目标、内容、方法和流程等．这样看来尽管“弧度制”概念是统一的，但是基于不同学生的理解，就需要设计出符合学生认知规律的教授内容．而了解他们的认知难点是最直接获取学生数学认知规律的方法．其实对于大多数学生而言，弧度和角度的换算并不是理解上的难点．事实上，很多高中学生对于弧度制的概念和弧度角的概念比较难以辨析．这是因为在日常生活中，他们已经熟练掌握了用角度制来衡量角的大小，熟悉了角度制的应用．所以根据这个认知现状，要从学生的生活情境出发，完成从已知的角度制到未知的弧度制的认知同化．

2.2 教与数学对应

数学教学不是仅仅研究“教学”，更要研究教育中的数学，要把教育与数学的本质对应起来．就数学的本质而言，它和形式是事物存在的两个方面．本质是事物本身所固有的根本属性，形式是事物内容的组织结构和表现方式．对于一个数学对象（概念、法则、公式、定理等），它的形式可能是多样的、可变的，它的本质却始终是恒定的、不变的．这就是说，数学的学习，不仅要学习它的形式（记住符号），更重要的是把握它的本质（理解其在特定范围内始终不变的特质）．就“弧度制”的本质理解而言，从数学史的发展，更容易体会到它不同于教材中静态的定义表述，它是一个动态的发展过程，伴随数学学科的发展，它的本质逐渐显露．

首先，它具有“问题”本质[6]．它起源于实际的天文学问题，应用于广泛的几何问题．而且伴随科技的发展，这一概念将会表现出更丰富的内涵．所以围绕“问题”展开教学设计，让学生理解“弧度制”问题的缘起、发展和应用，既有利于学生对弧度制本质的把握，又可以起到建构新知识的导航作用．

其次，它以“比值”的形式将角数值化，从非连续的自然数集转化成了具有连续性的实数集．可见，同一数学对象的不同表达形式正是变更非本质特征的表现方式，从不同侧面突出了数学对象的本质特征．如果在概念学习中，注意从不同角度对对象的不同表现形式进行一系列的加工处理，形成以相关属性为纽带的网络结构，那么，在不同的情景中就可以根据问题的形式和内容，提取出相应的有针对性的处理策略，就易于真正把握数学对象的本质．所以“比”是其根本属性，而“比”的本质，又要求两个数量关系单位一致，这就为“角度制”向“弧度制”的转化提供了自然过渡．

基于以上分析，制定以下教学设计框架．

3 教学设计框架建构

3.1 围绕二重原理预设教学设计

由“教与学对应”和“教与数学对应”的二重原理进行弧度制的教学设计[7]，要遵从学生的认知现状和数学问题本质进行内容整合．

（1）基于学生认知创设教学情境，体现“教与学对应”．

首先，学生已有的数学知识和认知经历如表2．

从表2中可以看到学生已有：图形中角的概念和π的初步认识，0°~360°角的认知和画法，以及π和圆的关系．同时，在学习上述内容的过程中，学生已有角的相关认知经历：从静态角的定义到动态学习经历；部分学生了解无理数“π”和“角”的关系；初中的锐角的正弦、余弦和正切计算方法等．这些都直接有利于“弧度制”概念同化．

表2 与“弧度制”相关的教学内容

其次，为了学习未知的“弧度制”这个新概念，要明确采用哪一种概念教学模式更为适合？这就需要根据学生的认知结构现状选择适合的“概念同化”和“概念形成”模式进行教学设计（如表3）．

表3 “弧度制”概念的教学模式

根据预设内容，就可以围绕这一概念教学模式进行相应的教学设计内容安排，比如概念同化要创设的情境，是便于利用先前的认知结构从角的认识上进行上位学习，明确“角度制”和“弧度制”是同一个事物的两个不同表达形式．而概念形成则要围绕实际生活中“角”的应用实例去感悟“弧度制”存在的必然性与合理性．

（2）基于数学史料设计核心问题，体现“教与数学对应”．

教学设计中的情境不仅要考虑学生的接受程度，更要尊重数学史实，尽可能地揭示数学问题本质，即要满足“教与数学对应”原理．它主要指教学的内容与数学知识对应，教学的知识结构与数学知识结构对应，教学情境与数学对象的本质对应，教学的思维方法与数学思维方法对应教学中的研究方法与数学研究方法对应，教学中的表达方式与数学表达方式对应．在教学中把握核心概念和教数学的“大方法”．

因此，以“弧度制”概念教学而言，要明确它“比”的本质，要熟悉把握“角”的度量中，不同单位制下的表达形式和表达形式之间的联系，进而解决“弧度制”的核心问题．这就需要根据数学史进行情境创设揭示“角”的变化特征，既有利于学生在情境中获取“角”直观表象，又与实际问题相联系．为此，首先通过数学史的文献的阅读[8]，挖掘相关弧度制中蕴含的数学知识和数学问题，然后根据教学目标，梳理出弧度制的核心问题，如表4所示．

3.2 围绕核心问题形成教学设计框架

确立“为什么”和“有什么用”是“弧度制”课堂教学的核心问题后，教师需要结合教学现状，利用教材创设情境，使这两个问题成为课堂教学的“驱动力”，既要它驱动学生朝着解决这两个问题的方向不断深入思考，逐步揭示弧度制的概念本质，又要它引领教师通过解决这些问题，教会学生学习更一般数学概念的科学研究方法．

（1）直线型教学设计．

表4 “弧度制”教学设计预设核心问题

围绕人教版的教材内容，采用概念形成的形式进行问题情境设计，根据数学史所体现的科学和数学价值[9]，以及便于学生更好联系实际的生活价值，形成如下教学设计的框架，这就需要根据这个标准选择弧度制的例子（如表5）．

表5 弧度制的“直线型”教学设计框架

（2）循环型教学设计．

灵活地将教学内容以循环的方式体现出来，从数学史的材料中选取一些角度制无法解决的问题，将其用“数学化”的方法，通过计算，发现新的度量角的方法——弧度制．再通过合适的数学模型思想，建立“弧度制”的应用，与角度制的应用呼应，做到从“产生问题出发，回到解决问题”，有助于学生形成解决一般问题的科学研究方法中来．这种设计可以看作是一种“概念同化”的教学方式，需要学生对角有一定的认知结构和相应的运算技能，便于在解决问题的过程中，更好地理解“弧度制”的“比值”本质（如图1）．

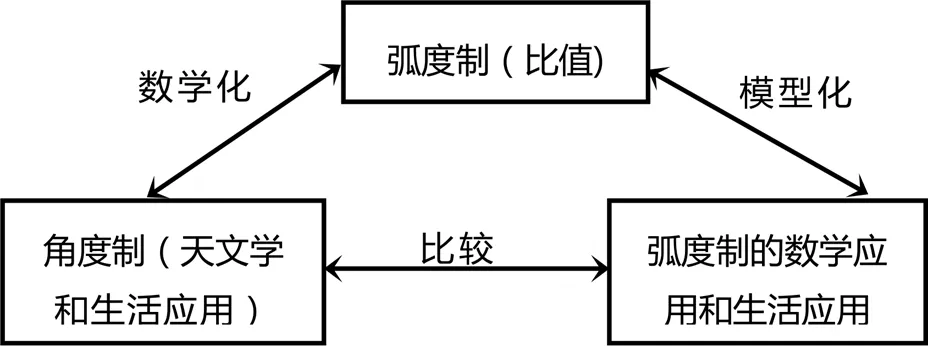
图1 弧度制的“循环性”教学设计框架

4 教学设计的实践

根据预设的教学设计框架，依托某校高二学生的认知基础，教师A选取数学史的相关内容，完成“弧度制”的教学设计，并针对“核心问题”不断修订，进而通过课堂教学实践检验逐步完善．

4.1 教师的教学设计初稿

教师A围绕“弧度制从哪里来？”和“弧度制有什么用？”教学设计初稿配图如图2．两个核心问题梳理对相关的数学史实进行梳理，在课堂教学中形成了如下教学片段．

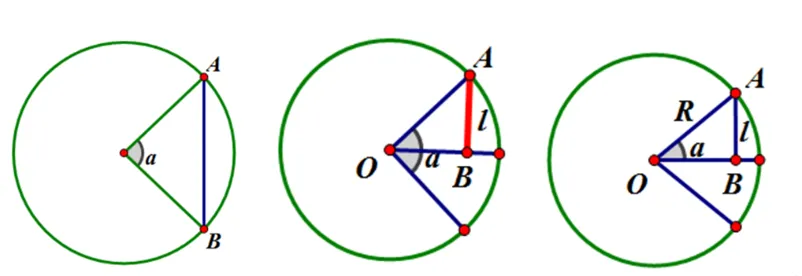
图2 弧度制教学设计初稿配图内容

【片段1】以“古希腊对正弦定义”形成认知冲突，引发学生兴趣．

【片段2】“托勒密的部分弦表”[10]，让学生直观看到“度可以是弧长的单位”

【片段3】数学家阿耶波多弧长与弦长均采用60进制，但是他们的单位却是不同的．圆周长是分为360份，以1/360为单位，而弦长是在将半径分为60等份，取半径的1/60作为长度单位．

做出如上的设计是因为教师主要考虑到下述教学问题．

（1）如何理解弧度制的概念？可以从“了解弧度制出现的原因”开始学习，如片段1、2、3．

（2）如何能对弧度制的适用性有更加深刻认识？参见片段4和5．

（3）如何从心理上更自然地接受弧度制？

从图2中进一步分析可以看出，弧度制概念形成过程的合理性：从圆心角所对的弦和弧考虑，到圆心角所对半弦，再到圆心角的一半所对弦的猜想，清晰的表明了人类对“角”大小衡量方法的思维变化．但是以下问题值得深入分析．

Q：弧度制的本质是什么？

A：用“边”的关系描述角．

Q：边的什么关系呢？

A：比值．

Q：弧度与角度的异同？

A：都是描述角的大小，单位制不同！

Q：弧度制的产生过程的数学思想是什么？

A：统一单位，化曲为直．

结合这样的分析，教师A对图2所采用的配图提出质疑，担心学生认知水平不够，难以理解，于是依据“教与学对应”和“教与数学对应”的双重原理基础，回到“弧度制”概念本质，修改教学设计．

4.2 教师的教学设计修改版

考虑弧度制的本质是一个比值，采取概念同化的方式，借鉴数学史资料提供图3所示的配图，便于学生发现“弧度制”概念缘起．

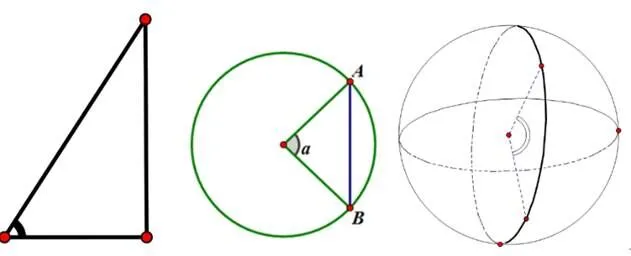
图3 弧度制教学设计修改稿配图内容

【片段6】请学生说出角在哪里？根据配图，可知在学过的直角三角形、圆、球中，是从简单的图形中认识角．但古人却是从复杂的图形中认识角的，这就是托勒密研究天文学中发现和应用的角．

【片段7】无论在哪个图形中，都要明确一个目的角的用途什么？度量！度量所在图形中的各个线段的长度，面积大小等．那么在三角形中的角，可以通过量角器，锐角的正弦公式计算而得，在圆和球中呢？为了研究问题的方便，仅研究这个圆中的角还有什么别的方法能进行度量？

【片段8】启发探究，在图3中，怎么进行度量角的大小呢？没有直角三角形，就构造直角三角形，所以出现了弦长的关系，顺其自然介绍数学史上各位大家的方法．

教师A利用概念形成的教学模式，借鉴正弦的“比”的概念，推导出弧度的比，若能启发学生说出，角的大小是通过“曲线与直线”的比转化成“直线比直线”的关系而加以界定，“弧度制”的概念本质将更加清晰．

4.3 课堂的教学设计实践

为了更好的突出“弧度制”的概念本质，教师A再次明确弧度制的教学目标为下述3个：（1）体会“度”也可以用来表示“弧长”；（2）理解弧度制出现的来由，理解角的概念；（3）体会弧度制在高中学习中的实际应用．为此确立了新的教学思路为：弧长用“度”来衡量—弦长由“半径”求出—弦长与半径单位不同（量直线与曲线单位不同）—统一弧长与半径单位—托勒密的方法—阿耶波多的方法—欧拉方法—弧度角的定义—总结弧度制的意义，并最终选择了以下教学配图，通过课堂教学实践进一步完善，形成下述教学片段．

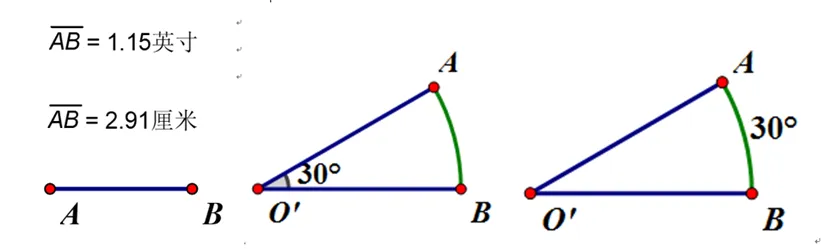
图4 弧度制教学设计课堂实录稿配图

【片段9】试用不同单位制度量同一线段AB的长度，启发学生进行类比思考尝试认识同一角度的不同表述．

【片段10】同学们先看下图，老师画出了一个角，角度为30°，我现在请一位同学来给我标记一下．

【片段11】师：现在对于一弧度角的描述，你明白了吗？结合图5，我们可以计算出1弧度角和角度角的关系，所以1 rad角比1°大很多呢！

另外弧度制还可以应用于简化物理学中圆周运动相关公式，以及高等数学部分极限公式和微分公式。这些都是弧度制为我们提供的便利应用，它不仅简化了公式便于计算，更为科学合理地描述事物本质提供了思维方法．

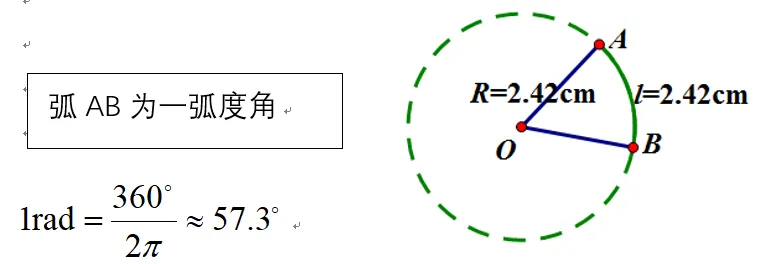
图5 一弧度角

通过观摩课后教师评价反馈，这样的教学设计创新度高，体现数学思想方法及数学问题的应用，是一次很好的尝试．但是鉴于学生的认知程度不同，有些细节还需要不断完善．比如考虑正弦函数自变量时，只能选用“弧度制”表示角的范围，这是由函数定义决定的．但学生们往往会忽视“两个非空数集”的本质属性，错用“角度”表示，实际上严格的“1°”表示的一个图形，而非“数”．

5 启示

通过课堂教学实践，教师们不仅发现数学史应用于教学设计对学生数学能力的提升空间很大，比如“托雷密弦表”中的（0.5°）的弧长对应着0°31′21″是怎么算来的？这样细节的问题，若师生合力探究，不仅加深“弧度制”的理解，而且解决这个问题的过程中用到了“托雷密定理、托勒密弦表、60进制与10进制的转换、圆内接正多边形的做法”等知识，充分实践了“发现问题，解决问题”的有效策略．其次将数学教与学“二重原理”贯穿于数学教学设计，绝非一件易事，它不仅需要精通数学，更要依据学生的认知现状将教室外的天文、大自然与日常生活等现象，经过长期的观察和体验，形成教室内的数学问题，然后围绕数学问题的本质，数学问题所蕴含的思想方法，通过数学教学原理的设计应用，让学生更好的理解数学概念，更有效的解决实际问题．

[1] 涂荣豹．“教与数学对应”原理的实践——对“函数单调性”教学设计的思考[J]．数学教育学报，2004，13（4）：5–9．

[2] 风雨56910．弧度制教学设计[EB/OL]．（2018–06–29）[2018–10–21]．https://wenku.baidu.com/view/095674cd9ec3d5bbfd 0a745a.html?from=search．

[3] 汪晓勤，张小明．HPM研究的内容和方法[J]．数学教育学报，2006，15（1）：16–18．

[4] 涂荣豹．试论数学教育研究的规范性[J]．数学教育学报，2003，12（4）：1–5．

[5] 中央教育科学研究所．陶行知教育文选[M]．北京：教育科学出版社，1981：77．

[6] 沈威，曹广福．高中三角函数教育形态的重构[J]．数学教育学报，2017，26（6）：14–21．

[7] 郑庆全，涂荣豹．数学教育研究的“双向建构”和“二重原理”思想的实践[J]．数学教育学报，2008，17（6）：33–36．

[8] 徐章韬．基于数学史的弧度制概念的教学设计[J]．湖南教育，2008，12（1）：41–42．

[9] EVES HOWARD. Great moments in mathematics (Before 1650) [M]. The Mathematical Association of America, 1980: 1.

[10] 蔡聪明．星空灿烂的数学——托勒密如何编制弦表[J]．数学传播，1999（90）：57–67．

Design-Based Research on Instruction of the Topic of Radian Measure with Respect to the Dual Principle of Mathematics Education

CHANG Chun-yan, BAI Hui-chao, TANG Zhi-na

(Department of Mathematics and Information Science in Guangzhou University, Guangdong Guangzhou 510006, China)

This study presented the background and significance of the historical development of the topic of radian measure. In consideration of “teaching corresponding to learning” and “high school students’ mathematical cognition”, we attempted to create key instructional tasks and established a map for instructional design. We then analyzed and modified a teaching case so as to provide a detailed process model for teaching, which reflects historical development of the topic.

radian; history of mathematics; dual principle of mathematics education

2020–02–06

2018年度广东省高等教育改革项目——基于新师范建设的数学教学技能训练模式和路径研究（粤教高函【2018】180号–458）

常春艳（1977—），女，山西太原人，博士，副教授，主要从事数学课程与教学论及数学教育心理学研究．

G421

A

1004–9894（2020）04–0034–04

常春艳，白慧超，汤志娜．基于数学教学“二重原理”的弧度制教学设计形成研究[J]．数学教育学报，2020，29（4）：34-37．

[责任编校：陈汉君、陈隽]