数学试卷综合难度的内涵及其指标体系建构

吕世虎，于丽芳，王尚志

数学试卷综合难度的内涵及其指标体系建构

吕世虎1，于丽芳1，王尚志2

（1．西北师范大学教育学院，甘肃 兰州 730070；2．首都师范大学，北京 100048）

数学试卷的难易取决于客观和主观两方面：客观方面指作为客体的试卷本身内容和结构所决定的难易，即绝对难度；主观方面指作为实践主体的学生其水平所决定的难易，即相对难度．数学试卷的难度是主观与客观的统一，由绝对难度与相对难度共同决定．基于此，提出数学试卷综合难度的概念，并结合已有文献选择部分中考数学试卷为案例进行量化分析，构建用试卷题型及其顺序、试卷题量与考试时间、试题难度分布、试卷阅读量、试卷新颖性、学生实际水平等6个要素刻画的数学试卷综合难度指标体系．

数学试卷；综合难度；指标体系

1 问题提出

2018年8月教育部启动中考命题评估工作，目的之一是“构建命题质量保障和提升机制”，促进命题单位改进命题工作．命题评估包括对试卷质量的评估，一项重要的指标是试卷难度．在对各命题单位提供的数学试卷信息进行分析时，一贯用得分率评判数学试卷难度的方法出现了问题，不能清晰地给出判断，疑问之处颇多，以下举其中两种情况为例予以说明．

第一种情况的问题出现在对E、F两个地区试卷难度评判过程中．E、F两个地区试卷相关信息如表1~表3所示．

表1 E和F两地区试卷信息a

根据表1的数据，按照得分率来判断两地区的试卷难度，得分率高的试卷容易，得分率低的试卷较难．E地区试卷得分率为0.73，F地区试卷得分率为0.49，因此F地区试卷难度大于E地区．但是，若将两地区试卷题量（试卷中的小题数）纳入考虑（如表2所示），便出现疑问．

表2 E和F两地区试卷信息b

根据表2的数据，E地区试卷题量为40，F地区试卷题量为29，也就是说E地区学生需要完成的试题数量比F地区学生多11．尽管从得分率来看E地区试卷难度小于F地区，但E地区试卷题量远大于F地区，据此能否判断为两地区试卷难度相当呢？

进一步把考试时间纳入进行分析（如表3所示），也会出现疑问．

表3 E和F两地区试卷信息c

根据表3中的数据，E地区考试时间为120分钟，F地区考试时间为100分钟．E地区考试时间长，学生答卷时思考的时间多，但由于题量大，所以试卷难度不小；F地区考试时间短，学生答卷思考时间少，但由于题量少，所以试卷难度也不是很大．能否就此解释为E地区和F地区的数学试卷难度相当呢？

第二种情况的问题出现在对M、N两个地区试卷难度评判过程中．M、N两个地区试卷信息如表4、表5所示．

表4 M和N两地区试卷信息a

根据表4中的数据，M和N地区试卷的题量、考试时间相当，题量分别为36、32，考试时间均为120分钟．两份试卷的得分率分别是0.64、0.62，可以判断M地区和N地区数学试卷难度相当，这似乎没有疑问．

表5 M和N两地区试卷信息b

然而根据表5中的数据，两份数学试卷字符数（即试卷阅读量）M地区为3 693，N地区为1 605，M地区数学试卷的阅读量明显大于N地区．按照第一种情况的分析思路，虽然两份试卷得分率近似，但M地区学生在相同时间内需要阅读、理解、甄别大量信息，N地区学生需要阅读、理解、甄别的信息相对少了许多，能否解释为M地区试卷难度大于N地区呢？

从上述两种情况中可以发现，根据不同的试卷信息判断试卷难度会出现不同结果，依据得分率判定数学试卷难度的合理性值得反思．目前对试卷难度并没有明确界定，许多教育测量学专著和考试理论研究文献将难度视为试题分析的一个参数，对数学试卷难度的研究大都聚焦于试卷中试题的难度，主要围绕内容难度与统计难度进行．内容难度是依据试题所属知识水平层次、试题所考查知识点的深广度、推理步骤及技巧的灵活性等所作的难易程度的判定．统计难度则是考试后用统计的方法计算得到的难度值，即得分率．一道试题的难度就是考生对该题的通过率或得分率．对于答对得1分，答错或不答得0分的试题，难度就是答对试题的人数与考生总数之比．对于满分大于1分的试题，难度则是考生对该题的平均得分与该题满分量之比．不难发现，将试卷难度主要指向数学试卷中的试题难度，对试卷的难度衡量并不是很全面，试题难度与试卷难度毕竟不能等同；而得分率只考虑学生的成绩，并未将影响试卷难度的其它方面纳入考虑．

至此可以肯定得分率已不足以刻画数学试卷的难度，数学试卷难度不只是统计难度（得分率）、内容难度，还包括试卷结构（如试题数量、考试时间、试卷阅读量等）带来的难度．那么，数学试卷难度的内涵是什么？影响数学试卷难度的要素有哪些？这是研究探讨的主要问题．

2 数学试卷综合难度的内涵

难度是客体妨碍主体认识和实践的阻力程度[1]．数学试卷作为考查学生能力水平的工具，其对学生完成答卷的阻碍是多方面的．作为妨碍学生完成答卷的客体，其阻力程度一方面来自于客体自身客观存在的阻力，即试卷内容、结构带来的阻力；另一方面来自于主体自身能力水平的大小，学生作为完成答卷的实践主体，其自身的思维、能力水平各不相同，面对试卷客观存在的阻力其表现度（或感受度）也是不同的．如果说试卷内容、结构带来的阻力是数学试卷这一客体的绝对难度，那么，当面对着具体的主体时绝对难度发生变化，即学生的实际水平使得试卷的绝对难度具有了相对性．

研究者从主客体统一的角度出发，综合试卷内容、结构、学生能力水平提出数学试卷综合难度的概念：数学试卷综合难度是指数学试卷的内容、结构妨碍学生完成答卷的阻力程度．数学试卷综合难度是数学试卷作为客体对实践主体学生的阻力程度，包含主体和客体两个标向，是主客体的统一，对数学试卷难度的刻画是整体性的．以往对数学试卷难度的判断大多利用试题内容难度或得分率，而试题内容难度只是试卷绝对难度的一部分，得分率则是在试卷投入使用测试结束后，着重反映试题内容难度的指标．以此评判试卷难度对命题者改进命题、提升命题质量提供的信息不全面，对数学试卷难度的评判也缺乏整体性．尽管对学生主要的阻力来自试题的内容难度，但展现在学生面前的是一份完整的试卷，其结构因素仍会为学生完成答卷带来相应的阻力，且其阻力程度是不能忽略的．已有研究也涉及到部分试卷结构因素，但这类研究并没有将试卷结构与试卷的难度紧密联系起来，只是就命题过程中试卷结构的技术指标而言的[2]．

3 数学试卷综合难度指标体系

数学试卷综合难度从主客体统一的角度，整体阐述了数学试卷中的绝对难度与相对难度．绝对难度即客体自身存在的难度，包括试卷内容和结构两部分，相对难度由实践主体学生的实际水平决定．因此，数学试卷综合难度指标体系包括以下6个方面：试卷题型及其顺序、试卷题量与考试时间、试题难度分布、试卷阅读量、试卷新颖性、学生实际水平．前面5个指标体现在数学试卷内容和结构方面，学生实际水平体现在绝对难度的相对性．

在数学试卷内容和结构中，不同题型对学生运算量、思维量以及数学表达的要求程度不同，题型的选择及其顺序安排影响试卷的综合难度．题量的多少以及考试时间的长短对学生用于解答每道题的时间有客观限制，会引起试卷综合难度的变化．不同难易水平的试题需要学生理解、掌握的知识量不同，思维层次也不一样，反映试卷中易中难试题多少的试题难度分布就成为影响试卷综合难度的一个要素．试卷阅读量的大小因与题型、时间关系密切，不仅考查学生的理解能力，而且考查学生的阅读能力及解题速度，同样影响试卷的综合难度．试题的新颖性反映了试题对学生的挑战度，也影响试卷的综合难度．学生实际水平则是影响试卷综合难度的关键指标，不同地区学生生活经历、知识水平、思维发展的差异决定了学生完成答卷阻力程度的不同．

以上数学试卷综合难度的指标是否合理呢？研究者选择2018年东部、中部、西部省（市）中考数学试卷共32份进行分析，通过对这些试卷的定量与定性分析阐释数学试卷综合难度6个指标的合理性．由于所选取的试卷中并非每一份试卷各方面数据都完备，因此每一指标可能选取不同试卷数据进行定量分析．

3.1 试卷题型及其顺序

数学试题按题型可分为是非题、选择题、填空题和解答题．是非题即判断对错题，指判断基本概念、关系、命题的真假的试题．选择题包括单项选择题和多项选择题[3]．填空题是对某些基础知识、简单计算问题等的要素或结果设置空白，让学生填出正确结果的试题．解答题包括求解题、证明题、应用题、开放题和探究题等，是要求学生写出求解、证明、分析或探索过程的试题[4]．有研究也将数学试题类型分为主观题和客观题，其中解答题属于主观题，其余属于客观题；也有研究将题型分为选择题和非选择题[5]．中国中考数学试卷中的题型有选择题（特指单项选择题）、填空题和解答题3种．选择题的正确答案唯一，答案的范围明确，学生只需进行选择，难度较低；非选择题具有一定的开放性，没有提示可能的解题思路，而且能够较为全面地考查学生的能力，相对选择题来说难度较大．填空题不需要写出思维过程，不考查学生的数学表达，但没有答案选项提示，所以其难度相对选择题来说稍大，相对解答题来说较小．从这个意义上说，一份数学试卷中选择题难度最低，填空题难度次之，解答题难度最大．

题型顺序是指在一份数学试卷中不同类型试题呈现的次序，题型呈现的顺序也会引起试卷难度的变化．在收集到的数学试卷中，云南省中考数学试卷的题型顺序不同于其它试卷，先呈现了填空题，其次是选择题和解答题．在对云南省中考数学试卷进行分析后发现，试卷中试题内容难度一般，都是比较基础的题目，甚至是相对容易的，其中也没有新颖的、探究性的或是背景复杂的试题，但考试后的得分率很低．因此可以推断，其中一个原因可能是试卷题型的顺序安排带来了试卷难度的增加．上述题型难度是从一般意义上来说的．实际上，题型难度具有相对性，有些选择题可能会比填空题甚至解答题都难．中国中考数学试卷的题型设置一般情况为选择题、填空题、解答题，试卷中的顺序也是如此．

不同难度题型及其呈现顺序会影响试卷的整体难度．命题时在选择题、填空题、解答题3种题型中选择一种、两种或3种题型及每种题型呈现的顺序，对学生完成答卷的阻力程度是不同的，对试卷综合难度也是有影响的．在试卷难度评估时，不能忽略试卷中题型及其顺序这一要素；在命题、组卷时，可根据具体的难度要求，通过调整试卷题型及其顺序调整试卷的综合难度．

3.2 试卷题量与考试时间

试卷题量也称作试卷长度，在一份数学试卷中试卷题量常指小题数量，即若一道解答题分3个小问，则按照3道题计算．题量与考试时间共同决定了学生解答一道试题所用时间的长短．每一道试题都需要学生花费时间进行理解与分析，对试题不同程度的理解与分析反映着试卷阻碍学生解答的不同阻力程度．相同考试时间内，题量大的试卷学生平均解题时间少，且试卷考查的知识点较多，学生进行的运算量、思维量大，而较短时间的思考引起理解与分析得不透彻，试卷难度会增加；相反，题量少的试卷学生平均解题时间充足，可以对题目进行清晰、完整、透彻地理解、分析与解答，试卷的难度会相应减弱．很多学生在考试时对于费时多、得分少的试题选择放弃，原因也在于此．因为这样的试题耗时长，无形之中“缩短了”对其它试题的思考与解答时间．因此，命题时试卷中甚至试卷每一题型中的题量都需要仔细斟酌，考试时间的长短也应与题量相协调[3]．

中国中考数学考试时间多为120分钟，极少地区为100分钟，通过统计32份数学试卷中题量与考试时间的设置发现其差异较大，试卷题量在29~42之间，考试时间与试卷题量之比在2.86~4.00之间，题量差距过大，试卷题量与考试时间之比也差距悬殊．以福建省与海南省、广西柳州市与甘肃平凉市的中考数学试卷为例，题量与考试时间信息见表6、表7．

表6 福建省与海南省中考数学试卷题量与考试时间

从表6可以看出，福建与海南两个省份同属东部地区，福建省考试时间为120分钟，题量为30，海南省考试时间为100分钟，题量为29，在题量差距不大的情况下，考试时间相差20分钟．在考场上多出20分钟的时间，意味着学生的思考时间大不同，足以引起两个省份的试卷难度差异，可以推断：福建省试卷得分率高而海南省试卷得分率低．两地2018年中考数学的学生测试成绩，福建省得分率为0.59，海南省得分率为0.49，与上述推断一致．

表7 广西柳州与甘肃平凉中考数学试卷题量与考试时间

从表7可以看出，柳州与平凉两个地区同属西部，考试时间均为120分钟，试题总题量分别为32和38，差距较大，同样长的考试时间，平凉市的学生要多做6道题，尽管6道题可能是很简单的试题，但也需要一定的时间理解题意、分析问题，之后再进行解答．6道题目的思维量与运算量对试卷整体难度的影响是显而易见的．可以推断：柳州市试卷难度小而平凉市试卷难度大．两地2018年中考数学的学生测试成绩，柳州市得分率为0.62，平凉市得分率为0.54，实际数据与上述推断一致．

关于题量引起的难度变化也存在于每一种题型中．在所选32份中考数学试卷中，选择题数量在6~16之间，填空题数量在3~12之间，而解答题小题数量在11~26之间，每一种题型中最多题量与最少题量差距更加悬殊，加之题型自身存在难度差异，不同题型的题量不同使得各地数学试卷难度差异很大．以河北省与江苏省中考数学试卷为例说明，试卷信息见表8．

表8 河北省与江苏省中考数学试卷题量与时间信息

两个省份同属东部地区，考试时间均为120分钟，试题总题量、解答题量相差不大，在选择题与填空题中的题量差距很大．选择题对学生解答试卷的阻力程度相对较小，而填空题相对选择题的阻力程度要大．选择题河北省设置16道，而江苏省只有6道；填空题河北省设置3道，而江苏省设置10道．两份试卷在题型中的题量差异带来了试卷综合难度的差异．

一次考试中考试时间有限，如何适当控制题量，帮助学生把有限的时间配置到适合自身难度的题目上去，争取最大化地展现学生的才能是命题面临的难点[7]，也是命题人员在把握试卷难度时必须考虑的重要方面，在试卷难度评估时也不得不加以考虑．

3.3 试题难度分布

刻画数学试卷的综合难度，离不开试题的难度（即试题的内容难度）及其分布，试题内容难度的确定要结合具体的知识点及思维量来判断，考查不同知识点的试题其运算量、思维量等也不尽相同[7]，不同的知识点对于不同水平的学生难度也不同，但不同难度水平的试题分布可以调整，并藉此调整试卷综合难度以适应学生的实际水平．

数学试卷中试题难度分布是指试卷中不同内容难度试题在各难度水平的分布情况，即命题人员设置的试卷中各级难度试题的比例，也就是通常意义下的各级难度试题的分值比例．在数学试卷中试题难度分为易、中、难3个层次，相应难度的题目也称为基础题、提高题、见解题．通常情况下，难度在0.7以上的试题为容易题，难度为0.4~0.7的试题是中等题，难度在0.4以下的试题为难题，试卷由3种难度的试题组成．中国中考数学试题难度比例的设置目前没有明确规定，根据中考数学考试评价的目的，有几种试题难度分布类型，易中难的比例分别是6∶3∶1或7∶2∶1或8∶1∶1，有研究对这3种比较常用的试题难度分布运用数理统计的方法进行了研究，肯定了其合理性[8]．

已收集到的32份中考数学试卷的难度分布中，各地的数学试卷试题难度分布大都集中在7∶2∶1和6∶3∶1两种，不同试题难度比例之下，呈现出的试卷难度也不同．题量固定时，容易题型设置过多则对中等学生和能力较强的学生不易鉴别，中等难度题设置过多则没有照顾到薄弱学生的水平，对能力较强的学生也不能很好地鉴别；难题设置过多则中等和薄弱学生的水平不易鉴别．中考试卷中有的试卷简单题目设置较多，而有的试卷较难的题目又设置得过多，易中难试题比例不协调，由于试题难度分布而引起的试卷难度变化是实际存在的．以上海市和山西省为例，上海市命题组对试卷的难度比例设置为8∶1∶1，山西省试卷难度比例设置为6∶2∶2，很明显，上海市试卷容易题设置过多，中等难度题较少；山西省试卷容易题设置较少．从试题难度比例上反映出，上海市试卷对学生解答试题的阻力较小，而山西省试卷对学生解答试题的阻力较大，这样的试题难度分布体现出试卷对学生完成答卷的阻力不同，因而影响试卷的综合难度．

3.4 试卷阅读量

在一份数学试卷中，试卷的阅读量可以用整份试卷中文字及符号字符数的多少来刻画，字符数包括试卷中出现的所有的中文、英文、数学符号等，不包括图形和标点符号．试卷阅读量的大小取决于试卷中每道试题阅读量的大小．在一些试卷中对部分试题的描述或背景介绍使用了大量的笔墨，以文字语言为主，辅以符号语言．学生解答时必须读懂题，充分理解试题中的数学术语及关系以及文字、图形、符号的含义等，完成文字语言与符号语言的互译，才能运算求解[9-10]．这些字符增加了题目语义信息的复杂性，需要学生对语意信息非常敏感，对信息区分策略使用非常灵活，增加了问题表征的难度，因此也增加了试卷的难度[11]．

统计了32份中考数学试卷的字符数及平均阅读量，见表9．中考数学试卷的字符数在1 605~3 693之间，平均2 515个字符，考试时间多为120分钟，平均阅读量约为每分钟21个字符．字符数最少的试卷每分钟13个字符，字符数最大的试卷每分钟31个字符．

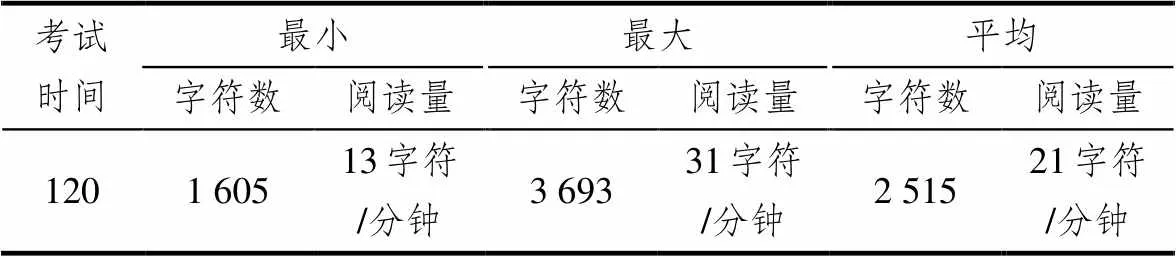
表9 中考数学试卷字符数

中考数学试卷中字符数相差巨大，最大字符数试卷与最小字符数试卷的字符数相差2 088，相差的字符数比最小字符数试卷的字符数还多，而最大字符数试卷的阅读量是最小字符数试卷的阅读量的两倍多，以2018年宁夏中考数学试卷为例，试卷字符数为3 228，其中解答题第25题字符数多达1 048，且不包括题目中附的图形，仅一道题在试卷中所占版面接近A3纸张一面，字符数占试卷总字符数约三分之一．这样的试题设置（问题表征）语意冗长，关系更加复杂，对其阅读、理解都需要较好的记忆力和清晰的思路，还要同时进行分析与作答，学生解答时所用时间格外多，难度过大．

对于学生来说，熟悉数学语言（包括文字语言、符号语言、图形语言）是阅读、理解和表述数学问题的基础[12]．在解答有一定阅读量的试题时，学生首先要进行字面的理解，然后对其进行概括、抽象，接着对其做出个人判断并进行解答．阅读量大的试卷对学生的数学阅读、抽象、概括等能力提出了更高的要求，在学生进行理解、分析与解答的每一个环节都设置了障碍．学生如果对题意都无法理解，那么便谈不上分析问题、解答题目了；在理解了题意的前提下，如果学生的概括、抽象等能力较弱，仍然不能对题目做出正确解答．可以说，试卷的阅读量对试题的解答设置了层层障碍，重重阻力，影响着试卷的综合难度．在试卷命制过程中，可通过设置有一定阅读量的题目来调控试卷的综合难度，对试卷难度的评估也应同时考虑这一要素．

3.5 试卷新颖性

数学试卷的新颖性是数学试卷中试题新颖性的整体体现．新颖的数学试题在引导学生构建知识网络、掌握数学思想方法的同时，有利于发展学生的数学阅读能力、分析问题和解决问题的能力，有利于培养学生的数学兴趣和爱好，也有利于学生创新能力的培养和创新意识的提高[13]．试题的新颖性主要体现在试题情境、设问方式、解决思路等方面[14]．

新颖的试题情境打破了学生日常解题的思维定势或思维习惯，解决这类问题需要有新的思路或方法．新颖的设问方式主要有开放式设问、探究式设问、实践式设问等，试题答案不一定唯一，主要对学生的数学理解及思维的灵活性进行考查[15]．学生初次接触这样的题目时，在信息提取方面有一定难度，如果学生已有数学知识基础不够扎实，缺乏其它学科中的必要知识，或者对实际生活中的数学知识无法进行抽象概括，能否理解题目的意思或许会成为首要问题，要解决问题则难度更大．试卷中试题独特的设问方式则要求学生以相对陌生的思路对试题进行理解、分析与解答，常常会引出不同于平常的解题思路和方法．试题文字语言的呈现、图表语言及数学语言的创新表达等不仅考查学生提取信息、分析信息的能力，还要求学生对信息进行加工，同样使得试题难度加大．另外，新颖的数学试卷往往对数学思想方法的运用要求较高，而数学思想方法是数学知识在更高层次上的抽象、概括与提炼，学生一则要熟悉这些思想方法，二则要根据试题情况进行方法的具体选择，这是一种高水平思维的考查，对学生具有较高的难度，形成的试卷也相对较难[6]．

新颖的试题情境和独具特色的设问方式增加了试题的信息量，使试题变得复杂，其中暗含的数学知识需要学生准确理解并进行数学抽象，向学生提出了灵活思考、创新解法的挑战，学生需要将已经学习到的数学知识、数学思想及方法融会贯通，需要用不同以往的思维方式与方法去解决数学问题，这样的试题是学生所不熟悉的，便会阻碍其理解与解答，加大难度[5]．

试卷中新颖性试题的设置要考虑其对试卷难度带来的影响．以山西省中考数学试卷为例，整卷涉及到的情境非常丰富，有快递、黄河流量、传统优秀文化、高铁速度与时间、数学的发现，等等．例如，试卷中19题、21题、22题都比较新颖，既具有开放性，又考查学生的数学阅读理解能力，而且探究性也很强．然而这些题目同时出现在一份试卷中使得试卷综合难度过大．2018年山西省中考数学试卷的得分率为0.64，其得分率低的原因主要是试卷阅读量和试卷的新颖性过大导致试卷难度增加．

3.6 学生实际水平

学生的实际水平是影响数学试卷综合难度的关键指标．前文论述的5个难度指标属数学试卷的绝对难度方面，是客体自身所具有的，学生实际水平体现了试卷绝对难度的相对性，实践主体对难度的影响在此显现，主客体得以统一．可以说，学生的实际水平是检验、调整数学试卷绝对难度的量尺．

由于不同地区学生所处的地域文化不同，社会环境不同，教学条件、师资力量都不尽相同，学生所接触的信息有差异．在中考命题工作中为使考试更加适切，允许不同省份中考数学试卷不同，甚至同一省份内试卷也有所不同．事实证明学生实际水平指标在试卷综合难度中起到关键作用，选取2018年云南省、温州市两地区的中考数学试卷进行了对比．试卷信息见表10．

表10 云南省与温州市中考数学试卷信息对比

温州市数学试卷大题数量为24，小题数量为35，云南省数学试卷大题数量为23，小题数量为30，考试时间均为120分钟．云南省平均每题解答时间为4分钟，温州市平均每题解答时间为3.43分钟．可以看出温州市试卷较云南省试卷题量略大，学生解答每题时间相对较少．云南省试卷字符数为1 647，温州市字符数为2 029，相比之下温州市试卷阅读量较大．通过征求专家意见判断试卷中创新性试题占比，云南省没有创新性试题，温州市创新性试题占11%．两地预先设置的易中难比例均为7∶2∶1，试卷中试题难度分布比例相同．但温州市试卷与云南省试卷在题型顺序设置上是存在差异的，前文已有论述．从以上数据看，在前5个难度指标中，温州市数学试卷有4个指标难度均大于云南省试卷，据此可以判断温州市试卷较难，云南省试卷较简单．但两地2018年中考数学的学生测试成绩，温州市得分率为0.70，云南省得分率为0.54，与之前的判断大相径庭，原因除前文论述中题型顺序的差异外，另一主要原因就是学生的实际水平．可以看出，同样的试卷对不同水平的学生而言难度是不同的，这个不同也可以通过通常意义上的得分率反映出来，这也很好地说明了试卷难度的相对性，凸显了学生实际水平在试卷综合难度中的重要地位．

4 讨论与建议

数学试卷综合难度的内涵及指标体系的建构旨在为数学试卷的评估及命制提供参考．综上所述，数学试卷综合难度6个指标从整体着眼到局部关照，克服了内容难度和统计难度的片面性，整体地衡量数学试卷难度．6个指标涉及影响试卷难度的客观与主观方面，从关注考试结果的评价转向关注对命题、组卷的过程性评价．

根据数学试卷综合难度指标体系，在试卷难度评估、命题过程中综合考虑试卷客体与实践主体，以学生实际水平为核心，着力整体布局．题型的选择要顾及不同水平的学生，同时合理安排题型的呈现顺序，控制考试时间、题量．如果试题内容、题型较难，学生所花费的时间较多，可以考虑减少题量或延长时间；如果题量较大，试卷阅读量较大，学生在有限的时间内思维量、运算量增大，对试题难度分布的调控就很关键；而试卷中背景新颖、试题的创新也难以回避试卷阅读量的问题……总之，试卷难度的评估与预判要综合考虑6个指标．数学试卷的综合难度既可用于考试后对数学试卷难度的评估，同时也可用于考试前对数学试卷难度的预估．在考试前的命题、制卷过程中，由于学生的实际水平需要经过实际考试后才能分析得出，可以结合学生往年的考试得分预先估计，再与实际得分相比较分析确定，逐年积累经验．

研究阐述了数学试卷综合难度的内涵及其影响要素，从宏观上为数学试卷难度的评判构建了框架．后续将围绕每一指标是如何影响试卷综合难度的，影响的程度大小如何，如何构建刻画数学试卷综合难度的模型等问题展开研究．以期对基础教育阶段的试卷难度评估及考试命题工作提供具体的可操作性建议．

[1] 刘怡翔．关于科学技术发展定律的证明提纲——献给21世纪科学家的一份科学技术的哲学研究报告[J]．西安联合大学学报，2000（3）：3–7，45．

[2] 王后雄，汪永鑫．新课程下高考地理考试评价标准及试卷结构技术指标构想[J]．课程·教材·教法，2008，28（5）：70–75．

[3] 任子朝，陈昂，黄熙彤，等．高考数学新题型试卷质量分析研究[J]．数学教育学报，2019，28（1）：1–7．

[4] 冯天祥．数学教师的基本功：数学试题的编制[J]．课程·教材·教法，2006，26（12）：46–48．

[5] 浦高华，薛柯伟．谈高考化学试题题型与难度的关系[J]．课程·教材·教法，1994，14（6）：38–40．

[6] 昌国良．高考数学题的难点与教学导向[J]．课程·教材·教法，2007，27（5）：40–42．

[7] 吕世虎，孙学敏．中国与新加坡初中数学教材中概率习题的比较研究[J]．数学教育学报，2010，19（6）：70–73．

[8] 王后雄．高考命题公正的现实困境与两难选择[J]．教育研究，2008，29（8）：24–31．

[9] 任子朝，陈昂，赵轩．加强数学阅读能力考查 展现逻辑思维功底[J]．数学通报，2018，57（7）：8–13．

[10] 国家教委考试中心数学试题评价组．数学试题评价报告[J]．课程·教材·教法，1996，16（5）：11–14．

[11] 岳宝霞，苏颖，冯虹．题目难度和冗余信息对代数应用题信息区分策略影响的实验研究[J]．数学教育学报，2013，22（6）：32–36．

[12] 教育部考试中心．2000年全国普通高考试题分析[J]．课程·教材·教法，2001，21（3）：47–57．

[13] 吕世虎，王尚志，胡凤娟，等．《2017年普通高中数学学科教学与评价指导意见》解析[J]．数学教育学报，2017，26（6）：1–5．

[14] 张夏雨．基于关系—表征复杂性模型的有背景问题难度研究[J]．数学教育学报，2010，19（3）：46–49．

[15] 吕世虎，王积建．初中数学探究式教学的实验研究[J]．数学教育学报，2005，14（4）：35–38．

Conceptualizing and Constructing Indicators for Examining Item Difficulty in Mathematics Tests

LV Shi-hu1, YU Li-fang1, WANG Shang-zhi2

(1. College of Education, Northwest Normal University, Gansu Lanzhou 730070, China;2. Capital Normal University, Beijing 100048, China)

The difficulty of mathematics tests depends on objective and subjective aspects: The objective aspect refers to the difficulty determined by the content and structure of the test as an object, that is, the absolute difficulty; the subjective aspect refers to the difficulty determined by the level of the students as a practice subject, that is, the relative difficulty. The difficulty of mathematics tests is determined by the absolute difficulty and the relative difficulty together. Therefore, this study conceptualized the indicators for examining item difficult in mathematics tests and constructed it by analyzing part of the test items of the senior school entrance exam from the following aspects: The type and order of the test items, the number of test items and the test time, the distribution of the test difficulty, the amount of reading on the test, the originality of the test, and students’ competencies

mathematics test; test difficulty; factor composition

G632.0

A

1004–9894（2020）04–0001–06

吕世虎，于丽芳，王尚志．数学试卷综合难度的内涵及其指标体系建构[J]．数学教育学报，2020，29（4）：1-6．

2020–02–04

互联网教育数据学习分析技术国家地方联合工程实验室2019年校企合作项目——数学个性化推荐系统核心资源开发与应用研究（5009-0181）

吕世虎（1963—），男，甘肃平凉人，教授，博士，博士生导师，数学课程标准研制组、修订组核心成员，主要从事数学课程与教学论、数学教育史研究．

[责任编校：周学智、陈汉君]