基于改进K-均值聚类算法的合肥市电动客车行驶工况构建＊

孙骏 方涛 张炳力 李傲伽 朱鹤

（1.合肥工业大学，合肥 230009；2.安徽安凯汽车股份有限公司，合肥 230051）

主题词：合肥市 电动客车 行驶工况 改进K-均值聚类

1 前言

行驶工况是车辆能耗和续航测试的基础，是研究汽车参数匹配和能量管理策略的依据，具备典型的时域性和地域性特征。近几年，合肥市汽车保有量大幅度增长，交通情况显著变化。另外，电动公交车占营运客车的比例越来越大，运行覆盖的线路也越来越广。2011年，唐邦强等建立的合肥市纯电动公交车行驶工况（Hefei Pure Electric Bus Driver Cycle，HF-PEB-DC）[1]仅选取了18 路公交车作为研究对象，难以较好地反映当下合肥市电动客车的运行情况，需要重新构建合肥市电动公交车的行驶工况。

国内外学者采用K-均值（K-Means）聚类算法进行了区域性汽车行驶工况的研究[2-5]。伊朗科技大学的A.Fotouhi 等人采用K-Means 聚类算法构建了德黑兰市汽车行驶工况[2]；爱尔兰都柏林大学的JohnBrady等人基于K-Means 聚类算法构建了爱尔兰地区电动汽车的行驶工况[3]。曹正策等人采用K-Means 聚类法完成了武汉市电驱动机械式自动变速器（Electric-drive Mechanical Transmission，EMT）纯电动公交车行驶工况的构建[4]；李耀华等人采用K-Means 聚类算法完成了西安市纯电动城市客车行驶工况（XiBUS）的构建[5]。传统的K-Means算法需要人工指定K值（分类数）和初始聚类中心点（中心的一般采用随机数），如果选择不当，往往会导致聚类的结果陷入局部的最优。另外，文献[1]、文献[4]、文献[5]关于电动公交车的行驶工况构建只选取了1条路线，存在一定的局限性。

本文选取合肥市4 条典型线路的12 辆电动公交车进行连续一周的数据采集，基于短行程分析法分割有效数据，采用主成分分析法和改进的K-Means算法进行分析，依据类中心距离选取类代表短行程，构建出合肥市电动客车的行驶工况。最后，将聚类的结果与其他线路采集的数据及国内外典型行驶工况进行对比。

2 准备工作

本文采用图1 所示的流程进行合肥市电动客车行驶工况的构建。

图1 车辆行驶工况构建流程

2.1 确定采集路线

截止到2018年2月，合肥市城市客车的行驶线路达236条，营运线路总里程达3 787.3 km，为了减少处理的数据量，参考相关工况建立过程，选取3～4 条典型公交线路进行工况的构建[6-8]。

筛选的原则是在尽可能覆盖所有典型路段的基础上选取分布最广、客流量最大的线路，涵盖拥堵的市中心、火车站，以及交通顺畅的郊区、城市高架、快速路等。

参照合肥市公交线路运行图，综合考虑线路的运行时间和间隔、组成特征和分布情况，选取了以下4 条公交线路：

a.B1 路，合肥市最早开通的快速公交线路，南北走向，经过市中心，客流量大。

b.18路，合肥市最早开始纯电动客车示范运行的线路，途径政务区，部分路段为快速路、支路和次干道，是合肥市西北部地区的典型公交线路。

c.137 路，路线相对较为偏僻，但也途径火车站、合肥工业大学屯溪路校区，为合肥市东北部地区从市中心到郊区的典型公交线路。

d.226路，合肥市最拥挤的路线之一，从火车站出发，途径市中心、中国科学技术大学抵达大学城，该线路高校学生较多，出行需求很高，另外，明珠广场站是合肥市西部的交通枢纽，客流量极大。

上述线路的基本情况如表1所示。

表1 选中线路的基本情况

2.2 数据采集装置

现有的公交车已装有车辆数据采集装置并部署了云端的实时监控和储存系统，每隔10 s输出一次状态信息，因其采集频率过低，必须添加额外的传感器获取所需数据。

本文通过布置高精度差分GPS设备的方法获取汽车行驶速度和定位信息。选用北斗星通公司的实时动态（Real-Time Kinematic，RTK）定位接收机，如图2所示。

图2 数据采集装置

搭配定位基站后，该接收机每秒可以输出5次厘米级定位信息和速度信息。考虑到数据量过大对后续的处理不利，同时参考国内外汽车行驶工况的建立过程，将GPS的输出频率设置为1 Hz。

3 采样数据的处理

3.1 数据融合及清洗

采集的数据有2个数据源，分别为公交公司云端监控平台获取的频率为0.1 Hz 的数据和高精度GPS 输出的1 Hz的数据。前者包括车辆ID、车速、时间、经纬度、站点、转向盘转角和荷电状态（State Of Charge，SOC）等信息，后者通过串口输出时间、车速、经纬度、定位精度等信息。

高精度GPS 定位设备在使用过程中会出现空值输出问题、丢星问题和静态偏移问题。云端监控储存的信息是从CAN总线读取的，其来源是汽车的传动系统，抗干扰性较GPS 设备高。因此，在两个信息源数据读取时，以云端监控获取的数据为基础，按时间顺序将GPS设备输出的速度和加速度信息以插值的形式插入云端监控储存的数据完成数据融合。

考虑到数据采集和传输过程中可能的异常，参考国内的相关文献和国外全球统一轻型车测试程序（World Light Vehicle Test Procedure，WLTP）对异常数据的处理方法，以加速度绝对值大于4 m/s2为标准寻找数据尖点，并根据情况对速度进行平滑或删除[6]。若采集的数据发生缺失且缺失时长小于3 s，则保留此段行程并进行插值，否则删去这段短行程。除异常值、缺失值外，还存在相同时间下出现2 个不同数值的情况，即“重复值”，对此，本文取重复值的均值。经数据处理，共获得15 809 669条数据。

3.2 短行程分割及特征参数计算

如图3 所示，汽车行驶过程中的短行程是指2 次怠速之间的运动行程[9]。经过算法分割，短行程数量为25 430个。

图3 某典型短行程工况示意

在进行工况构建时，需要用一些特征参数描述短行程的特征，如表2所示。

表3 定义了11 个用于评价聚类结果的统计学特征参数。

表2 短行程描述性特征参数

表3 短行程统计特征参数

3.3 主成分分析及降维

在经过原始数据的融合、清洗、短行程划分、特征参数计算并按预设规则筛选后得到24 595 条满足要求的19维数据。由于此时的数据量较大且维度较高，直接聚类会出现计算量大、聚类效果差等问题。实际上，在19个特征参数中，部分特征参数间存在一定的关联性，如平均加速度和加速时间、减速时间决定了平均减速度。因此须对原数据进行一定程度的处理，再进行聚类。

基于主成分分析的数据降维的具体实现过程为：a.对数据进行标准化并计算数据协方差矩阵，标准化后的数据矩阵记作Z。

b.计算协方差矩阵的特征向量和特征值，降序排序后的特征值记为λ1、λ2、……、λm，其中m为矩阵Z的维度，排序后的特征值记为V。

c.通过特征值计算主成分中各向量的贡献率p1、p2、……、pm和累计贡献率。主成分贡献率是指该主成分的方差在所有主成分的总方差中的比值。第i个向量的贡献率pi为：

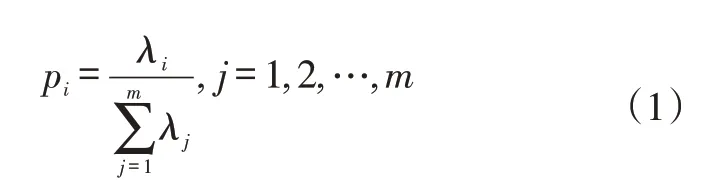
因前文已将特征值排序，这里只需要将计算出的贡献率进行累加即可计算出前i个主成分的累计贡献率Pi：

d.根据定义的累计贡献率限值选择主成分。参考相关文献[4，6，10-11]，一般累计贡献率取80%～90%，这里选择累计贡献率大于80%的k个主成分：

e.计算主成分得分。取V中的前k行向量组成矩阵Vk，由Z×Vk得到主成分得分。

f.保存降维结果和对应的短行程特征值。

前8 个主成分的贡献率及累计贡献率如图4 所示，由图4可知，主成分1～4的累计贡献率为80.66%，因此，可将19维数据降至4维。

图4 部分特征值主成分贡献率及累计贡献率

3.4 基于改进K-Means算法的数据聚类

K-Means 算法受K值和初始聚类中心点的影响极大，合适的聚类簇数和聚类中心点的选择十分困难[10]。为了减少初始聚类中心点的影响，引入二分K-Means算法。二分K-Means 算法是对K-Means 算法的优化，其基本思想是将原始簇一分为二，通过引入评价函数平方误差和（Sum of Squared Error，SSE）来评估聚类结果和指导下一步的二分，直到使得聚类的簇数等于设定的初始值[12]。平方误差和的计算公式为：

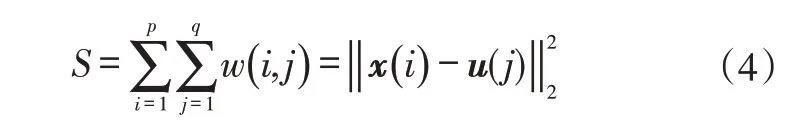
式中，S为平方误差和；p为簇的个数；q为样本点的个数；u（j）为第j簇的中心向量；w（i，j）为第i个样本点与第j个簇中心的欧氏距离。

这种二分K-Means 算法改进了原有的由程序随机或者由用户指定初始中心点的局限，通过对数据的循环二分聚类选取中心点，使得各中心点的特征不同，避免初始聚类中心点的“集聚”，减小局部最优的概率。当然，K值依旧需要用户自行确定。

实际上K值的选取具有典型的肘部特征，随着K值的增加，平方误差和的下降速度会在某个临界点后趋于平缓，该临界点往往被认为是“理想的K值”。

本文基于“肘部法则”对二分K-Means 算法进行改进，定义平方误差和的下降比例dSSE为：

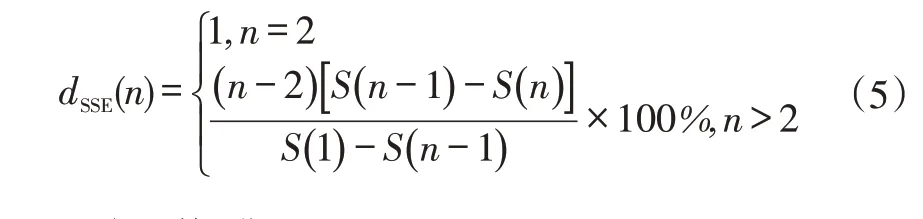
随着n的增大，dSSE小于预设值，即认为此时的n为最优的K值。为了避免簇数超出设定的允许值M，如n≤M-1时均未找到期望的临界点，则取M作为最优的K值，此时算法的效率最低。

基于“肘部法则”改进K-Means 的输入为不带分类标号的数据集X={x1，x1，…，xn}、最大聚类簇数M、预设的最小下降比DSSE，输出为“最优”K值、分类的标号、每一类的中心点、类内总距离，其流程为：

a.初始化。将目标簇数n初始化为2，运行K-Means 算法随机选择中心点，将数据分为2 个簇，并分别计算簇的平方误差和。

b.将聚类的目标簇数自加1，选择满足条件的可以分解的簇。选择条件主要是综合考虑簇的元素个数以及聚类代价即数据平方误差和。当某簇数据点的数量大于规定的最小数量，则认为该簇可以分解。

c.考虑到此时子簇的分解实际仍基于二分均值聚类算法进行，在对要分解的子簇进行分解聚类时，重复进行多次分解，取平方误差和最小时的分类结果作为当前分类次数的最优结果，计算并记录dSSE（n）和当前的聚类结果。

d.若dSSE（n）＜DSSE或K=M，则认为此时的K即为“最优”K值，此时的聚类结果为最优结果，则跳过步骤e，执行步骤f，否则执行步骤e。

e.若在近几次的二分聚类中dSSE（K）突然减小，则认为开始减缓的类簇数（K-1）和对应的聚类结果是最优的。否则，不断重复步骤b～步骤d。

f.输出“最优”K值、分类的标号，以及每一类的中心点和类内总距离。

基于上述流程，在Python平台编写改进K-Means算法，设M=10、DSSE=30%，运行程序。

3.5 聚类结果分析

表4 给出了基于改进K-Means 聚类后各簇的特征值。第1 类、第2 类的停车比例较大且平均速度较小、短行程时间较短，比较符合十分拥堵和一般拥堵的工况。第3 类、第4 类的停车比例较小且平均速度较快、短行程时间较长，比较符合通行正常和通行畅通的工况。由表4可知，合肥市的交通状况61%的时间较为畅通，一天当中有20%的时间处于拥堵状态，这比较符合上、下班高峰期（8：00～9：30、5：00～6：30）占公交车运行时间（一般6：00～22：00）的比例特征。

为了对比改进K-Means 和K-Means 算法的聚类结果，基于K-Means 算法，将聚类的目标簇数分别设置为2、3、……、10，将聚类后的平方误差和与基于改进K-Means算法结果进行对比，考虑到K-Means算法的随机性，将K-Means算法运行10次，以最小的平方误差和作为当前K值的结果。如图5所示，改进K-Means算法实现了自动识别基于“肘部法则”的最优K值，分类结果更理想。

表4 基于改进K-Means算法的聚类结果

图5 2种聚类算法的平方误差和

实际上，改进K-Means 算法的核心机制仍为K-Means 算法，基于二分思想，单步多次划分取最优解，降低其随机性，并取分割后平方误差和降低最大的簇进行划分使得算法在增加分类数的同时最大程度降低平方误差和。这些改进使得K-Means 算法的寻优不是通过漫无目的的多次运行，而是在有限次数的子空间内使数据沿着平方误差和下降速度“最快”的方向进行聚类。这使得改进的K-Means 和原有的K-Means 算法相比，虽然单次的运行时间长，但从聚类结果和运行机制来看，改进K-Means 比K-Means 效果更好。

4 城市客车行驶工况构建及对比

4.1 工况构建

依据类中心距离的大小选取各簇代表运动片段，从而构建车辆的行驶工况。参考相关工况，以及台架试验要求，将工况总时间设为1 500 s[4-5，13]。通过分类后各簇的样本数占总样本数的时间比例来确定各簇中抽取的片段数量，将选出的片段进行拼接，即可完成工况的构建。最终选取18条代表工况，循环工况时长为1 474 s，形成的合肥市电动公交车行驶循环（Hefei Electric Bus Cycle，HFEB）如图6所示。

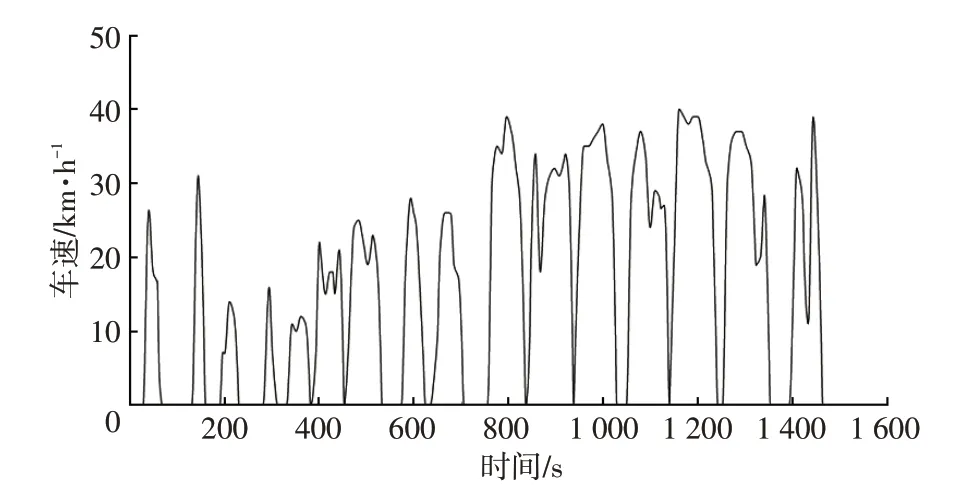
图6 合肥市电动客车行驶循环

4.2 工况验证

为了验证本文建立的行驶工况的代表性，随机抽取了合肥市30 路、902 路公交线路进行数据采集，将采集到的数据按前面的步骤进行处理，获得其短行程的特征值，将抽中的样本与用于构建工况的4条公交线路总样本、自建行驶工况及文献[1]建立的早期纯电动公交车行驶工况（HF-PEB-DC）的特征值进行对比。受篇幅所限，这里只比较统计特征值，结果如图7、图8所示。

图7 怠速、匀速、加速、减速工况分布情况对比

由图7、图8 可知，自建工况与30 路、902 路和原始数据均值间的误差较小，而HF-PEB-DC 在速度的分布比例上与当前的汽车行驶数据相比存在较大差异。因此，本文建立的行驶工况更能反映合肥市当前的道路交通情况。

图8 速度分布情况对比

4.3 典型工况对比

如表5 所示，将自建的HFEB 与纽约城市公交循环（The New York Bus cycle，NYBus）[14]、曼哈顿巴士循环（Manhattan Bus Cycle）[14]、中国城市客车行驶工况（CHTC-B）[15]、文献[4]建立的武汉EMT Bus Cycle、文献[5]建立的XiBUS、合肥公交车行驶工况[7]以及文献[1]建立的HF-PEB-DC 工况中的特征参数进行对比。

通过对比可知：

a.HFEB 与NYBus 工 况、Manhattan Bus Cycle 工况在平均速度、驻车情况、加速情况方面都存在较大的差异。

b.HFEB 工况与HF-PEB-DC 相比，最大速度和平均速度较低，表明合肥市整体交通运行情况较2011年差。这反映了城市工况时域性的特征，整体趋势符合合肥市近年来汽车保有量大幅增加、交通拥堵程度加深的趋势。同时，HFEB工况与HF-PEB-DC相比最大加、减速度增长，这说明近年来电动公交车的加速度性能较2011年的纯电动公交车好。

c.HFEB 工况与XiBUS 和武汉EMT Bus Cycle 在加速度、减速度、时间比例上差异较大，体现了城市工况地域性的特征。

表5 自建HFEB和国内外典型工况的对比

5 结束语

本文以合肥市4 条典型线路12 辆公交车连续一周的运行数据作为研究对象，通过数据的融合、清洗与分割得到25 430 个短行程片段，基于主成分分析和改进K-Means算法将数据聚类成4类，依据类中心距选取各簇的代表工况，构建了合肥市电动客车的行驶工况。

本文提出的基于“肘部法则”和二分K-Means 算法的改进K-Means 算法解决了需用户指定K值和聚类结果随机的问题，算法的速度较慢，但其构造出的车辆行驶工况比基于传统K-Means 算法的精度更高。本文构建的工况与国内外的工况存在显著差异，验证了工况的时域性和地域性特征。