利用混沌吸引子阶跃变化现象检测滚动轴承微弱故障

闫晓丽，唐贵基，王晓龙

(华北电力大学能源动力与机械工程学院，河北保定，071003)

在机械设备故障发生的早期，故障信号相对于噪声较为微弱。传统去噪方法在消除信号噪声的同时，有可能将表征故障特征的信号一同滤除，继而得出错误的检测结论，因此，传统故障检测方法对被检信号的信噪比要求较高，在早期微弱故障检测的应用中受到了限制[1]。自20 世纪90年代以来，BIRX 等[2]将混沌振子用于微弱信号检测后，国内外学者针对基于混沌振子的微弱信号检测做了大量的工作[3-9]。混沌是服从确定性规律但具有随机性的运动，其随机性表现为初始条件和参数的微小差异有可能导致结果的显著不同，同时，混沌系统对噪声有较强的免疫性[10]。基于混沌振子的微弱信号检测正是利用混沌系统的参数敏感性和抗噪性，对淹没在背景噪声信号中的微弱信号进行检测。此类方法不是通过消除或抑制噪声来提取微弱信号的特征，而是利用非线性系统本身特性，在强噪声背景下检测微弱信号成分[5]。目前，应用于微弱故障诊断的混沌振子类型有Duffing 振子[6]、Lorenz 振子[7]以及一些耦合混沌振子[8]。这些检测系统大多是利用参数改变使混沌状态发生变化的原理进行设计的。基于混沌振子的微弱信号检测方法关键在于混沌状态判断和阈值选取[9-13]，目前，人们主要研究混沌状态与周期状态转变的判断方法[14-17]，关于混沌状态之间或周期状态之间的转变过程的研究较少，而且现有混沌状态判据仍存在定性混沌判据计算过程复杂，运算时间长，定量混沌判据的混沌状态的临界点难以确定，阈值选取不够精确的问题[18-20]，难以在工程实际中应用。因此，研究简单有效的混沌振子状态变化判据和阈值选取方法，对提高基于混沌振子的微弱故障信号检测方法性能具有重要意义。本文作者首先分析典型的混沌系统的吸引子形状的阶跃变化特性；然后在吸引子形状阶跃变化的基础上，提出自适应选取阈值方法和自动判据混沌吸引子阶跃变化的方法，并设计基于混沌系统吸引子阶跃变化的微弱信号检测系统；最后通过对仿真信号和实测滚动轴承的微弱故障信号的检测实验，验证了方法的有效性。

1 混沌振子吸引子阶跃变化现象

在整数阶混沌系统中，一些特定参数为临界值时，混沌吸引子与其吸引盆边界接近重合，吸引子的相图会发生明显变化，转变为另一种稳定的周期状态或另一形式的混沌[12]，因此，混沌系统吸引子形状的变化不仅发生在混沌状态与周期状态的转化过程中，而且系统由周期状态向另一周期状态或从一种混沌状态向另一种混沌状态转变同样可能引起系统吸引子形状变化。吸引子的变化是由系统状态变化引起的，能够反映参数的变化。本文通过研究Duffing 和Lorenz 这2 类典型的混沌振子的吸引子阶跃变化现象验证这一结论。

1.1 Duffing振子的吸引子阶跃变化现象

Duffing 振子是目前应用最为广泛的混沌振子微弱信号检测系统，其动力学状态方程为

式中：k为阻尼系数；ax + bx3为恢复力项，x为状态变量，a 和b 为系数；f cos(ωt + φ)为强迫项，f为强迫项幅值，ω为强迫项角频率，φ为强迫项初始相位；W为输入信号的加权因子；s(t)为输入信号。参考关于Duffing振子的文献[8-11,14-16]，设定系统的参数为k = 0.5，a = -1，b=1，ω=1 rad/s，φ= 0。系统处于无输入信号的状态。求解得到状态变量x随f变化的Duffing系统局部分岔图，结果如图1所示。

由图1 可知：Duffing 振子是由倍周期分岔通向混沌的。在参数f变化的过程中，Duffing系统在0～f1之间为同宿轨道，在f1～f2范围内经历了倍周期分岔的变化，过渡到f2～f3范围内的混沌状态，随后周期、混沌等多种状态交替出现。在分岔图中，可以观察到状态变量x 在f2前后发生了明显阶跃性变化。

图1 Duffing振子分岔图f ∈[0,1]Fig.1 Bifurcation diagram of Duffing oscillator f ∈[0,1]

图2 Duffing振子x-y相图Fig.2 x-y plane of Duffing oscillator

Duffing 振子x-y 相图如图2 所示。由图2 可知：参数f在由0逐渐增大至0.382的过程中，状态变量x 的值域未发生突变，x-y 相图未发生明显变化；当f 由0.382 增加到0.383 时，x-y 相图显示出Duffing 振子的吸引子形状发生了明显变化，状态变量x的值域出现了阶跃性变化。因此，可以通过观察Duffing 振子吸引子发生了阶跃变化，得出混沌系统的参数发生变化的结论。将Duffing 振子吸引子的形状变化作为待测信号存在同频谐波信号的判断依据具有可行性。

1.2 Lorenz振子的吸引子阶跃变化现象

Lorenz 系统为典型自治混沌系统，不显含时间和频率。利用文献[13]提出的非共振参数周期信号强迫Lorenz 系统，控制混沌状态变化思想，设计基于Lorenz振子的微弱信号检测模型如下：

式中：1+ f cos(ωt + φ)为强迫信号。对于Lorenz系统，多数研究设定a=6.4，b=8/3，当0 ＜c ＜1时，系统稳定于原点；当1 ＜c ＜24.74时，系统处于不稳定状态；当c ＞24.74 时，系统处于稳定的混沌或周期状态[19]。因此，设定Lorenz系统参数为a=6.4，b=8/3，c=25.4，ω=60 rad/s，考虑输入信号s(t) = 0。图3 所示为变量x 随参数f 变化的Lorenz振子局部分岔图。由图3可知：随着参数f的变化，状态变量x的值域发生了几次明显的阶跃性跳变。

图3 Lorenz系统局部分岔图f ∈[0,1]Fig.3 Local bifurcation diagram of Lorenz system f ∈[0,1]

Lorenz振子x-z相图如图4所示。由图4可知：参数f 在临界点f =0.149 的前后变化时，Lorenz 振子的x-z相图的混沌吸引子形状发生了较明显的变化，Lorenz 振子的吸引子的变化同样具有参数敏感性，因此可以将Lorenz 振子吸引子的阶跃变化作为待测信号存在同频谐波信号的判断依据。

图4 Lorenz振子x-z相图Fig.4 x-z plane of Lorenz oscillator

对2类典型的混沌系统的动力学特性进行分析后发现，随着特定参数的变化，当参数超过某一临界值时，Duffing 振子和Lorenz 振子都存在吸引子发生阶跃变化的现象，可以通过观察吸引子发生阶跃变化判断系统参数发生变化。这一结论为基于混沌吸引子阶跃变化的微弱信号检测方法的可行性提供了理论支持。

2 微弱信号检测方法

基于混沌吸引子阶跃变化的微弱信号检测分为3个阶段：第一阶段是混沌系统选取，即选取合适的混沌振子，设计相应信号检测系统；第二阶段是系统调整，即确定阈值将系统调整到某一临界状态；第三阶段是输入待测信号，选取合适的判断依据，判断待测信号成分是否存在。具体检测流程如图5所示。

图5 检测流程图Fig.5 Detection flow chart

在第一阶段，选取混沌振子。根据混沌振子的动力学特性，确定固定参数与变化参数后设计相应的微弱信号检测系统。然后对待测信号进行预处理，为避免含噪信号对检测系统的影响，利用待测信号的最大瞬时幅值预估待测信号强度，将信号进行归一化处理，与加权因子结合，使信号强度降低到0.01 W以下。

在第二阶段，调整系统。由于强迫力的频率变化对系统的动力学特性影响较明显，因此采用固定强迫力频率，引用变尺度的思想对待测信号进行时间尺度或频率尺度的缩放，变尺度是在不改变信号离散数值的前提下，在时间或频率轴上重排待测信号[14]，将高频信号转换为任意频率的低频信号。然后在当前参数条件下确定临界状态的阈值。最后调整系统处于临界状态。

在第三阶段，将预处理后的待测信号输入检测系统中，根据吸引子的变化情况检测输入信号是否含有待测频率成分。若吸引子发生变化，可确定待测信号包含当前频率的谐波成分。

2.1 变尺度方法

设待测信号的角频率为ω1，采样角频率为ωs，则混沌振子数值计算的步长为2π/ωs。变换龙格-库塔数值计算的步长可以实现待测信号时标的扩张[14]，变换系数设为R，则计算步长为2πR/ωs。通过尺度变换可以将待测信号变化为频率为ω1/R 的信号，将信号输入处于临界状态的混沌振子中，若R = ω1/ω，则混沌阵子的吸引子会发生阶跃变化。由此可判断待测信号存在特定频率成分，待测信号频率ω1可通过强迫项频率ω 与R 的乘积获得。改变R可在固定强迫力角频率的条件下，检测信号是否含有待测成分。

2.2 阈值自适应选取方法

在实验过程中发现阈值的选取对检测结果的影响也比较明显，精度高的阈值能够提高检测系统的分辨力，但是，由于噪声的不确定性，在没有待测频率的信号时，强噪声也可能诱导混沌吸引子发生变化。在同等强度的噪声背景影响下，阈值的精度较高，其容噪性和保厚性都会下降，导致检测结果的正确率降低。因此，阈值选取需要满足所对应的混沌系统临界点的突变性和敏锐性，临界点的邻接区间必须保持一定的厚度，同时阈值也要有一定的容噪性[15]。目前大部分基于混沌振子的微弱信号检测都存在检测阈值难以确定的问题。本文以混沌吸引子的阶跃性变化作为判断依据，提出一种自适应选取阈值的方法。

以基于Duffing 振子混沌吸引子形状阶跃变化的方法进行微弱信号检测为例，参数选取与1.1节的相同。观察Duffing 振子的局部分岔图与图6 所示的吸引子形状发生阶跃变化前后时域波形图，发现当f=0.382时，吸引子形状没有发生明显变化，时域波形图中状态变量x 全部大于-0.2。而当f=0.383 时，吸引子形状发生明显阶跃变化，状态变量x有一部分小于-0.2，x的值域发生明显变化。

以此为依据，设计阈值自动选取方法。检测系统初始参数设置与1.1 节相同，阈值为fd。检测强迫力频率不等的待测信号的频率时需要对待测信号进行尺度变换，当变换系数R 超过一定范围时，待测信号的采样间隔和数值计算步长变化过大，有可能使检测振子的动力学特性发生变化，检测正确率也会下降。阈值自适应选取，由初始值开始，步长取2πR/ωs，增加参数f。用龙格-库塔法求解当前参数条件下的Duffing 方程，得到状态变量x解集。xd为判断吸引子发生变化的状态变量阈值，N为当前参数条件下，状态变量值域超过阈值连续出现的次数，M 为状态变量值域不超过阈值的状况连续出现次数。初始设定N=0，M=0，xd=-0.2。判断解集中是否有小于xd的x，若求解Duffing 系统有小于xd的x，则设定N=N+1，M=0；若没有，则设N=0，M=M+1。继续判断N 和M 是否满足都大于等于20，若满足，则f-20(2πR/ωs)可作为检测系统的阈值fd。实现自适应选取当前参数条件临界阈值，具体流程图如图7所示。

图6 x的时域波形图Fig.6 Time domain waveform of x

2.3 混沌吸引子阶跃变化自动判断方法

阈值确定后，将待测信号输入Duffing 微弱信号检测系统中，若含有与强迫力频率相同成分，则系统的吸引子形状发生变化。检测系统在临界状态时域波形图中，状态变量x 的取值都大于-0.2，超过临界状态，有一部分x 小于-0.2。可将-0.2 作为判断混沌吸引子发生阶跃变化的阈值xd。将待测信号输入微弱信号检测系统，判断状态是否有小于xd的变量x出现，用矩阵变量C表征对应混沌振子吸引子形状是否发生变化，若发生变化，则C(i) = 1，否则，C(i) = 0(其中，i 为混沌振子序列号)。建立待测频率与吸引子发生阶跃变化对应关系表，可直接给出判断结果。

2.4 检测盲区的消除

设f1为输入信号中同频谐波成分信号幅值，φ1为同频谐波成分信号初始相位，Δω= ω- ω1为强迫力与待测信号的频差。Δφ= φ- φ1为强迫力与待测信号的相位差。总强迫力为

图7 算法流程图Fig.7 Detection flow chart

其中：

Duffing 系统强迫力与参考信号相位差范围为[-arctan(Wf1/fd),arctan(Wf1/fd)]。由于加权因子的存在，强迫力的幅值f 远大于待测信号的幅值Wf1，因此待测信号相位对系统的影响可以忽略。

系统处于临界状态时，将fd代入式(4)得

只有当A(t) ＞fd时，混沌系统的吸引子形状才会发生变化。此时，Duffing 系统检测窗口为[-π + arccos(Wf1/(2fd)),π - arccos(Wf1/(2fd))]。为消除检测盲区，需对没有产生吸引子变化的输入信号进行系统周期强迫力移相π 后的二次检测[16]，确保不会出现因初始相位的不同产生的漏检现象。

3 仿真信号检测

根据基于混沌系统吸引子阶跃变化的检测方法的原理，若待测信号中含有强迫力同频成分，总的强迫力的幅值超过阈值引起系统吸引子形状发生突变。为验证该方法的有效性，利用如式(6)所示模型[17]模拟滚动轴承内圈早期故障，作为输入信号输入检测系统。

式中：s(t)为周期性成分；A0为其幅值，取值0.4；n(t)为功率可调整的白噪声，叠加噪声后信噪比为-43.6 dB；ωr为转动角速度，取值40π rad/s；Ca为衰减系数，取值500；ωn为共振角速度，取值为7 000π rad/s；特征频率为100 Hz，特征角频率为ωi=200π rad/s；τi为相对于周期T的第i次冲击造成的微小随机波动，服从标准差为5%ωr的正态分布；采样角频率ωs设106π rad/s。图8所示为滚动轴承内圈故障仿真信号波形及频谱，由于仿真轴承故障信号相对背景噪声较为微弱，图8(c)所示的频谱图中内圈故障特征频率并不突出，因此不能通过频谱分析判断故障类型。对仿真信号进行包络谱分析，如图9所示，未见明显的特征频率成分。

利用Duffing 和Lorenz 微弱信号检测系统对仿真信号进行检测，设置输入信号的加权因子W=0.005，2个检测系统的参数与第1.1节和1.2节中的一致。由于待测成分已知，将故障特征频率作为待测信号的频率，即ωi=ω1。可根据第2.1 节的尺度变换方法对待测信号进行变换。利用Duffing 系统检测内圈故障特征角频率的1 倍频和2 倍频时，R 分别设为623.319 与1 256.637；利用Lorenz 系统检测时，R分别设为10.472与20.944。在当前步长条件下自动选取阈值，将Duffing 和Lorenz 微弱信号检测系统调整到临界状态。将尺度变换后的s(t)输入各系统进行检测，图10～13所示为混沌振子的相图。

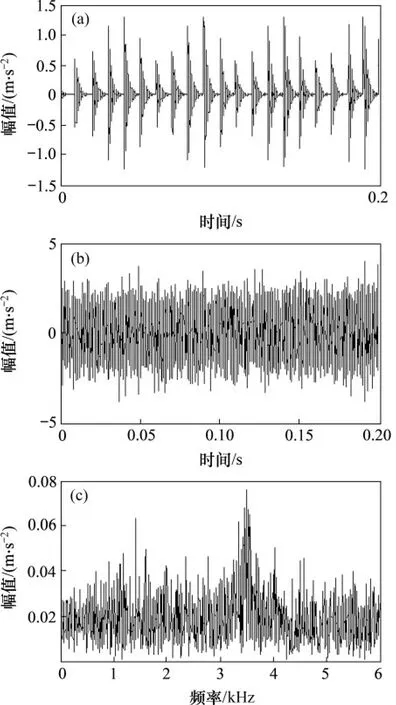
图8 仿真信号的波形及频谱Fig.8 Waveform and spectrum of simulated signal

图9 仿真信号的包络谱Fig.9 Envelope spectrum of simulated signal

用龙格-库塔法对各系统进行数值求解，得到状态变量的集合。在对输入Lorenz 系统的信号求解后得到关于状态变量x的解集后，去掉前期部分数据，判断剩下的解集中是否有超出阈值xd的解出现，Lorenz系统的xd=0。若有，则自动判定待测频率信号的存在。通过判断吸引子形状是否发生阶跃变化，判定待测信号是否含有特定成分。记录检测结果。表1 所示为Duffing 和Lorenz 系统的参数阈值设置与检测结果。

图10 Duffing振子x-y相图(R=623.319)Fig.10 x-y plane of Duffing oscillator(R=623.319)

图11 Duffing振子x-y相图(R=1 256.663)Fig.11 x-y plane of Duffing oscillator(R=1 256.663)

图12 Lorenz振子x-z相图(R=10.472)Fig.12 x-z plane of Lorenz oscillator(R=10.472)

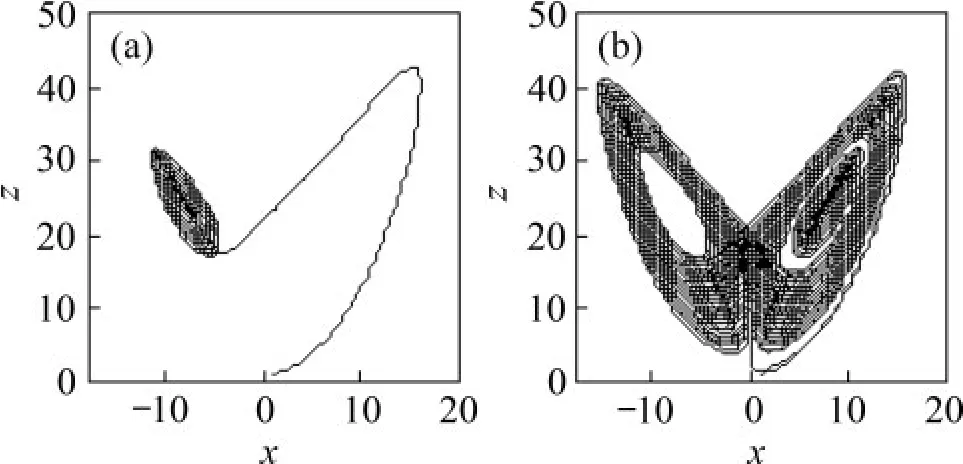
图13 Lorenz振子x-z相图(R=20.944)Fig.13 x-z plane of Lorenz oscillator(R=20.944)

表1 参数阈值设置与检测结果Table 1 Threshold and detection results for simulated signal

从表1可以看出：采用基于混沌吸引子的阶跃变化进行微弱故障信号检测，Duffing 系统和Lorenz 系统都能检测出滚动轴承内圈故障特征角频率成分。结果表明，Duffing 系统和Lorenz 系统在对不同频率的信号进行检测时的容噪性都比较稳定，检测正确率相对较高；Lorenz 系统的求解过程时间都比稍长，Duffing系统的求解用时较短。

4 实验信号检测

为进一步验证本文方法有效性和实用性，利用电火花分别在SKF6205 轴承外圈、内圈上人工植入深度为1.5 mm，宽度为0.2 mm 左右的微小凹痕，将故障轴承安装在QPZZ-Ⅱ实验装置上模拟滚动轴承早期微弱故障。利用电机带动传动轴模拟在轴承处于早期微弱故障状态下的机械运转情况，轴承转动速度为1 470 r/min。利用加速度传感器采集故障信号，采样频率为12 kHz。

表2所示为故障轴承的结构参数。计算可得在当前轴承参数与转速条件下滚动轴承外圈故障的征频率为87.8 Hz，滚动轴承内圈故障特征频率为132.6 Hz。

表2 故障轴承结构参数Table 2 Structural parameters of fault rolling bearing

4.1 外圈故障检测

分析归一化处理后的外圈故障信号，图14 所示为信号时域波形图与频谱图。由于轴承故障损伤相对微弱，频谱中没有发现与外圈故障特征频率相关的成分。外圈故障包络谱图15所示。可见，未发现突出的外圈故障特征频率，因此不能通过频谱分析和包络谱分析判断实测信号的故障类型。

图14 外圈故障时域波形图及频谱图Fig.14 Time domain waveform and spectrum diagram of outer race fault

图15 外圈故障信号包络谱Fig.15 Envelope spectrum of outer race fault signal

利用本文方法对实测信号进行分析，计算滚动轴承外圈故障的特征角频率约为551.8 rad/s，实验过程中发现Lorenz 混沌振子在检测高频信号方面表现出更好的容噪性，因此，选Lorenz 混沌系统作为混沌振子，系统参数与1.1节中的一致，利用自适应阈值选取方法确定阈值fd=0.149。将归一化后的信号进行R 尺度变换，R=ωi/60，为避免特征频率因轴承参数与计算精度等原因造成计算误差，外圈特征角频率ωi∈[ωi- 5,ωi+ 5]，使ωk+1= ωk+ 0.5，k 为检测振子序号，共20 个振子。在对外圈故障的特征角频率的2倍频进行检测时，ωi= 1103.6 rad/s，其他参数不变。Lorenz 混沌振子微弱信号检测系统调整到临界状态，将经尺度R 变换后的信号输入检测系统，步长为R/12 000。根据混沌吸引子的变化特点，若发生变化，则C(i) = 1，否则C(i) = 0。检测结果由吸引子形状随待测频率的变化曲线表示，如图16所示。

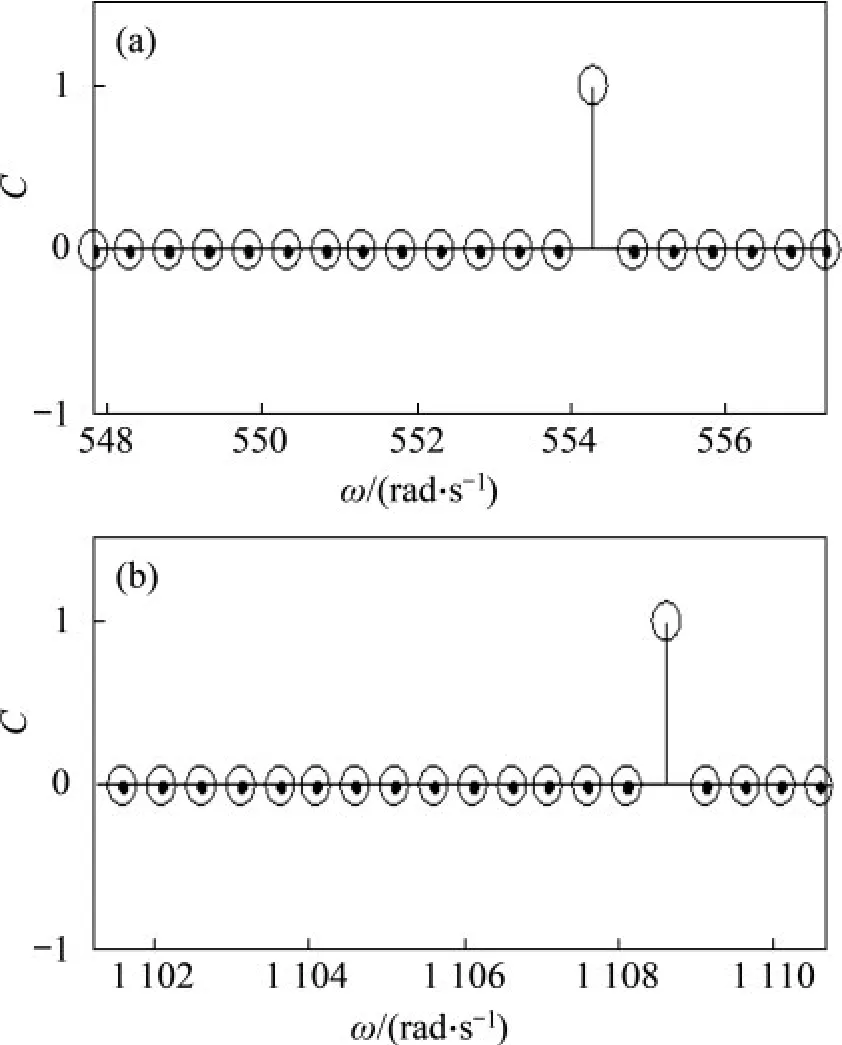
图16 外圈故障检测结果Fig.16 Detection results of outer race fault

待测外圈故障信号的特征角频率实测值约为554.2 rad/s，2 倍频约为1 108.6 rad/s。特征频率约为88.2 Hz 和176.4 Hz，在转速与环境等因素影响下，理论值与实测值有一定偏差。特征角频率的计算值与实测值非常接近，说明本文方法能够检测滚动轴承外圈微弱故障。

4.2 内圈故障检测

对内圈故障实测信号归一化后进行分析，图17 所示为信号的时域波形图与频谱图。可见频谱图中内圈故障特征频率同样不明显。图18 所示为内圈故障包络谱。可见，未发现含故障特征频率成分。因此不能通过频谱分析和包络谱分析判断实测信号的故障类型。

利用4.1 节的混沌振子对实测信号进行检测。经计算，内圈特征角频率约为833.2 rad/s，设内圈特征角频率取值为827.7～837.7 rad/s， 间 隔0.5 rad/s，共20个值，将归一化后的信号进行R尺度变换，R为ωi/ω。检测结果由吸引子形状随待测频率的变化曲线表示，如图19所示。

图19 内圈故障检测结果Fig.19 Detection results of inner race fault

经检测待测信号的故障频率约为834.2 rad/s，2 倍频约为1 668.2 rad/s。特征频率的1 倍频与2 倍频分别约为132.8 Hz和265.5 Hz，接近计算值。结果表明：本方法能够从实测信号中准确地检测出滚动轴承内圈故障的特征频率。

5 结论

1)随着参数的改变，Duffing 振子和Lorenz 振子都存在吸引子发生阶跃变化的现象。提出一种基于吸引子形状阶跃性变化的微弱信号检测方法。通过设计自适应的选取检测阈值方法和自动检测吸引子形状变化的方法，无需观察相图，自动判定信号中待测成分的存在。

2)本文方法能够有效检测滚动轴承微弱故障信号的特征频率成分，易于工程实现。为基于混沌系统的微弱谐波信号检测一种提供了有效的定量分析新方法，在微弱故障信号故障诊断中具有实际应用价值。