变桨对大型H型垂直轴风力机主轴偏振的影响

张立军，胡阔亮，顾嘉伟，朱怀宝，江奕佳，缪俊杰，李想，刘静

(中国石油大学(华东)机电工程学院，山东青岛，266580)

与其他能源相比，风能具有蕴藏量大、就地可取、分布广泛和不污染环境等优点[1]。中国是装机容量最多的国家，占比约36%[2]。现代风力机发展的主要趋势之一是大型化[3]，风力机塔架会越来越高，叶片展向长度越来越长，使得风剪效应对风力机的影响也越显著[4]，从而使叶片法向力载荷在展向方向呈不均匀现象[5]。目前，仍难以生产出商业化应用的大型垂直轴风力发电机，究其原因主要是很难解决气动效率、结构稳定性等一系列问题[6]。垂直轴风机旋转时载荷变化十分剧烈，造成机组振动和叶片连接件的疲劳问题十分突出。零件中缺陷随着风力机几何尺寸增大而增多，导致其疲劳强度降低，其中主轴作为风机内部关键的传动构件，工况复杂多变，工作应力变化幅度大[7]，容易造成损坏。垂直轴风力发电机由于气动特性和主轴结构的原因必须使用实时可变攻角技术和特殊塔架结构才能真正实现垂直轴风力发电机的大型化[6]。对于风力机主轴系统，国内外学者进行了很多研究。TAN等[8]建立风力机传动系统的三维动力学模型，研究了主轴悬置配置方式对传动系统动态特性的影响。SAIDI 等[9]提出了一种基于谱峭度数据驱动的风力机主轴轴承振动预测和健康监测方法。张婷婷[10]针对垂直轴风力机主轴结构特点，采用多岛遗传算法对其结构进行优化设计。刘瑞姣[11]对轴系结构进行了动力学模态分析，确定了临界转速，有效避免共振。目前对于垂直轴风力机，变桨技术主要用于当风速超过生存风速后调节叶片攻角实现风轮限速，已经在很多小型垂直轴风力机中实现商业化应用。同时，一些学者对变桨技术在稳定功率和提高风能利用率等方面进行了大量研究。KJELLIN 等[12]针对200 kW的大型风力机采用被动失速控制代替机械控制，如桨矩角调节控制以保持风轮转速恒定。GUO等[13]通过拟合桨矩角调节规律并控制叶片桨矩角变化以维持垂直轴风力机恒功率输出。李志萍[14]分析了MW 级风机的气动特性，阐述了液压变桨距系统的组成和工作过程，对液压变桨距控制技术展开深入研究。孔屹刚等[4]提出采用独立变桨方法以减轻风剪效应和塔影效应对水平轴风力机载荷和功率的影响。可见，为了延长主轴及相关部件的寿命，国内外学者多是从提高风能利用率或者稳定功率的角度来应用变桨技术，或者针对风力机主轴结构进行相关研究，但针对实时变桨技术对主轴的影响的研究较少，尤其是对基于风剪效应下的大型垂直轴风机主轴偏振效应的研究更少。本文作者将分析风力机在运转过程中主轴合成力的振荡程度，并研究实时变桨对主轴偏振效应的影响，为垂直轴风力机进一步实现大型化规模化发展提供理论参考。

1 风机主轴偏振效应机理分析

1.1 模型建立

大型H型垂直轴风力机模型如图1所示，叶片翼型选用厚度适中的NACA0015 对称翼型，其具体参数[15]如表1所示。

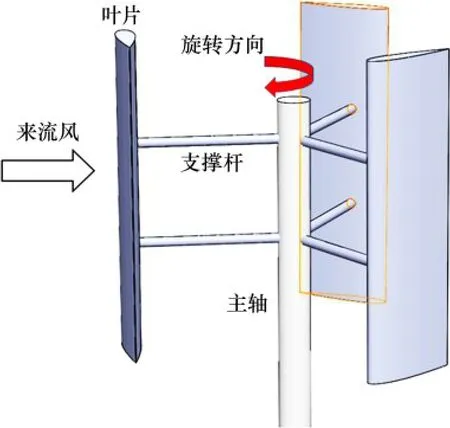
图1 H型垂直轴风力机模型Fig.1 Model of VAWT

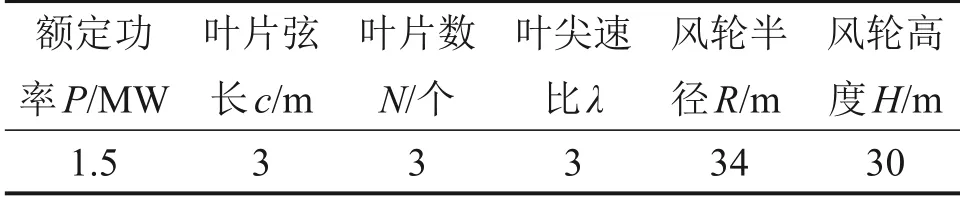
表1 垂直轴风力机相关参数Table 1 Parameters of VAWT

DMST模型计算精度较高，是研究垂直轴风力机的主要理论分析模型[16-17]。双致动盘多流管理论计算模型如图2所示。从图2可知：风轮旋转域被均分为上风向和下风向串联的制动盘。穿过旋转平面的流场被分为若干流管，每个流管的宽度为B，可将每个流管的气动计算视为相对独立[1]。θ为叶片所处方位角，θ=0°～180°时为上风区，其余方位角时为下风区，ω为风轮旋转时的角速度。可以通过迭代计算求得垂直轴风轮上、下风区的诱导速度和转轴处的诱导速度之间计算关系如下：

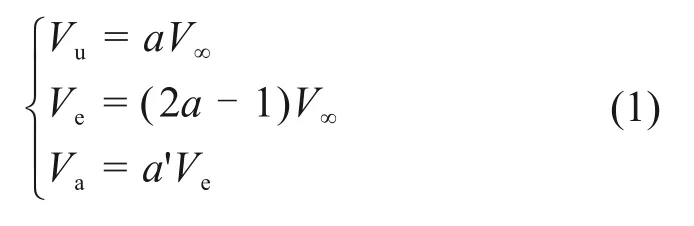
式中：Vu和Va分别为垂直轴风轮上、下风区的诱导速度；Ve为转轴处的诱导速度；V∞为来流风速；a和a'分别为上下风区诱导因子。

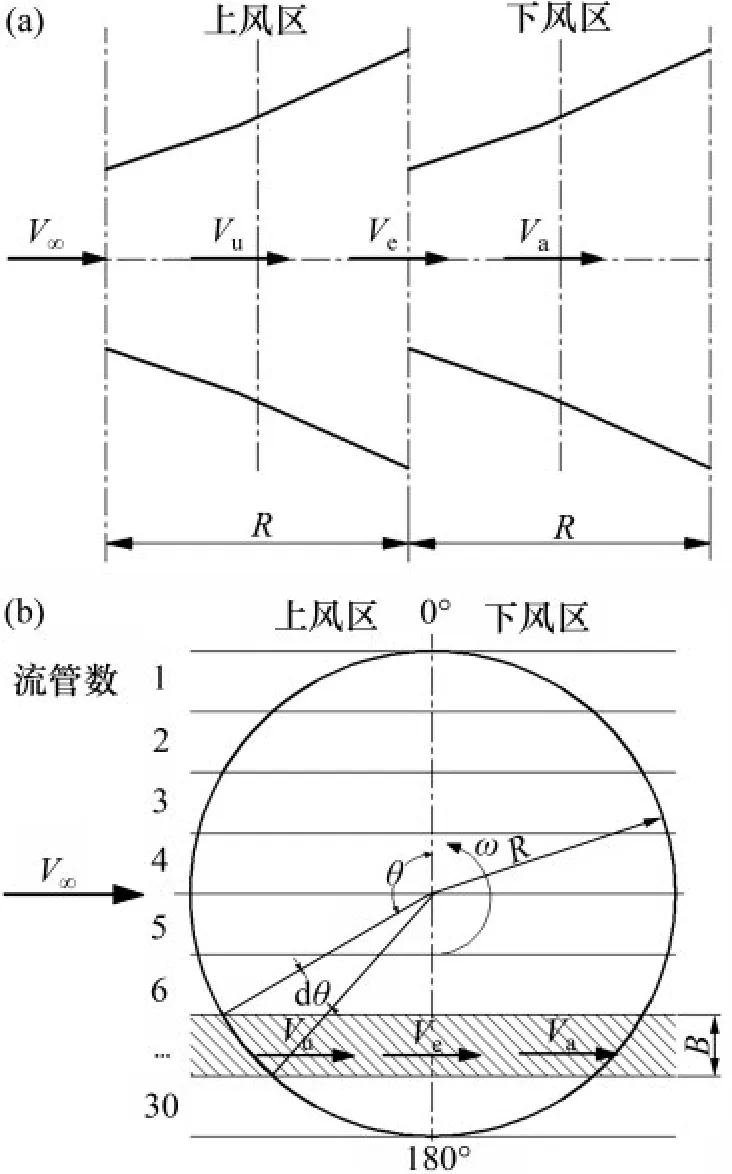
图2 双致动盘多流管理论计算模型Fig.2 Calculation model of multiple stream-tube&double actuator-disk theory

1.2 偏振效应机理分析

对垂直轴风力机叶片在上下风区的受力情况进行气动载荷分析，如图3所示。其中：W为合成风速；α为叶片攻角。

风轮旋转1周过程中，计算得到上风区诱导速度Vu和下风区诱导速度Va，并以上风区为例，结合图3 分析得到上风区攻角α、桨距角β 和上风区合成风速W与方位角θ之间的关系表达式：

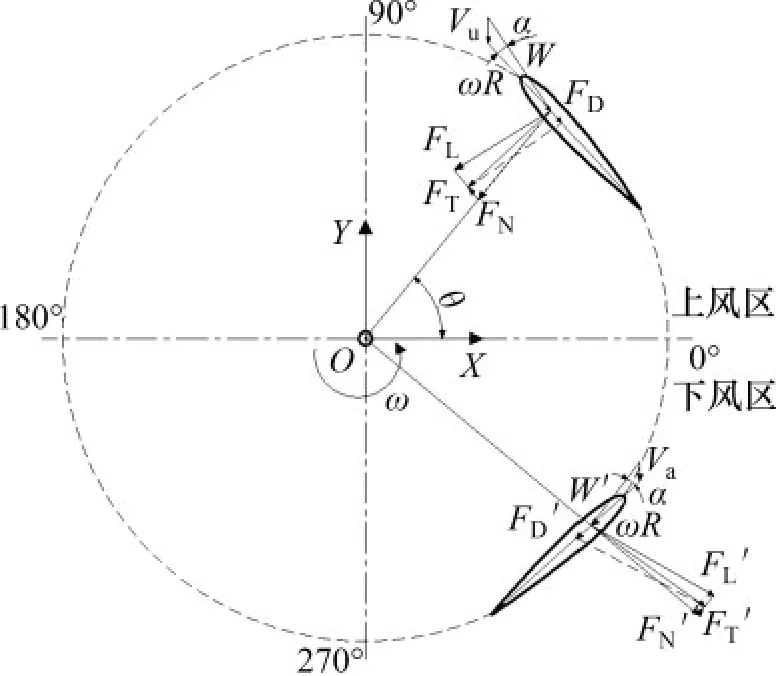
图3 叶片受力分析图Fig.3 Force analysis diagram of blades

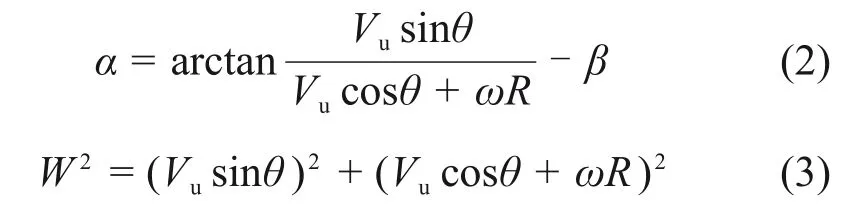
气流对叶片的作用力可分解为升力FL和阻力FD：

式中：ρ 为标况下的空气密度，为1.293 kg/m3，CL和CD分别为翼型升力系数和阻力系数。

结合图3所示叶片受力分析，得到推动风轮旋转的切向力FT和法向方向的分力FN分别为：

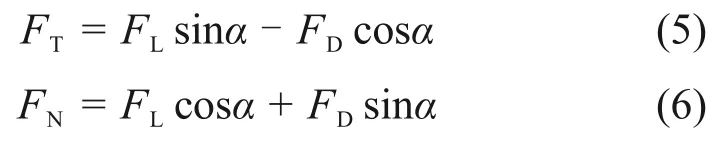
以叶片1为例，将其所受的切向力和法向力分解到X方向和Y方向，得到分力Fx1和Fy1：

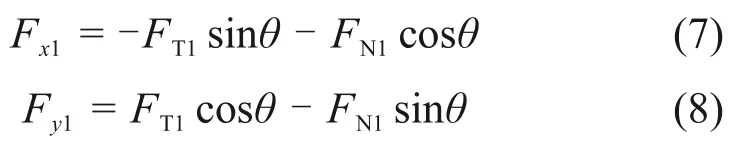
本文研究的风轮叶片数量为3，分析可得其余2 个叶片所受到的X 方向和Y 方向的分力与叶片1受到的分力相位差为120°，分别为X 方向分力Fx2和Fy2以及Y 方向分力Fx3和Fy3，最后将3 个叶片的分力合成得到风轮主轴所受的合力F：

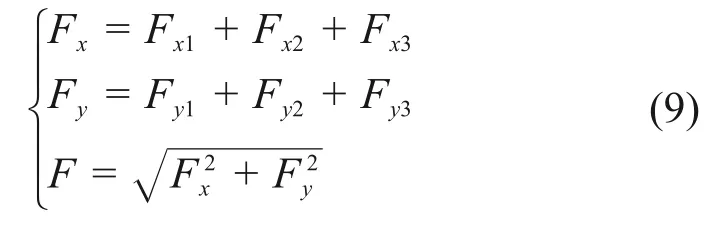
2 主轴偏振效应效果分析

利用DMST 结合图3 所述主轴偏振效应机理，计算得到垂直轴风力机在风剪效应下叶片所受气动力，并将其分解到X和Y方向上，最后合成到主轴上得到合成力，研究主轴合成力振荡情况。

2.1 风剪效应

风剪效应是指在大气边界层中风速随垂直高度的增长而增大的现象，对于大型风力机的计算结果影响显著[18]。考虑风剪效应时风速计算常用指数模型[19]如式(10)所示：

风轮在不同高度的风速如图4所示。从图4可以看出：风速随高度的增加呈指数型增长，并在风轮底部高度Z1和顶部高度Z2之间增长趋势明显，风速最大差值可达4 m/s左右。

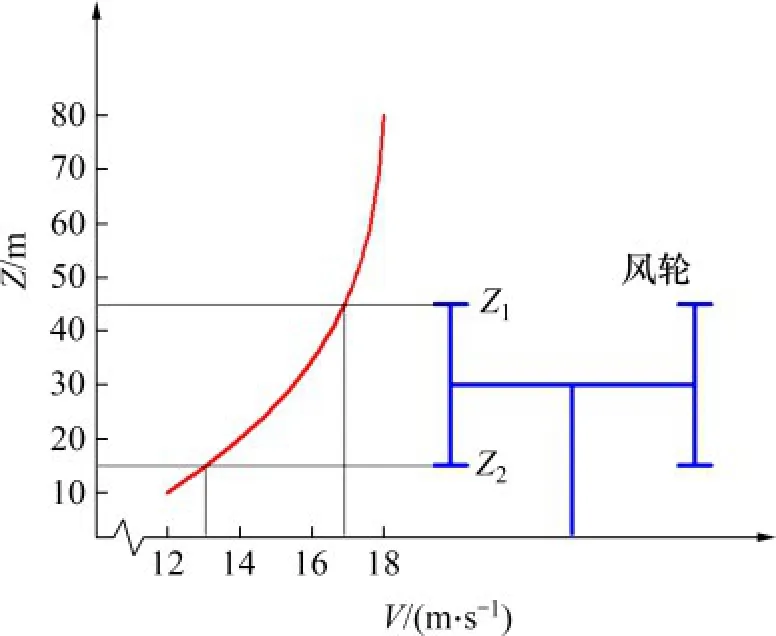
图4 风剪效应示意图Fig.4 Schematic diagram of shear effect

2.2 计算结果分析

将叶片以Δh=0.1 m 为间隔分成多段，在高度15～45 m 之间，控制风速以式(10)变化，并假设每段风速相同，每段之间的气流互不干扰。设定流管数为30，风轮每旋转6°时，计算得到3个叶片所受的升力和阻力，并将其分解到切向方向和法向方向得到切向力FT和法向力FN，最后将气动载荷在X 和Y 方向上的分力合成到主轴得到合成力F，计算结果如图5 所示。从图5 可以看出，在X 方向和Y方向，相邻叶片分力的相位差均为120°，其主轴合成力在风轮旋转1周过程中波动较剧烈，且呈现周期性变化，最大极差值为62 kN左右。

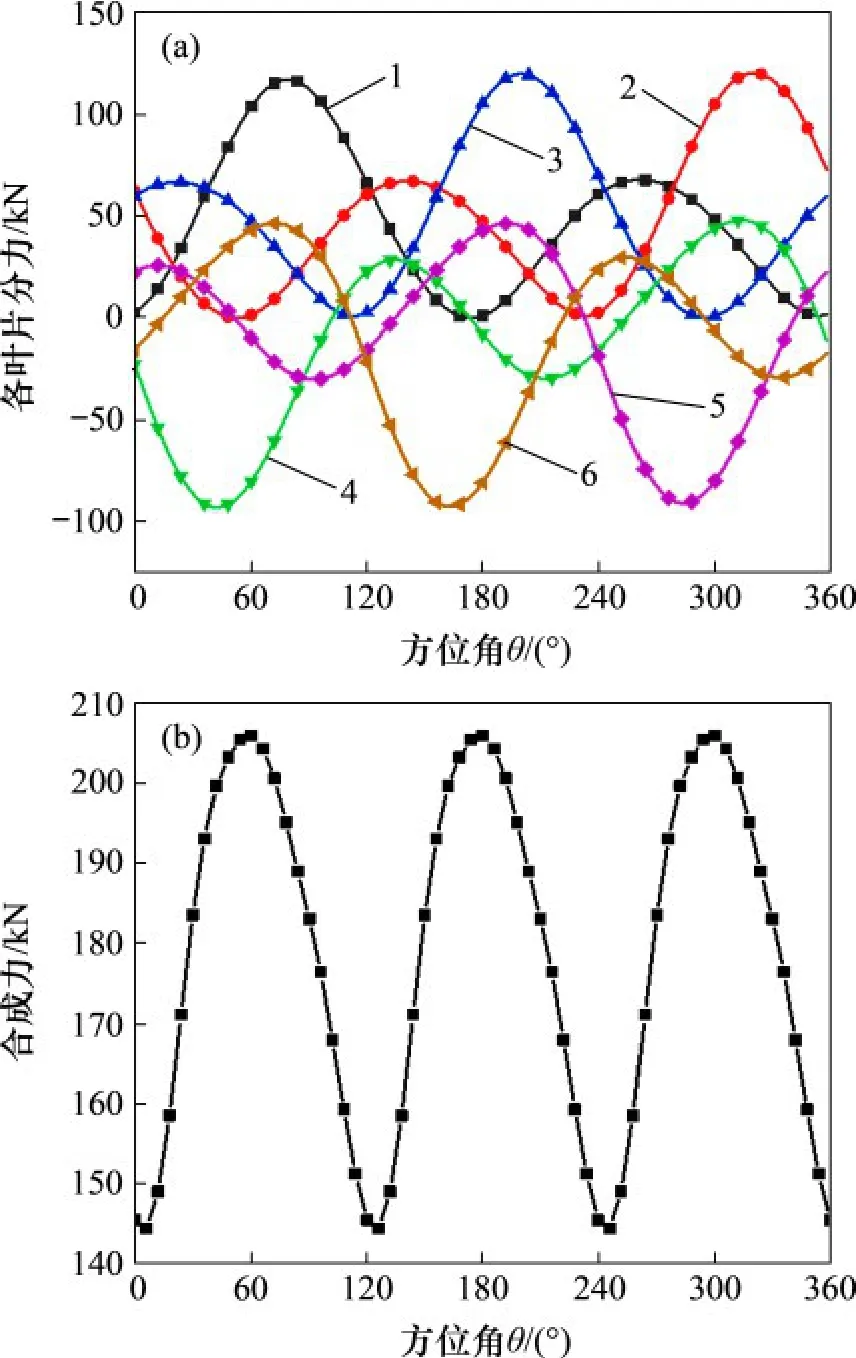
图5 主轴合成力振荡图Fig.5 Analysis diagram of synthetic force of main shaft

2.3 模型准确性验证

利用某垂直轴风力机[20]的试验数据对DMST模型进行准确性验证，为方便与试验数据直接对比，选取切向力系数CT作为准确性验证的指标，CT的表达式如下：

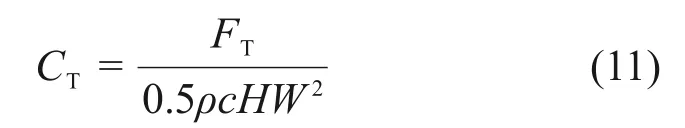
图6 所示为计算结果与试验数据的对比曲线。从图6 可以看出：计算结果总体略高于试验数据，造成这种误差的原因主要是由于DMST 模型是基于理论推导和经验总结的计算模型，在计算中假定了诱导速度方向不变，同时忽略了塔架、支撑杆以及叶尖涡效应等因素对风力机运转过程所造成的影响。但图6中DMST计算结果与试验数据整体趋势是一致的，理论计算与试验得到的最大切向力系数均发生在θ=90°左右，均在θ=180°左右时达到最低值，且两者相差较小。因此，将采用相同的DMST模型进行下一步研究。

图6 切向力系数对比Fig.6 Comparison of tangential force coefficient

3 实时变桨规律分析

基于上述主轴偏振效应分析，风力机主轴在任意时刻所受的合力不同的主要原因在于叶片在旋转过程中所受的气动载荷始终是变化的。为减小叶片气动载荷变化幅度，应使叶片攻角尽可能保持一致。利用DMST 以获取最大切向力系数为目标，计算攻角的最佳理论值，并制定变桨规律，尽可能使得风轮在旋转过程中维持在最佳攻角处，保证风轮旋转过程中获得较大切向力的同时减缓叶片所受气动载荷的波动情况，从而降低合成力振荡对主轴偏振的影响。

3.1 叶片理论最佳攻角计算

式中：N为叶片数；S为风轮的扫掠面积，m2。

由式(12)可知：当其他参数保持不变时，切向力FT达到最大时，Cp也为最大值。切向力FT可表示为：

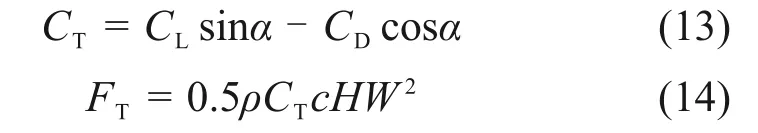
其中：切向力系数CT是升力系数CL与阻力系数CD在弦长方向的合成值，它们之间的关系如图7 所示。本文风力机模型运行时雷诺数Re=2.4×106。将翼型静态升阻力系数[3]插值并结合式(13)可以得到Re=2.4×106时的升力系数CL、阻力系数CD与切向力系数CT随攻角α的变化曲线，如图8所示。考虑到本文所研究的翼型为对称翼型，其CL-α 曲线关于原点对称，CD-α曲线关于y轴对称，因此仅在图8 中给出了α＞0 时的曲线变化情况[21]。由式(13)和式(14)可知：切向力与升力系数CL、阻力系数CD和攻角α有关，为使变桨后风轮出力效果得到进一步提升，以获取最大切向力系数为目标，确定理论最佳攻角。由图8 可知：当α = 19°时，CT达到最大值，即FT达到最大值，此时垂直轴风力机的风能利用率Cp也取到最大值，那么α = 19°可以看作垂直轴风力机叶片位于上风区的理论最佳攻角。同理，α = -19°即为下风区的理论最佳攻角。

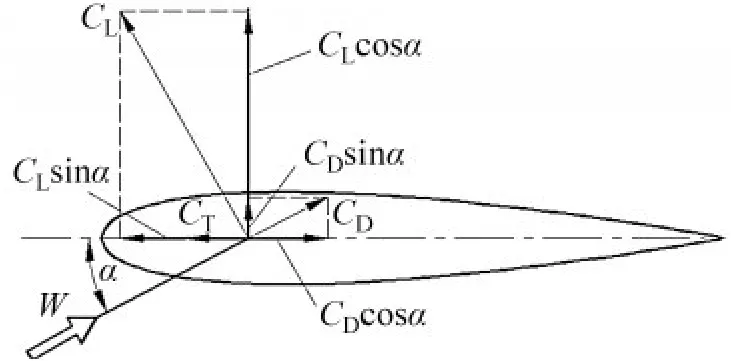
图7 叶片翼型气动力系数Fig.7 Aerodynamic coefficient of blade airfoil

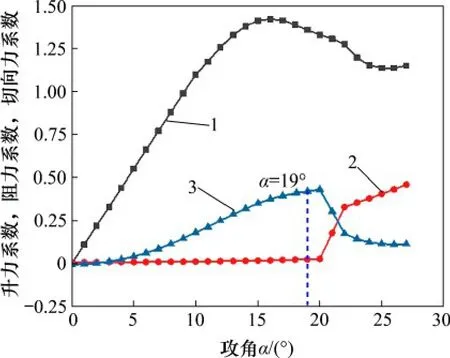
图8 升力系数、阻力系数和切向力系数随攻角α的变化Fig.8 Change of lift coefficient,drag coefficient and tangential force coefficient with attack angle

垂直轴风力机正常运行时，叶片攻角随方位角的改变呈类正弦规律变化[22]，不能一直保持在理论最佳攻角处，导致叶片所受气动载荷变化幅度较大，因此，需要对桨距角进行调节，使其尽可能地维持在理论最佳攻角处，以使得叶片所受气动载荷波动较小。为使计算结果更准确，采用DMST对叶片桨距角的调节规律进行分析[21]。

3.2 叶片桨矩角调节规律的计算

上述主轴合成力的计算是以桨距角β = 0°为基础的，而风力机在正常旋转过程中叶片攻角随其方位角不断变化，不能保证风力机叶片旋转过程中始终保持在理论最佳攻角。为降低叶片所受气动载荷和主轴合成力波动幅度，通过调节叶片桨矩角以使叶片攻角维持在最佳攻角。以叶片位于上风区为例，由式(1)可知，桨距角的表达式为

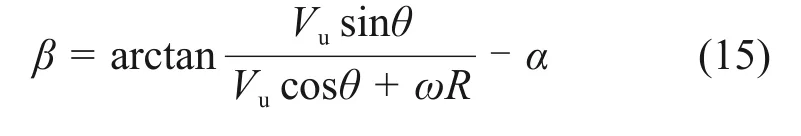
式(15)中，在上风区令叶片攻角α=19°，利用DMST计算出各个方位角下桨矩角，就能得到上风区桨距角的调节规律。同理，当叶片位于下风区时，令叶片攻角α=-19°，代入下风区诱导速度Va，可得到下风区桨矩角调节规律。上下风区的桨矩角调节规律如图9所示。

图9 叶片桨距角调节规律Fig.9 Adjusting rule of pitch angle

鉴于θ=0°和θ=180°时，叶片受到的升力平行于风轮支撑杆，不能有效推动风轮旋转，且叶片桨距角在θ=0°时由正值突变为负值，在θ=180°时由负值突变为正值，在实际工作条件下，难以实现这种调整。因此，在θ=0°和θ=180°时，将β调整为0°，此时攻角为0°，叶片受到的阻力最小[22]。基于上述修正方法，修正前后桨矩角调节规律对比如图10 所示。以上风区为例，在某一方位角下叶片桨矩角计算流程图如图11所示。

图10 叶片桨距角调节规律对比Fig.10 Comparison of adjusting rule of pitch angle

4 结果与讨论

为验证本文提出的变桨规律的有效性，基于1.1 节的1.5 MW 垂直轴风力机模型参数，利用DMST对叶片桨距角调节后风轮的主轴合成力和单叶片的切向力进行计算，并与变桨前相关数据进行对比。

4.1 变桨前后主轴合成力对比

利用DMST 计算变桨距前后主轴合成力变化趋势对比如图12所示。由图12可知：叶片桨距角调节前后，主轴合成力都呈现周期性变化，且周期均为120°。变桨后，主轴合成力1个周期内总体变化趋势为先增大后减小再增大，而变桨前，合成力则是先增大再减小，变化趋势的改变说明变桨可在一定程度上改变合成力波动情况。

综上所述，根据IDC转移程度不同，miR-200c mRNA可能出现不同程度的升高，其表达水平可能受到EZH2的调控，下调EZH2表达可引起乳腺癌细胞侵袭转移能力的增加。因本研究样本原因，虽然miR-200c、EZH2的表达改变对于乳腺癌的侵袭转移具有重要的意义，但是EZH2外源性调控的临床应用还需要更多的基础和临床证据。

以1个周期为例分析可知，变桨前后合成力均在方位角为6°左右时达到最低值。当方位角处于54°＜θ ＜78°时，变桨前主轴合成力达到最大值，而变桨后合成力则较变桨前大大降低。尤其当方位角处于24°＜θ ＜102°时，发现变桨后合成力变化趋势较平缓，最大差值约为22 kN，而变桨前合成力变化趋势较剧烈，最大差值约为41 kN，合成力振荡幅度总体降低了19 kN左右。

由于变桨前后主轴合成力的平均值有所变化，为评价该主轴合成力变化幅度，引入变异系数表示合成力波动和主轴振荡幅度：

式中：S 和M 分别为主轴合成力的标准差和平均值。

经过计算可知，调节桨矩角后，变异系数由0.118 降为0.109，降低了约8.26%，即这种变桨矩规律在理论上能有效减小合成力的振荡幅度，降低单向剪切来流风下合成力造成的主轴偏移和震颤等影响，进而提高风力机的使用寿命。

4.2 变桨前后切向力对比

利用DMST 计算变桨前后单叶片周向切向力如图13 所示。由图13 可知：叶片桨距角调节后，方位角为60°＜θ ＜150°和228°＜θ ＜288°时，切向力较变桨前有显著提高，而在其余方位角下，切向力虽然小于或接近变桨前的切向力，但切向力差值较小。结果显示，单个叶片的平均切向力由变桨前的16.2 kN 增长到17.5 kN，提高约8.02%。这表明该变桨规律能够有效提升叶片的切向力，进而提升风力机的气动性能。

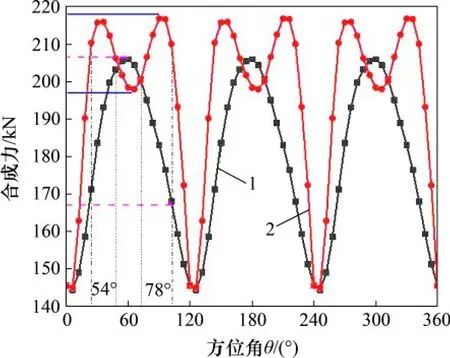
图12 主轴合成力对比Fig.12 Comparison of synthetic force of main shaft

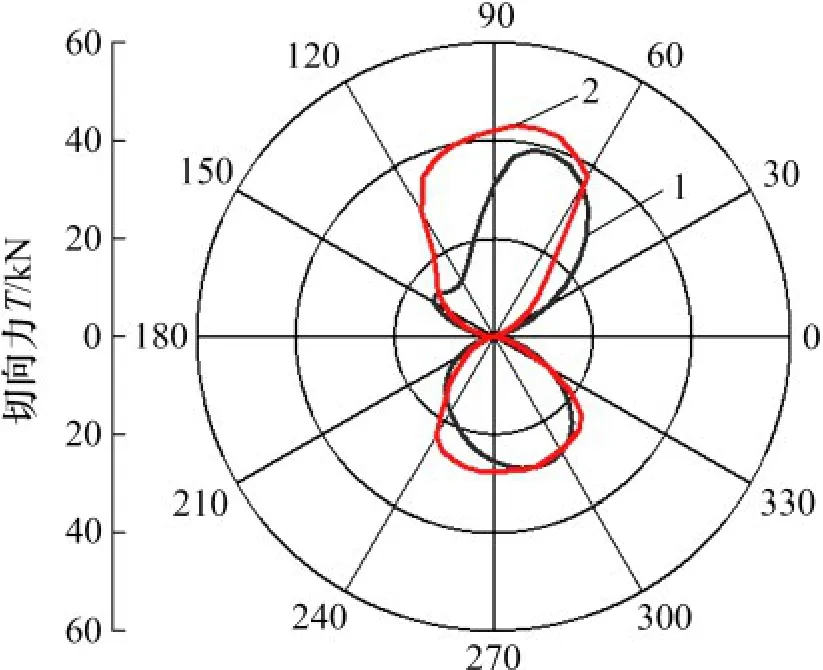
图13 单叶片周向切向力变化值Fig.13 Change value of circumferential tangential force of a single blade

5 结论

1)针对1.5 MW H型垂直轴风力机，阐述了主轴偏振效应的产生机理。风轮旋转1周过程中，叶片攻角变化范围大，气动载荷差异较大是形成主轴偏振效应的重要原因。利用DMST 计算了风剪效应下叶片载荷作用到主轴上的合成力，其合成力随风轮旋转呈周期性变化且最大极差值为62 kN左右。

2)以最大叶片切向力系数为研究目标，得到了大型H 型垂直轴风力机在上、下风区的理论最佳攻角分别为19°和-19°，并依据DMST制定了合理的桨矩角调节规律。

3)衡量主轴合成力振荡幅度的变异系数降低了约8.26%；单个叶片的平均切向力提高了约8.02%。这说明利用变桨技术不仅可以有效提高风轮整体的出力效果，而且能有效降低主轴合成力的振荡幅度，为大型H 型垂直轴风力机的可靠性运行和规模化应用提供了理论依据。