四自由度绳驱动刚柔混合式波浪运动补偿机构的动力学建模

姜媛，唐梁，陈原

(山东大学(威海)机电与信息工程学院，山东威海，264209)

船用吊装设备是实现货物在船与船之间、船与陆地之间进行交换的媒介。运用于港口码头的船用吊装技术影响货物的装卸效率，决定货物的交换质量与效率，尤其是海军的后勤远洋补给，军舰的装备补给效率可能影响一场局部战争的成败，因此，发展高技术水平的船用吊装设备，提高船用吊装技术，对未来的远洋补给和作战具有重大的意义。通常，受波浪的影响，船舶会产生横移、纵移、升沉、横摇、纵摇、艏摇6个方向的运动，使得被补给船与补给船之间产生6个方向上的相对运动。船舶之间的相对运动会影响到货物吊装的质量，例如，波浪运动造成被补给船和补给船之间发生的升沉相对运动会导致放下的货物与甲板发生碰撞，或者使货物再次发生悬空；波浪运动产生船舶之间的横摇相对运动会造成货物下放的位置发生偏转，使其易于与邻近货物发生碰撞。为了保证甲板上工作人员和货物的安全，应减小甚至避免货物与甲板或者货物之间碰撞的发生，因此，亟需研制波浪运动补偿技术，减少波浪运动对吊装作业的影响。

现有的波浪运动补偿技术大都只对升沉方向的相对运动进行补偿，分为被动式和主动式。主动式补偿系统通过对母体状态信号的反馈来控制补偿执行器，抗干扰能力强，精度高，补偿效果佳，主要有液压伸缩补偿、拖缆绞车收放补偿、吊臂变幅式补偿等系统类型[1-3]。被动式补偿系统多见于升沉方向补偿，较为典型的是随动车补偿[4-5]，这种补偿系统无需主动控制、提供能源，但补偿精度低、性能差。转运过程中精度与转运物安全息息相关，随着世界贸易发展和我国军事不断进步，单一升沉或摇摆方向的运动补偿已经不能满足各方需求。为了保证补给的安全性，提高补给效率，国内外对多维方向的波浪运动补偿技术进行了研究，它们主要通过绳索驱动的柔性冗余并联机构或者刚性并联机构来实现多维方向的波浪运动补偿技术。例如，美国海军研究办公室研制了六自由度并联波浪运动补偿装置LVI LO/LO，它使用惯性测量单元和摄像机阵列来检测舰船之间的相对运动，并通过8根绳索对动平台实现冗余控制[6]。胡永攀等[7-8]提出了一种绳驱动六自由度并联式波浪运动补偿装置，研究了该装置的鲁棒控制方法，并进行了抗摆性能分析，但是，这2种六自由度并联式波浪运动补偿装置都是纯绳索驱动冗余并联机构，而绳索只受拉力不受压力，当机构动平台的运动需要绳索伸长时，可能达不到预期的运动参数。邱广庭等[9-10]提出了一种三自由度刚性并联式波浪运动补偿装置，该装置能克服波浪运动对起重机相对运动的影响。LU 等[11]提出了一种3UPU/PU 刚性并联平台，用于船舶甲板的自动补偿，但是，这2种刚性并联机构都只具有3个方向上的相对运动补偿，在复杂的海况下不能有效地保证货物转运的安全。KIM等[12]研制了一种六自由度波浪运动补偿装置，它利用机器视觉来检测货物与船舶之间的相对运动，并通过智能平台来实现波浪运动补偿，但是，该机构结构复杂，实用性差。郭霆等[13]提出了一种复合式6-SPS波浪补偿稳定平台，但是，该机构采用双层结构，所占空间大，控制灵巧性不足。刚性并联机构能很好地实现动平台的多维方向运动，可以满足波浪运动补偿过程中对多维方向运动补偿的需要，但是，刚性并联机构受制于驱动和关节运动范围的限制，其工作空间较小，且机构质量较大，不适宜应用于运动范围较大的波浪运动补偿机构。近年来，绳牵引并联机构因具有质量小、驱动绳索的长度不受限制、较大的工作空间、自身惯量小等优点而被广泛关注[14]。然而，绳索只受拉力不受压力，绳索在伸长过程中可能会得不到预期的速度或加速度，从而影响动平台的控制效果，甚至引发安全事故。为此，一些国内外学者在绳牵引并联机构的构型基础上，引入刚性约束支链，构成绳驱动刚柔混合式机构。刚柔混合式结构既具有纯绳驱动并联机构的工作空间大、动态特性好等优点，同时，引入的刚性支链增强了该机构的整体刚度，又弥补了绳索只受拉力不受压力的缺点，使得该机构的控制更加完善。对绳驱动刚柔混合式机构的研究主要有：尚波[15]提出了一种由3根绳索与1个刚性S支链组成的两自由度的新型刚柔结构，将其应用于仿生关节；郭浩[16]提出了一种多连杆绳驱动机器人，该结构的基本单元由4根驱动电缆和1 个被动的S 刚性支链组成；KOSSOWSKi等[17]研制了一种柔索驱动桁架，该装置用6根控制电缆进行驱动，其中用1个由18个旋转关节组成的被动支链来维持结构的稳定性，使结构具有3个平移与1个旋转四自由度；MAO等[18]研制了一种康复训练机器人，用7根绳索构建了一个两层的并联结构，其中间支链由若干关节副串联组成被动支链，实现该机器人模仿人手臂的5个自由度方向的运动；谢少荣等[19]提出了一种混合驱动柔索并联仿生眼结构，该结构由3根绳索与1个R-S 主动支链来实现眼部结构的三维转动；BEHZADIPOUR 等[20]提出了一种基于电缆牵引的并联机器人，由3对绳索和1个主动UPU刚性支链构成，该结构只具有3个方向上的平移运动。对于刚柔混合式驱动并联机构，其中间支链的结构类型影响其整体结构的自由度，也因此使得刚柔混合式并联机构广泛应用于少自由度的需求场合。现有的研究其刚性支链大多是一个被动的支链，支链本身不具有驱动，只起约束作用。在一些实际应用当中，刚性支链由若干运动副串联而成，结构比较复杂。本文作者提出一种新型四自由度刚柔混合式结构，将其应用于波浪运动补偿机构。该机构以绳牵引结构为框架，继承了绳牵引结构的轻盈性、灵活性，保留了大部分工作空间；其刚性支链由PS 副串联连接，支链结构简单，增强了结构的整体刚度，同时，该支链还提供直线驱动，弥补了绳索受拉力不受压力的不足，使得动平台的运动控制更加完善。

1 绳驱动刚柔混合式波浪运动补偿机构的创新设计

补偿原理图如图1 所示。在货物的补给过程中，受波浪的影响，船与船之间发生的6个方向上的相对运动会使得补给货物与被补给船的甲板之间发生碰撞，引发安全事故，特别是升沉方向、横摇、纵摇和艏摇等4个方向上的相对运动会比其他2 个方向的相对运动带来更加严重的碰撞，因此，本文将创新设计一种补偿来自这4 个方向(升沉、艏摇、横摇、纵摇)的相对运动的四自由度波浪运动补偿机构。

在绳牵引并联机构中，假设其动平台具有p个自由度，绳索驱动数目为q。为了实现对机构的完全约束定位，绳索张力需要形成封闭矢量，即当绳索驱动数目q=p+1时，绳牵引并联机构才能够抵抗作用在动平台上的外力旋量。对于刚柔混合式并联机构，要实现机构的完全定位约束，若其刚性支链作为被动支链，不提供驱动，则其所需要的绳索驱动数目为q=p+1；若其刚性支链作为主动支链，提供驱动，则其所需要的绳索驱动数目为q=(p-1)+1。故要实现4 个方向的相对运动补偿，该波浪运动补偿机构需要由4根绳索以及1个刚性的PS 主动支链组成。基于此思想，本文设计了如图2(a)所示的四自由度刚柔混合式波浪运动补偿机构。该机构的绳索支链由伺服电机带动绞线盘来控制绳索的伸缩，通过导线盘和动平台上的铰点将上平台和下平台连接在一起；其刚性支链由直线电机控制其移动副的伸缩，该支链的上端与上平台几何中心固连在一起，下端通过1个球副与下平台几何中心连接在一起。通过对绳索以及刚性支链运动参数的控制，实现对动平台位置及姿态的控制。

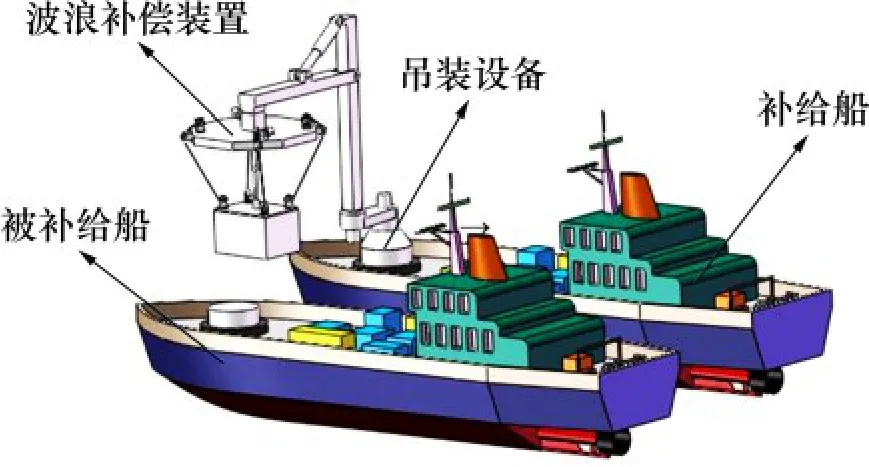
图1 补偿原理图Fig.1 Compensation principle

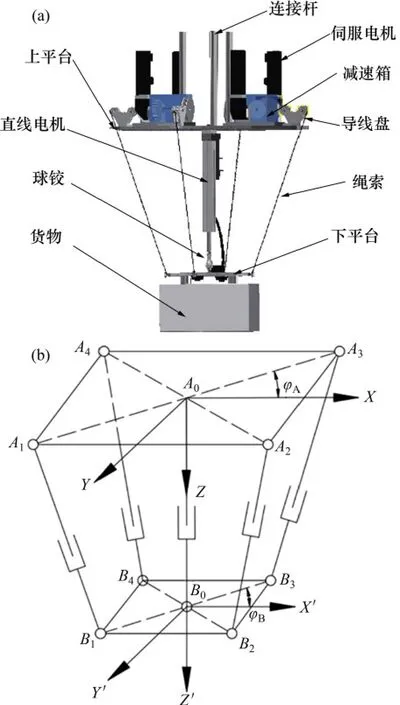
图2 四自由度绳驱动刚柔混合式波浪运动补偿机构Fig.2 Four-degree-of-freedom rope driven rigid-flexible hybrid wave compensation mechanism

将该四自由度绳驱动刚柔混合式波浪运动补偿机构安装在补给船的吊装设备上。补给船对目标船只进行货物补给，在货物吊装交接的过程中，由波浪产生的相对运动会使货物不能平稳地放在目标船只的甲板上。此时，可以通过对该波浪运动补偿机构中绳索以及刚性支链运动参数的控制，使货物在下放过程中始终与目标船只保持姿态一致，并且在升沉方向上的相对运动速度尽可能小，使货物释放后不会再次悬空，也不会对甲板产生较大的冲击，这样就有效地保障了货物补给的安全性。

该四自由度刚柔混合式波浪运动补偿机构的结构简图如图2(b)所示，绳索支链AiBi(i=1，2，3，4)等效为SPS(S表示球副，P表示移动副)支链，刚性支链AiBi为PS 支链。采用螺旋理论对该机构进行自由度验证[21]。螺旋的相逆性与坐标系的选择无关，对支链分别建立不同的分支坐标系，对于绳索支链AiBi(i=1，2，3，4)，以Ai点球副为原点，建立如图3所示的支链坐标系O-XYZ。

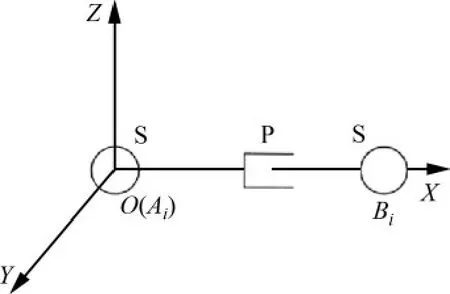
图3 绳索支链AiBi的坐标系Fig.3 Coordinate system of rope branch AiBi

在绳索支链AiBi坐标系下的运动螺旋系SAiBi为

式中：li为绳索支链AiBi(i=1，2，3，4)的长度。

经计算，该螺旋系的秩rank(SAiBi)=6，不存在反螺旋系，4条绳索支链AiBi都属于六自由度分支。同理，以Ai球副的中心为原点，建立了如图4所示的PS刚性支链A0B0的O-XYZ支链坐标系。

PS 刚性支链在刚性支链坐标下的螺旋系SA0B0为

图4 PS刚性支链坐标系Fig.4 Coordinate system of rigid branch PS

求得该螺旋系的反螺旋系为

该支链被约束了2个自由度，即沿X轴方向的移动和沿Y轴方向的移动，因此，该波浪运动补偿机构具有3个转动1个移动四自由度(绕X，Y，Z的转动以及沿Z轴的移动)。对于由1个少自由度的串联分支和若干个6自由度分支构成的第1类非对称并联机构，其自由度完全决定于其少自由度串联支链，因此，该补偿机构满足结构设计要求。

2 绳驱动刚柔混合式波浪运动补偿机构的运动学建模

2.1 机构的位置反解

机构位置反解是在已知动平台在空间的位置和姿态条件下，求解绳子以及刚性移动副的伸缩位移，即已知动平台的位姿(ZB0，α，β，γ)，求各驱动支链的长度L(l0，l1，l2，l3，l4)。

在机构的静平台(上平台A)建立固定坐标系A0-XYZ，以静平台的几何中心A0为原点，X 轴、Y轴、Z轴的方向如图2(b)所示。在机构的动平台(下平台B)建立动坐标系B0-X′Y′Z′，以动平台的几何中心B0为原点，X′轴、Y′轴、Z′轴的初始方向分别平行于固定坐标系的X轴、Y轴、Z轴。

在静平台A 中，各铰点在固定坐标系A0-XYZ中的坐标为Ai(AixAiyAiz)，各铰点相对于固定坐标系原点A0的矢径用rAi表示。动平台各铰点Bi在动坐标系B0-X′ Y′ Z′中的坐标表示为B′i(B′ixB′iyB′iz)，各铰点相对于动坐标系原点B0的矢径用rB'i表示，各铰点相对于固定坐标系原点A0的矢径用rBi表示。用X-Y-Z 型欧拉角描述动平台相对于静平台的运动，则动平台相对于静平台的位姿就可以用3个角度α，β和γ描述，动坐标系相对于固定坐标系的姿态变换矩阵为

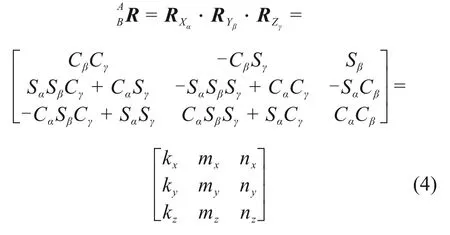
通过坐标变换转换到固定坐标系中，相对于原点B0的矢径rB'i动平台中的任一铰点在固定坐标系中的矢径rBi为

则驱动绳以及刚性支链的位移矢量Li(i =0,1,…,4)在固定坐标系中表示为

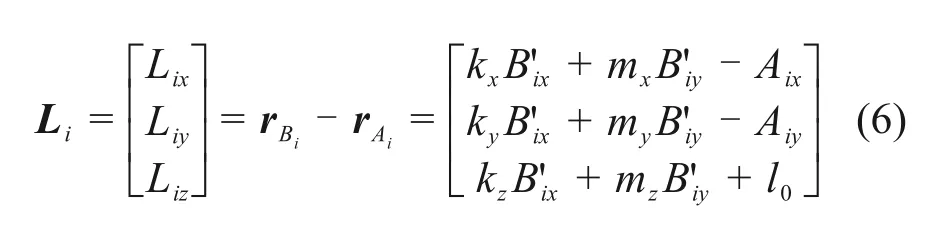
各支链长度li的方程可以表示为

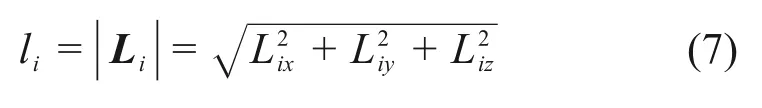
式(7)即为绳驱动刚柔混合式波浪运动补偿机构的位置反解。根据具体的机构尺寸以及动平台的位置和姿态(ZB0，α，β，γ)，可求出各个驱动的位移L(l0，l1，l2，l3，l4)。表1 所示为动平台的3 组反解算例。

2.2 机构的位置正解

求机构的位置正解，即在已知绳子以及刚性移动副的伸缩位移条件下，求动平台在空间的位置和姿态，即已知各驱动的长度L(l0，l1，l2，l3，l4)，求动平台的位姿(ZB0，α，β，γ)。

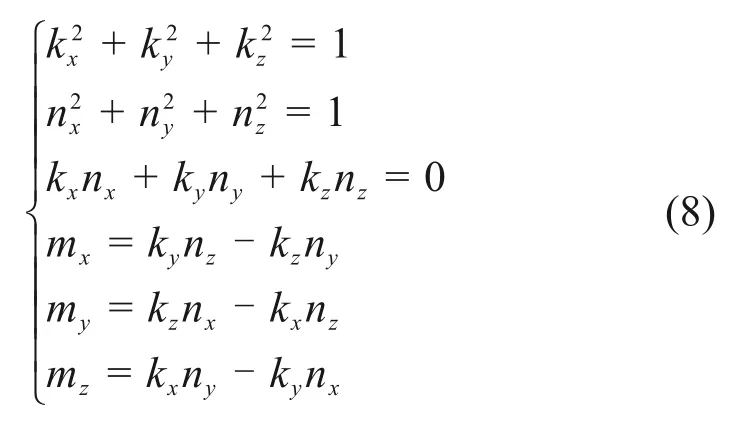
同时，由方程的位置反解可以得到

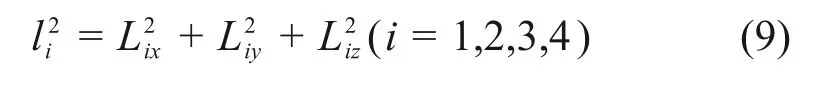
联立方程组(8)以及式(9)，运用数值迭代法可以求得旋转矩阵中9个元素的解。然后，由旋转变换矩阵(4)可以得到α，β，γ的表达式：

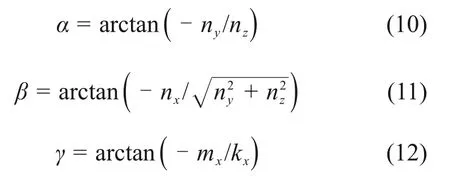
又由机构的结构可知：

当已知各驱动的长度L(l0，l1，l2，l3，l4)时，可求得该动平台的位姿(ZB0，α，β，γ)，即求得该动平台位置正解。将表1 中得到的位移作为输入，得到如表2所示的动平台的输出位姿，将输出位姿与给定位姿进行对比得到位姿误差。由表2 可知：位姿误差较小，皆在10-5的数量级内，说明了本文所提出的位置正解与位置反解模型的正确性。

2.3 机构的速度分析

对位置反解式(7)两端分别对时间求导，可得第i根驱动绳的速度l˙i：

式中：ei=Li/li，为沿Li方向的单位向量；vBi为动平台各铰点Bi的速度，

vB0=[vx，vy，vz]T，为动平台中心点B0的线速度；ωB=[ωx，ωy，ωz]T，为动平台的角速度。

将式(15)代入式(14)得

对于全部5根驱动绳，有：

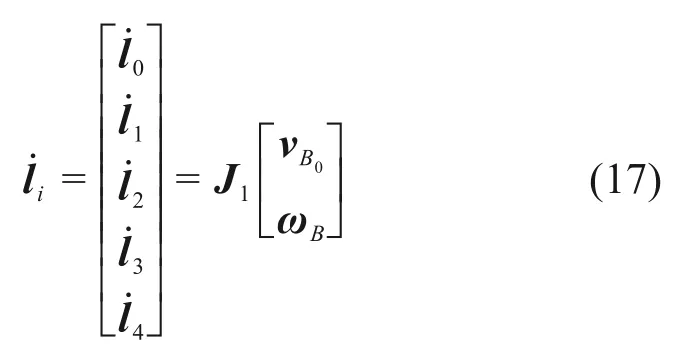
表1 动平台的位置反解算例Table 1 Counter-solution example of moving platform

表2 动平台的位置正解算例Table 2 Positive position solution example of moving platform

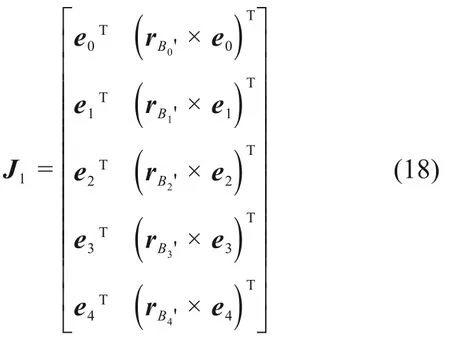
式中：J1为驱动速度与动平台六维速度间的映射矩阵。

用X-Y-Z欧拉角(α，β，γ)表示动平台的姿态，将欧拉角对时间的导数α˙，β˙和γ˙转换到定坐标系中，则动平台的角速度用欧拉角的导数可以表示为

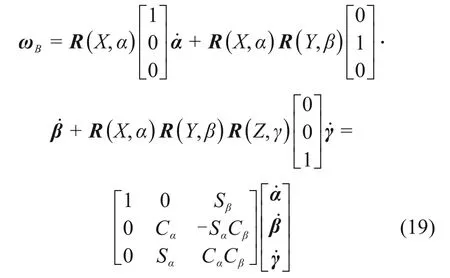
式中：R( X,α )，R( Y,β )和R( Z,γ )分别为绕X，Y，

Z轴旋转α，β和γ角的旋转矩阵。动平台的速度可用线速度和角速度表示为

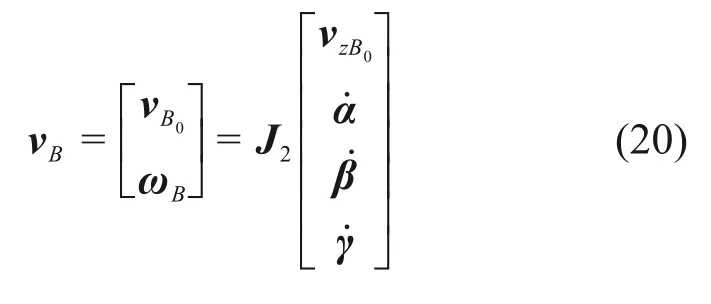
其中：

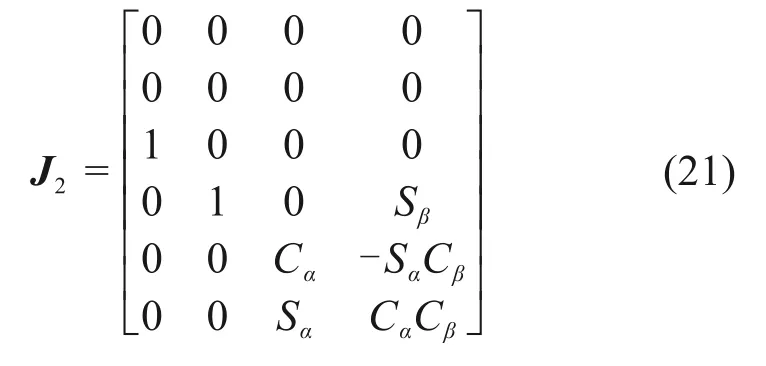
将式(20)代入到式(17)得：

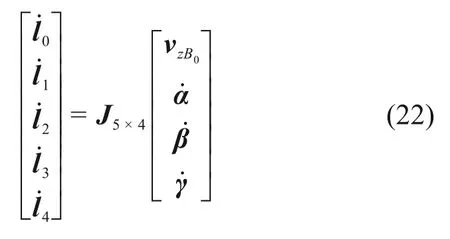
式中：J5×4=J1*J2∈R5×4表示该机构的雅克比矩阵。

2.4 机构的加速度分析

设ɑ=[ɑxɑyɑz]T和ε=[εxεyεz]T分别表示动平台的线加速度和角加速度，ɑli表示沿Li(i=0，1，…，4)方向上的加速度。对式(16)两端对时间分别求导得

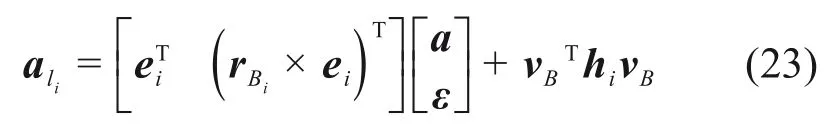
将式(20)两端分别对时间t求导得

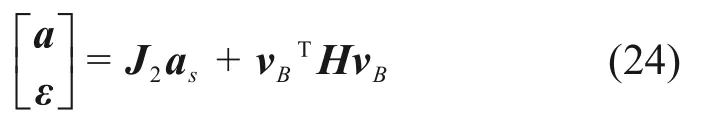
3 绳驱动刚柔混合式波浪运动补偿机构的动力学建模

3.1 动平台的动力学模型

动平台的受力如图5 所示。图5 中，m 为动平台的质量；Fe为加载在动平台上的外力；Me为加载在动平台上的外力矩，I为运动平台在中心点的惯性张量，vB0和ωB分别为动平台中心点的速度和角速度。

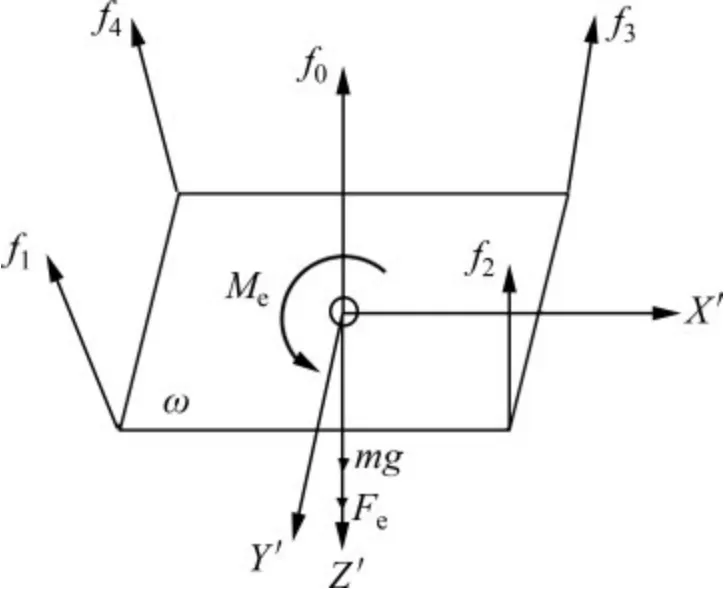
图5 动平台的受力模型Fig.5 Force model of moving platform

动平台的动力学模型由平台的移动和转动这2部分组成，因此，动平台的动力学模型可以表达成如下式子：

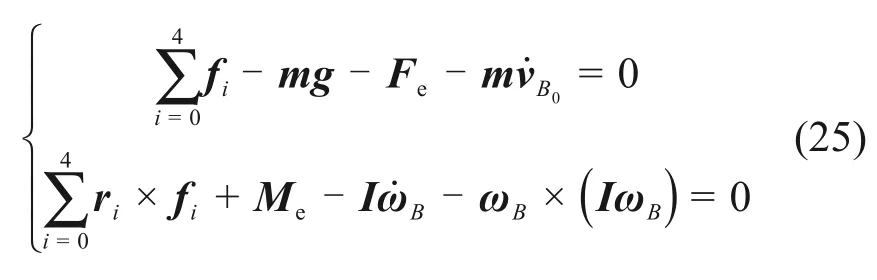
将式(25)改写成矩阵形式：

式中：D =

3.2 绳索驱动器的动力学模型

绳索驱动器的受力模型如图6 所示。图6 中，Jr为驱动单元的等效转动惯量；φi为第i 个电机的转角矢量，以绳索长度的增加方向为正方向，当动平台在初始位置时，设定φi=0；Cr为绳索驱动单元的等效阻尼系数矩阵；R为绳索驱动器的等效半径；fi为第i 根绳索的拉力；Ma为驱动器的转矩。由牛顿第二定律可以建立如下动力学模型：

可以将式(27)改写为如下矩阵形式：

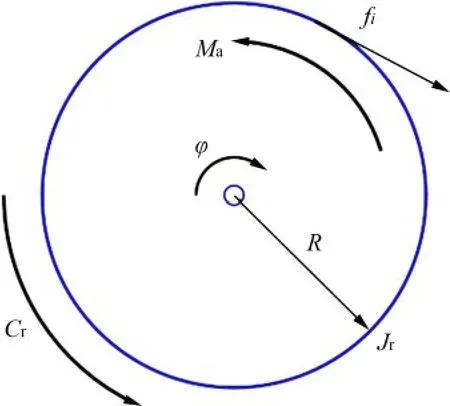
图6 绳索驱动器的受力模型Fig.6 Force model of rope drive

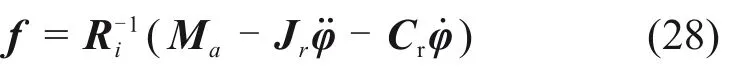
式中：f=[f1f2f3f4]T；Ri=diag[R1R2R3R4]；Ma=[Ma1Ma2Ma3Ma4]T；Jr=diag[Jr1Jr2Jr3Jr4]；φ=[φ1φ2φ3φ4]T；Cr=diag[Cr1Cr2Cr3Cr4]。

3.3 驱动刚柔混合式波浪运动补偿机构的动力学模型

联立动平台的动力学模型与驱动器的动力学模型，可以建立驱动刚柔混合式波浪运动补偿机构的动力学模型。由几何关系可得第i根绳索的变化量Δli与第i个电机的转角矢量φi存在以下关系：

对式(29)两边同时对时间求导，可以求得如下转角矢量φ的速度和加速度：

将式(30)代入绳驱动器动力学方程(28)，可以得出绳驱动器动力学方程：

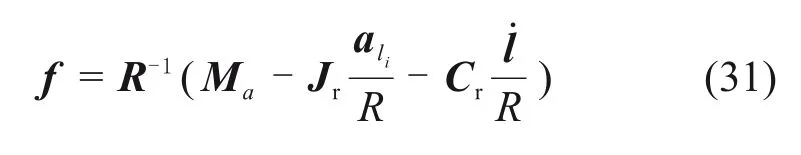
联立驱动器的动力学方程(31)和动平台的动力学方程(26)，可以求得驱动刚柔混合式波浪运动补偿机构的动力学方程：

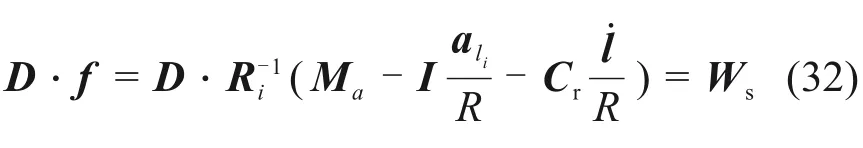
4 数值仿真算例

定义波浪运动补偿装置的结构参数如下：静平台的长为320.00 mm，宽为554.26 mm；动平台的长为316.5 mm，宽为125.0 mm；动平台初始位置为水平，其中心点的初始位置为[0,0,-367.14]；绳索驱动器的等效半径R=50 mm。不考虑绳索的质量以及绳索与滑轮之间的摩擦力。

4.1 运动学模型的数值仿真

建立该波浪运动补偿装置的Adams 模型，对该模型进行运动学仿真，得到如图8所示各驱动的运动学参数。图8(a)中，各驱动的长度变化平滑，与图7(a)中的驱动长度变化相一致。图8(b)中，各驱动的速度变化较为平滑，在大部分时间内与图7(b)所示变化趋势保持一致，在1.5 s 左右处出现跳动， 最大误差为5.327 mm/s， 平均误差为2.141 mm/s，为理论计算值的1.4%，在可接受误差范围内。图8(c)中，各驱动的加速度变化在大部分时间与图7(c)所示变化趋势保持一致，在0.5 s 和1.5 s处出现小幅波动，波动的误差为±1.237 mm/s2，在可接受的范围内。

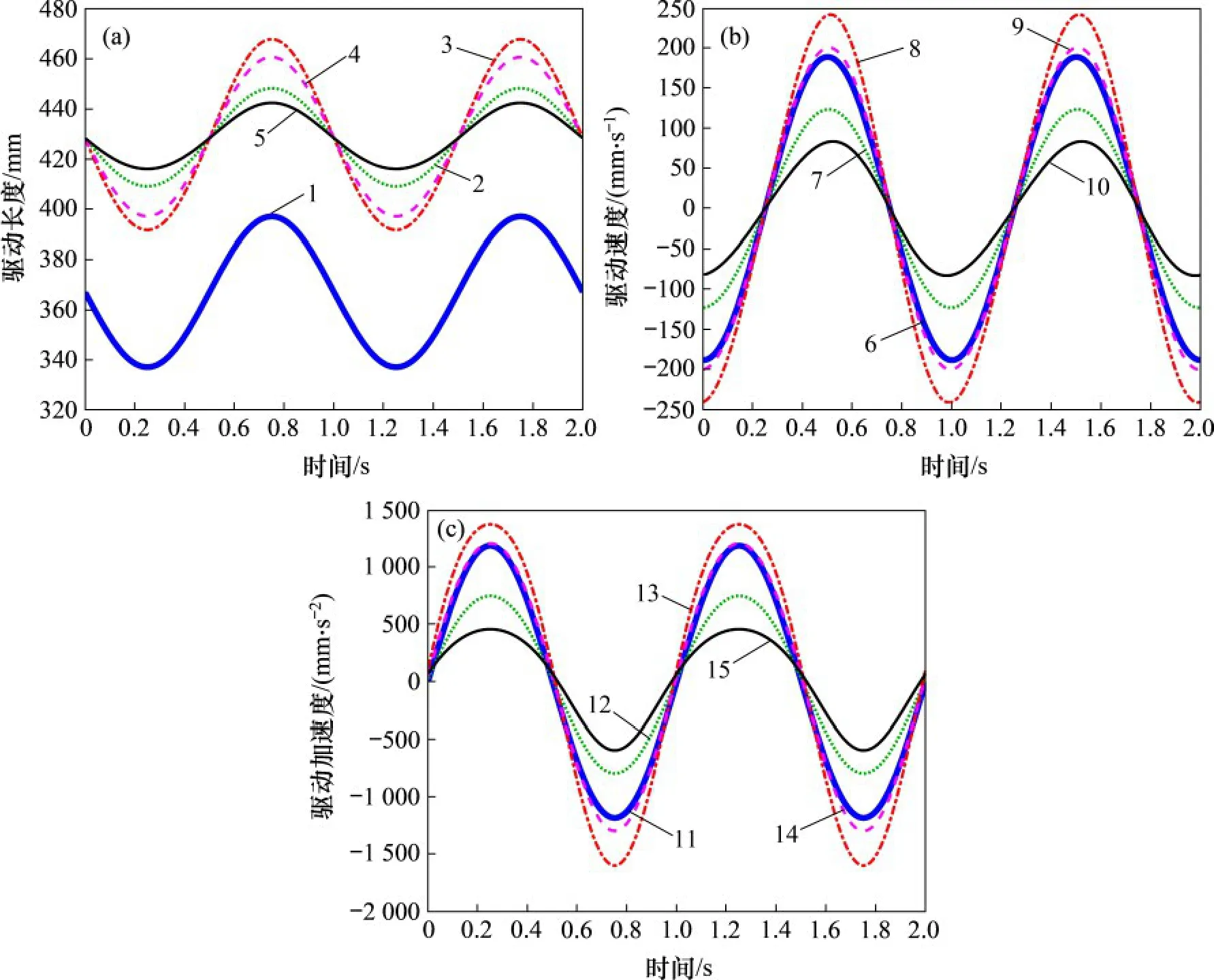
图7 运动学模型的数值仿真Fig.7 Numerical simulation of kinematics model

图8 虚拟样机的Adams运动学仿真Fig.8 Adams kinematics simulation of virtual prototype

通过将Adams 运动学仿真所得到的驱动运动学参数的结果与MATLAB 数值模拟所得到的结果进行对比发现：在所给周期内，其驱动的长度、速度以及加速度基本一致，误差在可接受范围以内，证明了本文所推导的位置反解、速度模型以及加速度模型是正确的。

4.2 动力学模型的数值仿真

根据所推导的动力学公式得到MATLAB 数值模拟结果，如图9 所示，将其与如图10 所示的Adams动力学仿真结果进行比较。

将虚拟样机的Adams 动力学仿真与动力学模型的数值仿真图进行分析发现：刚性支链与绳索的受力连续，不存在受力突变的位置，且绳索受力一直为正，处于张紧状态，说明了该结构具有良好的受力特性。将虚拟样机的Adams 动力学仿真与动力学模型的数值仿真图进行对比分析，发现无论是刚性支链还是绳索支链，其受力的大小以及变化趋势基本保持一致。进一步地，以刚性支链为例进行误差分析，得到如图11 所示的刚性支链受力对比图。由图11 可知：MATLAB 和Adams 拉力仿真结果及其变化趋势基本吻合，误差的最大值出现在1.37 s 左右，最大误差为0.43 N，为理论计算值的1.6%，在可接受的范围内。

图9 动力学模型的数值仿真Fig.9 Numerical simulation of dynamic model

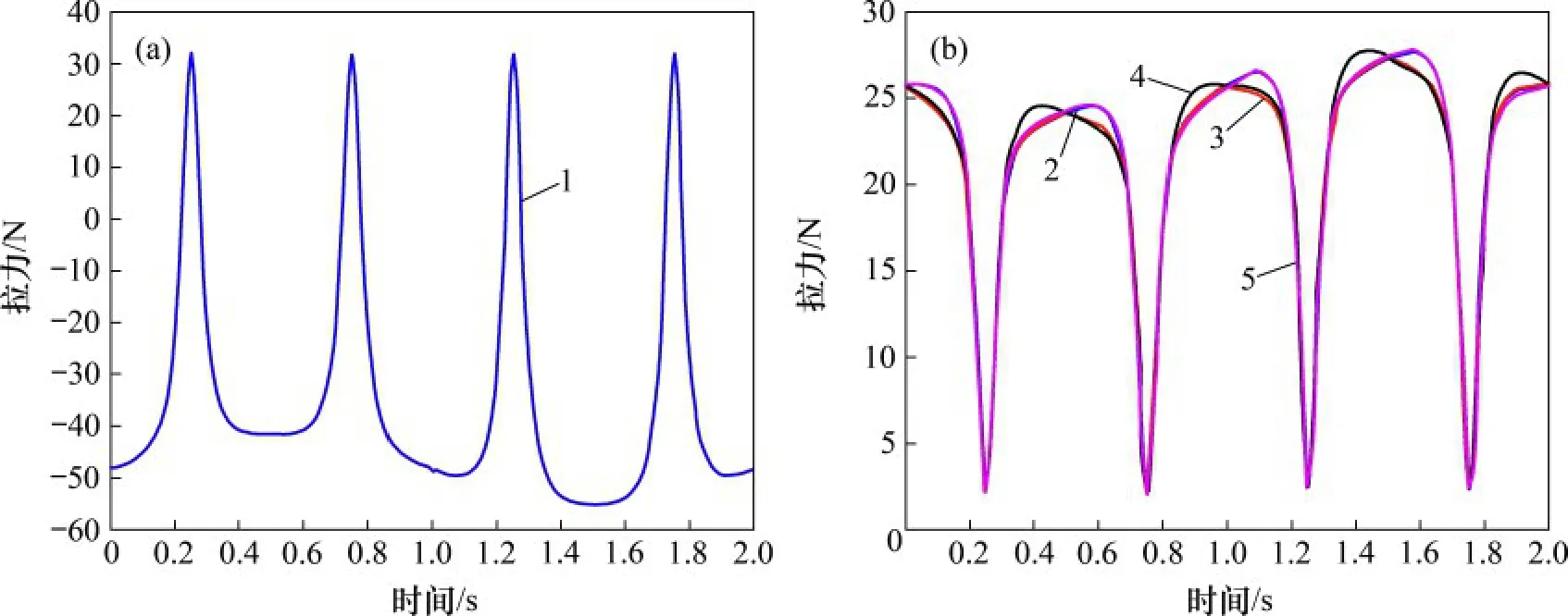
图10 虚拟样机的Adams动力学仿真Fig.10 Adams dynamics simulation of virtual prototype

图11 刚性支链受力对比图Fig.11 Comparison chart of rigid branch force

通过对比发现，绳索拉力的仿真曲线和理论计算曲线在所给周期内基本保持一致，误差在可接受范围内，可以忽略不计，验证了所推导的动力学的正确性。

5 试验

为验证模型动平台的姿态的动态特性，结合实际参情况优化参数，搭建了实验样机，如图12所示。

图12 实验样机Fig.12 experimental prototype

将船舶3个方向的摇摆运动用3组幅值与周期不同的旋转正弦函数表示，如表3所示。

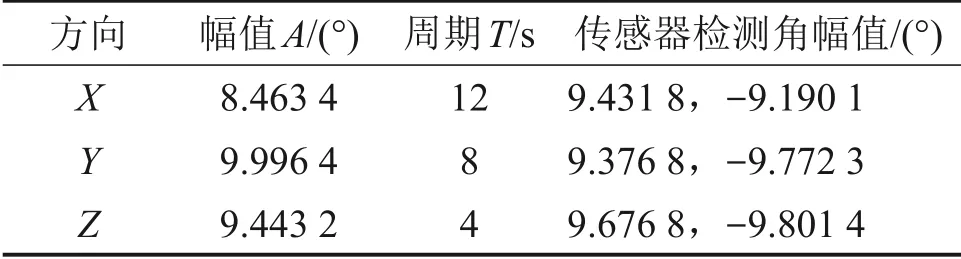
表3 旋转正弦函数Table 3 Rotate sine function

分别比较各轴传感器检测角幅值与目标正弦函数幅值，得到绝对值误差均为1°左右。对3组测量的旋转角数据与输入函数图像进行拟合，结果如图13所示。

从图13可以看出：X方向和Z方向幅值稍大于传感器检测幅值，而Y方向幅值稍小于传感器检测幅值，误差主要是由绳索的弹性变形和步进电机的控制精度不足引起。动平台偏转结构示意图如图14 所示。此机构中，绳索A 和B 的拉力相等，横截面变化可忽略不计，因此，变形的主要影响因素为绳长。横摇与艏摇过程中绳索A 的伸长量比绳索B的大，导致偏角增大；而纵摇时，支链A和B长度变化小，张紧力大，电机驱动受到的阻尼较大，导致绳索支链长度变短，导致偏角减小。陀螺仪受环境影响，也可能导致误差出现。

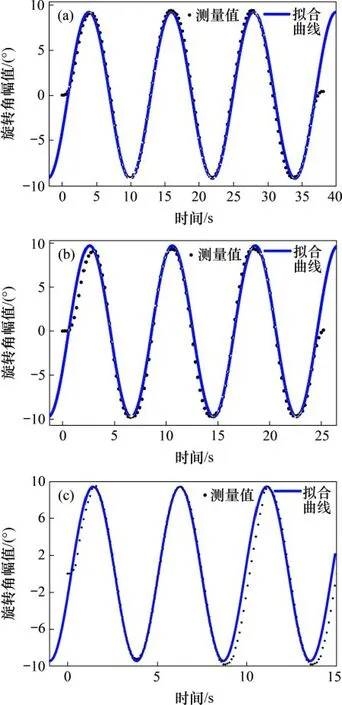
图13 摇摆幅度拟合曲线Fig.13 Fitting curves of swing amplitude

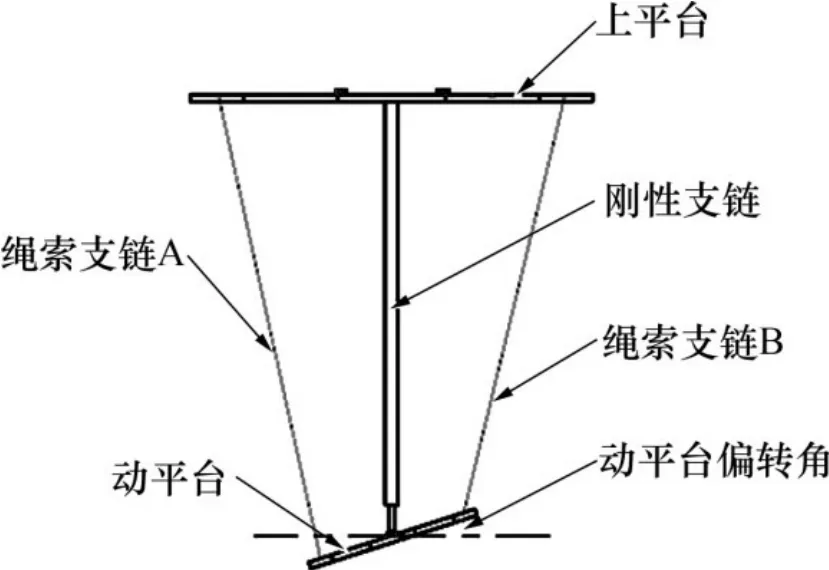
图14 动平台偏转结构示意图Fig.14 Schematic diagram of deflection structure of moving platform

6 结论

1)提出了一种用于四自由度绳驱动刚柔混合式波浪运动补偿机构，基于螺旋理论验证了其运动自由度，能满足波浪运动补偿的运动需求。

2)建立了该波浪运动补偿装置的位置正解与位置反解。利用数值迭代法对位置正/反解进行计算，位置误差都在10-5mm数量级，验证了位置正/反解模型的正确性。

3)推导了该波浪运动补偿装置的运动学模型，基于牛顿-欧拉法推导了该装置的动力学模型。运用仿真软件对所推导的数学模型进行验证，发现MATLAB 数值模拟结果与Adams 虚拟样机所得结果基本吻合，误差最大值为理论值的1.6%，在可接受范围内，验证了所推导的运动学与动力学模型的正确性。

4)通过实验检测了横摇、纵摇和艏摇的动态特性，输入幅值与测量幅值的误差较小，验证了机构运动学模型的正确性。