基于数字图像相关的旋转叶片全场测量

叶美图，梁晋，千勃兴，宗玉龙，龚春园

(西安交通大学机械工程学院机械制造系统工程国家重点实验室，陕西西安，710049)

旋转叶片的运动跟踪与变形测量是一个值得关注的问题[1-6]，在风力叶片[2-3]或直升机桨叶[4-5]等旋转机械寿命预测中，对大扭矩、高速运动下叶片材料性能的判断有重要意义。由于传感器在大型或高速旋转叶片上不好布置，而且传感器建立的观测点有限，不能对整个叶片任意位置的位移与变形进行测量，因此，接触式传感器难以满足旋转叶片的测量需求。在叶片表面粘贴标志点[3]，双目相机同时采集图像，通过立体视觉计算标志点的空间位置进而求得位移的方法，比接触式传感器便利，但不能实现全场位移测量[5-6]，从而无法获取应变场，因此，这种测量方式对叶片运动时表面的受力分析作用有限。数字图像相关已经被广泛使用于非接触式全场变形与应变测量[7-12]。经典的数字图像相关[8]使用牛顿法迭代求解变形系数，只包容子区小角度旋转。如RIZO-PATRON等[4]针对直升机旋翼桨叶仅旋转至特定位置进行图像采集与匹配计算进行了模态分析。叶片在宏观上绕轴旋转，测量旋转至任意位置处的变形时，通过相关函数直接匹配很可能找不到变形前后的相似子区，导致匹配失败。为此，一般使用较高的图像采集频率，并且要求相邻变形状态旋转角度较小，使每个状态都与其前一状态进行匹配。但是这种匹配方式会产生累计误差。

目前，已有学者使用数字图像相关法对旋转变形的全场测量进行了研究。ZHANG 等[9]考虑到圆周上像素的灰度之和不随旋转变化，选择具有十几层等距同心圆环作为匹配模板，每个圆环上的灰度均值作为向量的一个分量，在整像素搜索阶段，计算向量的相似性。匹配完成后，再结合曲面拟合法，能够得到变形前后比较准确的对应位置。WU 等[10-11]使用图像特征点匹配先求解出大致旋转角度，在对旋转子区进行整像素搜索完毕之后，通过2 步NR 亚像素迭代求解出目标节点准确的位置和子区的旋转角度。将这些参数向相邻节点传递作为迭代初值依次执行下去。ZHONG等[12]将笛卡尔坐标内的旋转转化为极坐标内的平移。将参考子区和变形子区的形状定义为1 个圆，用极坐标描述。再使用IC-GN迭代求解。

此外，直接使用数字相关进行旋转测量时，整像素位置和变形系数初值不容易确定，常见的解决方法就是使用特征点检测算法[13]或者直接贴标志点[14]求出参考图像和变形图像上的特征点对，假定物体的变形为仿射变形，使用RANSAC 算法求解出比较可靠的仿射变换参数[15]，然后，利用仿射变换的参数得到目标子区中心处整像素的位置以及形函数中的变形系数作为初值进行迭代计算[16]。在此基础上，本文结合双目视觉和数字图像相关法，提出一种更简便稳定的叶片旋转时的全场测量方法。将旋转前后的图像进行SURF检测，认为前后状态图像近似存在投影变换，利用RANSAC算法筛选出准确点对。使用特征点对求解前后状态的旋转参数(旋转中心和旋转角度)，对变形图像进行反向旋转变换，校正后的图像再与参考图像匹配。匹配得到对应节点后，再对这些节点正向旋转复原，得到原变形图像上的对应坐标。这样，可靠地解决了子区旋转角度过大难以匹配的问题。最后，通过立体视觉重建，得到特征表面的空间坐标，实现跟踪与变形测量的目的。

1 旋转问题的匹配策略

常见的叶片测量方式如图1所示，当被测对象较小时，采用相机观测整个对象；而当叶片较大时，可以结合频闪仪只观测1个叶片。

由于叶片旋转变形时，所有子区以近乎相同的角度和旋转中心进行旋转，而且旋转引起的位移远大于变形。因此，传统的数字图像相关法无法直接匹配大角度旋转的2个子区，在整像素和亚像素搜索阶段都会造成很大程度的不稳定。对于旋转前后的2 幅图像(参考图像和变形图像)，先基于SURF 检测得到2 幅图像上的1 组对应点，利用对应点求出旋转参数。根据旋转参数对变形图像进行反向旋转，然后进行子区匹配，可以避免大角度旋转和大位移造成的匹配失败，使散斑子区的追踪更稳定快速。匹配完成后，将校正图像上匹配得到的对应点正向旋转，得到它们在原变形图像上的坐标。利用高精度灰度插值函数，这种方法可以实现任意旋转角度下的子区匹配。

图1 旋转叶片的2种测量视角Fig.1 Two perspectives of rotating blade

双目旋转变形匹配方案如图2 所示，其中，θ1，…，θN为变形状态1～N 的旋转角度。在基准状态左图像上划定散斑计算区域，与右图像匹配重建三维点作为观测点的基准位置。然后，依次匹配每个变形状态和基准状态：1)根据2个状态计算的同名标志点对，求出2幅图像相对的旋转中心和角度，根据这2个参数将变形图像反向旋转(图2中路径a)。2)进行正常的相关匹配(图2中路径b)。3)将匹配得到的节点集合根据旋转参数再还原(图2中路径c)，从而左图像上的子区匹配完成，找到对应节点。4)在右图像上搜索左图像上的同名节点，匹配完成后进行三维重建得到观测点的变形位置(图2 中路径d)。因为三维测量实验中，相机光轴与被测面法线的夹角不大于15°，接近正视，所以，能够通过旋转前后的特征点对计算出较准确的旋转角度。

图2 双目旋转变形匹配方案Fig.2 Matching scheme of binocular rotation deformation

平面上绕旋转中心(s,t)旋转角度θ的坐标变换公式为

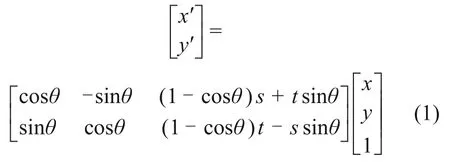
式中：(x′，y′)和(x，y)为旋转前后的图像坐标。

旋转叶片在转动时发生了刚体旋转和平移以及变形，可描述为仿射变换：

式中：m1，m2，m3和m4为旋转、拉压和剪切状态矩阵的元素；(tx,ty)为平移系数。对于参考图像和变形图像检测得到的n 对特征点坐标，代入式(2)可得

其中：m1= cosθ，m2= sinθ。旋转角度可根据m1和m2估计得出。

对照式(1)，可得

在(m1，m2，m3，m4)和(tx，ty)已知的条件下，求解式(5)，可得旋转中心为

通过式(1)对变形图像进行校正。根据反向映射的思路得到反向旋转后的图像[17]。匹配完成后，仍按照式(1)将匹配节点正向旋转复原。

2 数值模拟与精度评估

2.1 方法验证

使用高斯光斑模型[17-18]生成400 像素×400 像素的模拟散斑图像作为参考图像，施加正弦位移u =3sin(0.01πx)后再绕着图像中心旋转136°得到变形图像。使用本文方法进行匹配计算。

对参考图像和变形图像进行SURF检测后计算旋转参数。SURF检测计算大变形前后的旋转参数如图3 所示，其中，图3(a)所示为使用SURF 检测得到的参考图像和变形图像特征点的对应关系。共得到286 个特征点对，但是却存在误匹配点对。使用RANSAC 算法经过仿射变换的筛选后，剩下119个正确的亚像素特征匹配对。由计算的仿射变换参数可得夹角为136.42°。可见，变形较大时仍然能得出较准确的旋转角度。

实际中可能还存在其他因素导致旋转角度求解的误差可能偏大。假设检测得到的旋转角度为127°，对变形图像顺时针旋转127°后，与参考图像进行匹配。使用加入线性光强的SSD (sum of squared difference)函数表征2 个匹配子区相似性程度，使用双线性插值算法求解2个子区精确匹配时的图像灰度插值，使用一阶形函数表征运动和变形的模式[8]。子区半边长为15 像素，步长为12 像素，计算节点的规模为20×20，均布在整个图像上。各变形系数前后的迭代阈值设置为0.001，平均迭代3.7次收敛。匹配计算得到的位移场见图4。可见，子区在x方向位移场显示出正弦变形。

图3 SURF检测计算大变形前后的旋转参数Fig.3 Calculation of rotation parameters before and after large deformation by SURF detection

将匹配点逆时针旋转127°得到目标节点集。图5所示为旋转图像计算的位移场。由于变形引起的位移远小于旋转引起的位移，因此，x 和y 方向的位移场形状为近似平面。对这2个位移场的平方和求算术平方根，得到综合位移场(图5(c))，它显示出了节点集的旋转运动。

可见，本文提出的方法，能够正确得到匹配结果，对变形与大角度旋转问题具有普遍适用性。

2.2 精度评估

与传统的直接匹配方法相比，提出的方法对图像使用双三次插值进行了1次旋转校正。对原始散斑图旋转136°得到变形散斑图。通过所提出的方法计算得到位移场，其中图像反向旋转127°后匹配。设定的计算参数和节点与上节相同。将这些节点进行136°逆时针旋转得到的坐标作为真值，分析与所提出方法计算结果的偏差。图6所示为提出方法得到的位移场与理想位移场的偏差。x 和y方向的位移场分别与图5(a)和图5(b)所示的相似，不再绘制。

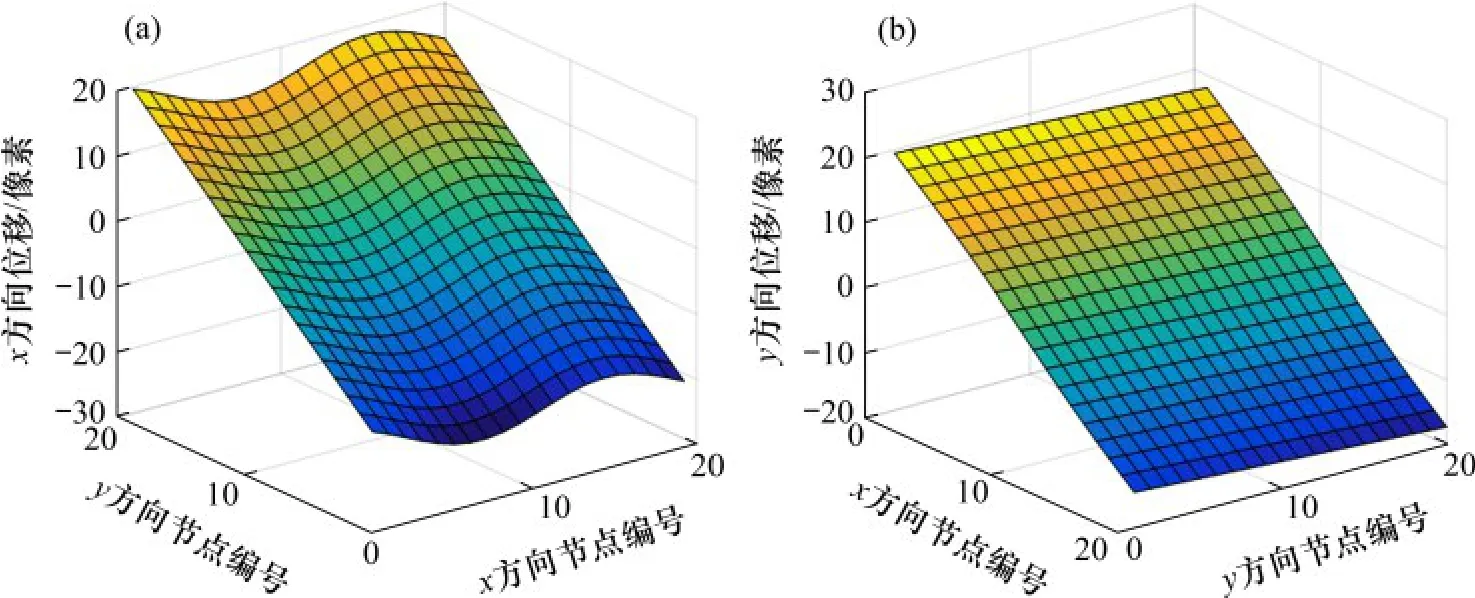
图4 匹配计算的位移场Fig.4 Calculated displacement field

图5 通过旋转图像计算得到的位移场Fig.5 Displacement field obtained by rotating image calculation

图6 插值引起的匹配误差Fig.6 Matching error caused by interpolation

变形图像是对原始图像旋转而来，因此，匹配偏差应该减半。使用双三次插值后进行匹配的偏差为±0.007 5 像素，为10-3量级，能够满足双目匹配与重建的测量要求。

3 高速旋转叶片的测量

以转速约为1 380 r/min的换气扇为对象验证所提方法的可靠性。测量方案和实验现场如图7 所示。试验使用2 台约克v611 高速相机，采集频率设为1 kHz，分辨率设为1 024 像素×768 像素，像元的长×宽为20 μm×20 μm，镜头焦距为35 mm，相机间距为37 cm，测量距离为80 cm，2台相机立体角为26°。使用2 个功率为200 W 的LED 灯补光，叶片单个状态转过8.3°。取1个周期共44个状态进行计算。布置相机时，应使叶片的旋转中心大致位于左右图像的中心。

三维变形的测量步骤[7]如下：

1)相机标定。使用基于摄影测量的相机自标定方法完成2个相机的参数标定。求解2个相机的内参数(包括镜头畸变、主点偏差和焦距)，右相机相对左相机坐标系的变换关系。

2)特征制备与图像采集。使用白色油漆和黑色记号笔在叶片表面制作散斑。开始测量后，先采集1 个静止状态作为基准状态，然后开启换气扇，待转动平稳后，双目相机同步采集1个周期的图像。

3)特征匹配。对采集的图像，使用本文提出的思路匹配变形序列。

4)三维重建。利用同一个状态下左右图像上的对应像点和双目相机的内外参数，重建所有节点的空间坐标。

5)位移场和最大主应变场的计算[19-20]。

3.1 SURF检测与图像校正后的匹配效果

任取1个旋转状态，对该状态和基准状态下的左图像进行匹配。测试SURF检测提供旋转参数的能力以及图像校正后的匹配效果。使用SURF算子检测到的初始特征点数为267对。对于少量的错误匹配对，将叶片旋转前后的图像看作是旋转相机拍摄静止叶片。使用RANSAC 估算基础矩阵，进而得到筛选后的点数为194对。旋转前后准确的特征点对用圆形标记并连接，如图8所示。匹配点全面覆盖公共区域的所有位置，不存在聚集抱团现象。根据匹配点对计算得到旋转角度为127.4°。实际的旋转角度大概为125°。可见，相机以小倾角观察小斜度的叶片，对旋转参数的求解影响不大。对变形图像顺时针旋转127°，在4个叶片上选择计算区域，子区尺寸为39×39，步长为10，总的节点个数为612，与基准图像相关匹配的结果如图9 所示。虽然经过双三次插值，但是旋转角度2°左右的2幅图像已稳定地匹配。

3.2 三维位移场与应变场的计算效果

图10 所示为1 个周期内叶片上单点在不同方向的位移场。单点的匀速圆周运动在任意直线上的投影理论上为简谐运动，因此，3个方向的位移均呈现正弦曲线。4个节点的起始极角相差约90°，因此，这4 条曲线的相位相差将近1/4 周期。而它们位于不同的极径上，且标定时坐标轴的原点并未与旋转中心重合，因此，幅值不同。

选取周期内有代表性的3个状态，自上而下分别旋转83°，182°和265°。不同状态下计算区域的综合位移场及应变场如图11 所示。由图11 可知，叶片的位移与极径成正比；在各个旋转角度下的最大主应变基本一致，应变最大值约为0.35%。叶片在旋转过程中表面的最大主应变分布较均匀，并不沿径向增大。

图8 SURF检测配对旋转叶片前后的特征点Fig.8 SURF detection of feature points before and after paired rotating blades

图9 图像反向旋转变换后匹配Fig.9 Image matching after reverse rotation transform

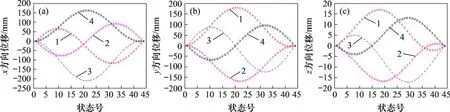
图10 各叶片上单点的位移场Fig.10 Displacement fields of single point on each blade

4 结论

1)使用双目立体视觉和数字图像相关法，提出了一种用于旋转物体全场位移及应变的测量方法，解决了高速旋转叶片的变形测量问题。针对叶片大角度旋转之后的图像去相关问题，提出用SURF算法进行特征点对检测和利用RANSAC算法进行准确点对筛选的匹配策略，将大角度旋转变形测量问题转换为常规的变形测量问题。

2)所提策略对变形与大角度旋转问题具有普遍适用性，变形较大时仍然能得出较准确的旋转角度，且使用双三次插值后进行匹配的偏差为±0.007 5 像素，能够满足双目匹配与重建的测量要求。

3) 以转速约为1 380 r/min 的换气扇为测试对象，通过所提旋转问题的匹配策略能够用于准确、鲁棒的旋转图像校正，并进一步通过数字图像相关匹配获得了扇叶旋转状态下的变形场和分布在4个扇叶上单点的位移、应变信息，证明所提方法能够用于旋转叶片的准确、全场测量。