可变阶数NURBS曲面的相机标定模型

徐立国 孙瑞东 党敬民

(1.吉林大学机械与航空航天工程学院， 长春 130022； 2.吉林大学通信工程学院， 长春 130022；3.吉林大学生物与农业工程学院， 长春 130022)

0 引言

摄像机视觉检测具有丰富的内涵(集颜色、尺度、方位、姿态等信息于一体)，在农用机器人领域备受关注。由于镜头的非线性，任何用于视觉检测的摄像机都需标定，标定精度直接关系到农用机器人执行任务的成败[1-3]。

标定方法的精度取决于所采用的相机数学模型，一些简单方法忽略了镜头的失真，相机的参数可以轻易地计算出来。直接线性法(DLT)由ABDEL-AZIZ等[4]提出，它用一个3×3转换矩阵描述由世界坐标系向像平面的透视变换。但对于高精度的应用场合，必须考虑镜头失真，建立非线性的投射模型[5-7]。考虑镜头失真的模型分为显式模型和隐式模型。

显式相机模型采用具有特定物理意义的参数描述相机的光学特性。在机器视觉中，常用的相机模型都是从针孔模型引申而来，为了补偿镜头失真可再引入附加参数。TSAI[8]的标定模型中通过引入2阶径向失真补偿来平衡线性投射和真实镜头投射的差异。ZHANG[9]引入了3阶、5阶的径向失真补偿。以上这些方法一般由几个参数即可对现有的相机进行有效标定[10]。SHEN等[11]应用传统的直接线性变换法(DLT)和非线性优化的方法，将相机拍摄的图像分为中心区域和边缘区域，并分别在这些区域单独标定相机。YAO等[12]运用BP神经网络的非线性优势，将文献[9]的算法推进到基因算法范畴。LIU等[13]利用3D球的影像建立相机的投影约束，求解了相机参数。LIU等[14]用纯二次曲线的影像作为媒介，获得相机参数。在机器视觉领域，研究者开发出一些针对多个相机的联合标定方法[15-17]。

然而，在显式模型标定中，必须预知相机的一些几何或光学特性才能获得较为精确的结果。虽然在一些应用中获得了较高的精度，但那只是局限于特定的视觉系统，且不足以补偿图像的局部失真和非常规失真。

隐式模型的标定方法将相机定义为一个“黑盒子”，试图将相机的输入、输出更直接地联系起来，本质上是建立世界坐标系物点传来的投射线和相机像平面上二维像素点之间的联系。因不需了解相机的预先知识，又不需计算其物理及光学参数，使得标定方法更为通用。GROSSBERG等[18]提出了一种通用模型，它给每一个像素赋予光学参数，可确定从像平面发出的射线位置和方向。徐赢等[19]提出一种应对大视场的非参数标定法，使相机沿横向以一定角度步进拍摄一条直线，相机转动90°后再依上述方法步进，得到了一个变形的直线网格图像，以此建立像素与物点的映射关系。HALL等[20]提出的三维标定模型包括两种方法，第2种方法直接采用多项式映射建立实物空间的三维表示。SRIKUMAR等[21]提出一种通用的相机标定模型，用相机拍摄3个相对位置未知的标定网格，找出对应于某一个像素点的3个标定网格点，基于这3个网格点必然在同一直线上建立线性约束，求解标定网格的相对位置，通过计算这3个网格点的视线而完成标定。双平面法[22]应用忽略失真的隐式相机模型，该方法在相机的可见范围内放置2个假想平面，双平面法的2个平面都是Z坐标为常数的平面，停留在直线的映射层面。由于线性映射限制了它的精度，GREMBAN等[23]将模型扩展为应用平方变换或三角形法处理失真信息。

CHAMPLEBOUX等[24-25]提出了几个平面的B样条法(NPBS)，实质上是双平面法的扩展。该方法把两个平面扩充为几个平面，以最小化一个线性约束为目标，一方面拟合数据点，另一方面平滑曲面。由于B样条曲面的优越特性，理论上可补偿任何连续失真。该方法只关注投射线与像素点之间的联系，不限定光学中心的唯一性。CHAMPLEBOUX模型采用固定阶数的B样条曲面，编程较为方便，但限制了其灵活性[26]。

本文提出可变阶数NURBS曲面的相机标定模型，根据应用场合的精度要求，阶数可调，并且可在不同的像平面区域应用不同阶数的NURBS曲面模型，以使得该模型适应性更强，而不需要过多增加求解难度和计算量。

1 模型建立

1.1 NURBS曲面方程

采用NURBS曲面代替双平面法中的平面。NURBS曲面的通用方程表达式为[27-28]

(1)

Q(u,v)表示自由曲面的空间坐标，是参数u、v的函数，式(1)右侧展开后是关于u和v的有理多项式。本模型中u和v的幂次相同，称为模型次数，幂次加1即模型阶数。对于NURBS曲面，控制顶点数等于u向阶数和v向阶数的乘积。通常根据对模型精度的要求确定控制顶点数，即确定模型阶数。控制顶点越多，模型阶数越高，精度也越高，但计算量随阶数上升而激增。本文所述m阶模型代表自由曲面在u向和v向具有m×m个控制顶点阵列。

Pi,j为控制顶点列向量(x,y,z)T，m×m个控制顶点的坐标决定了自由曲面形状。wi,j为权重，其值越大，自由曲面越靠近控制顶点。Bi,k(u)和Bj,l(v)分别是u向k次和v向l次的B样条基函数，它们的确定依赖于节点矢量。

参数u和v的定义域均为0～1。对于分辨率为800像素×600像素的相机，u向像素索引数为1～800，规范化后u在节点处可取值0，1/800，2/800，…，799/800，1；同理v在节点处可取值0，1/600，2/600，…，599/600，1；也是确定节点矢量的依据。本标定模型中u参数轴的方向与x轴相同(不要求平行)，v参数轴的方向与y轴相同。通过式(1)建立相机像平面内像素点和拍摄到的空间实物点的映射关系。

u向和v向的节点矢量分别为

U=[0=u0=u1=…=uk,uk+1,…，ur-k-1,ur-k=ur-k+1=…=ur=1]

(2)

V=[0=v0=v1=…=vl,vl+1,…,vs-l-1,vs-l=vs-l+1=…=vs=1]

(3)

u向和v向的节点矢量节点数分别为r+1和s+1，其中r=n+k+1，s=m+l+1。

节点矢量确定后，基函数计算式为

(4)

1.2 曲面拟合

两点可确定一条射线，由NURBS曲面的单值性可知，对任意像素点(u,v)，至少需要2个NURBS曲面才能确定世界坐标系中的对应投射线。对标定网格拍摄一幅图像，根据图像提取的信息可建立一个NURBS曲面，它代表像平面的(u,v)坐标向世界坐标系空间点(x,y,z)的映射。为获得NURBS曲面，首先需确定NURBS曲面多边形网格的控制顶点Pi,j。由于基函数是标量，坐标值可分别处理。Pi,j顶点的x坐标可用线性最小二乘估计求得[29-30]，即

(5)

(up,vp)——对应像素点的位置

因式(5)中的代价函数无光顺约束，所以计算是线性的，拟合曲面可以尽可能地靠近数据点。为了求解代价函数，需要足够的数据支撑。每个控制顶点的控制区域内至少注册1个数据点。

1.3 NURBS相机模型建立

当建立至少2个NURBS曲面后，像平面上(u,v)点所对应的投射线可由投射线与每个曲面的交点(x,y,z)确定。式(5)的最小二乘估算需要迭代算法，相机模型建模时可应用多于2个NURBS曲面；将多出的曲面数据结合前述2个确定投射线的曲面数据投入运算，可以加速运算的收敛过程，减轻在线计算的负担。NURBS曲面上点的坐标是控制顶点坐标值的线性组合；为了生成一个无误差的相机模型，多个不同曲面的对应控制顶点应该线性相关。因此，可以由不同曲面上对应的控制顶点拟合投射线，这些投射线与2个NURBS曲面相交。为避免坐标之间的比例舍入误差，投射线用参数方程表示为

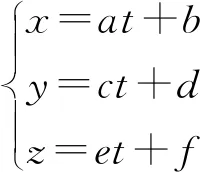
(6)

应用线性最小二乘法，由对应的控制顶点拟合出投射线方程，将投射线用于误差分析和模型阶数的切换。由此可建立一个双NURBS曲面模型，该模型唯一地确定了像平面上的像素点和投射线之间的关系，示意图见图1。

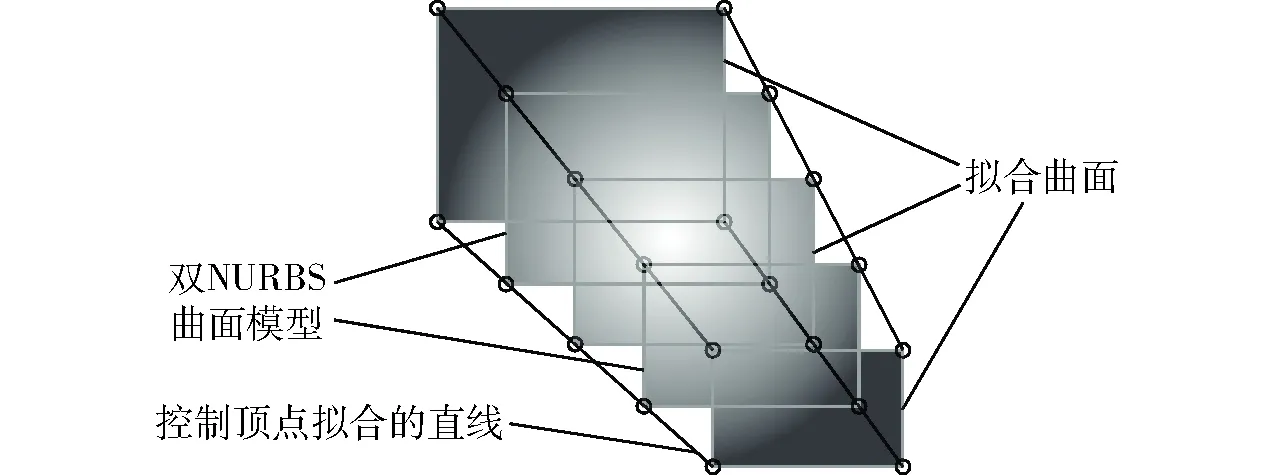
图1 双NURBS曲面模型Fig.1 Double NURBS surface calibration model

图1给出了5个NURBS曲面，分别对应于表1中5组数据(索引号是1、3、4、5、7)。这些曲面除Z坐标不同导致采样点数不同外，没有差别。选取索引号为3和5的两个曲面作为模型的双NURBS曲面，剩余的拟合曲面提供冗余的数据支持。

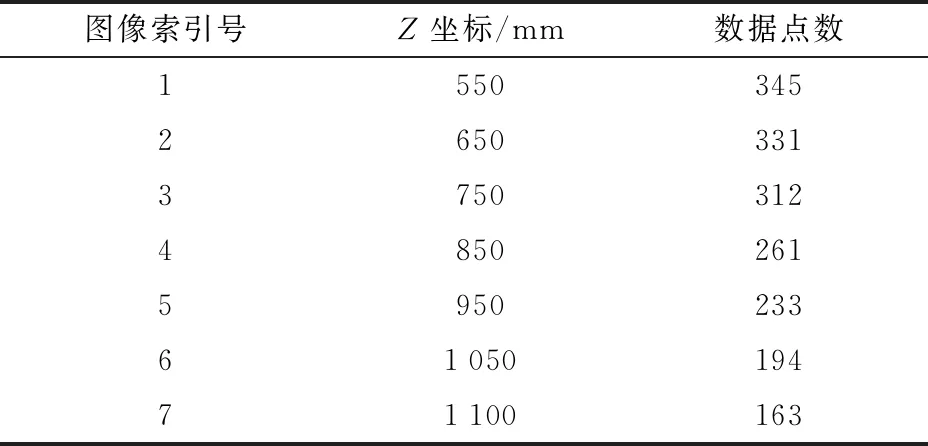
表1 采集图像数据Tab.1 Data acquisition of captured images

2 标定实验

实验基本设备有：直线滑轨、平面的标定网格和机器人夹持装置。夹持装置令机器人归“零位”，使标定实验具有可重复性。

2.1 数据采集

实验采用一台SEIKO工业级摄像机，分辨率800像素×600像素。世界坐标系固定于滑轨基座，使Zw轴平行于直线滑轨，见图2。在A0图纸上打印40 mm×40 mm的网格，将其贴在绘图板，绘图板垂直固定于直线滑轨，可沿Zw轴做500～1 300 mm范围的直线运动。在相机标定中，借助标定网格可同时获取空间点的阵列，从而提高工作效率。

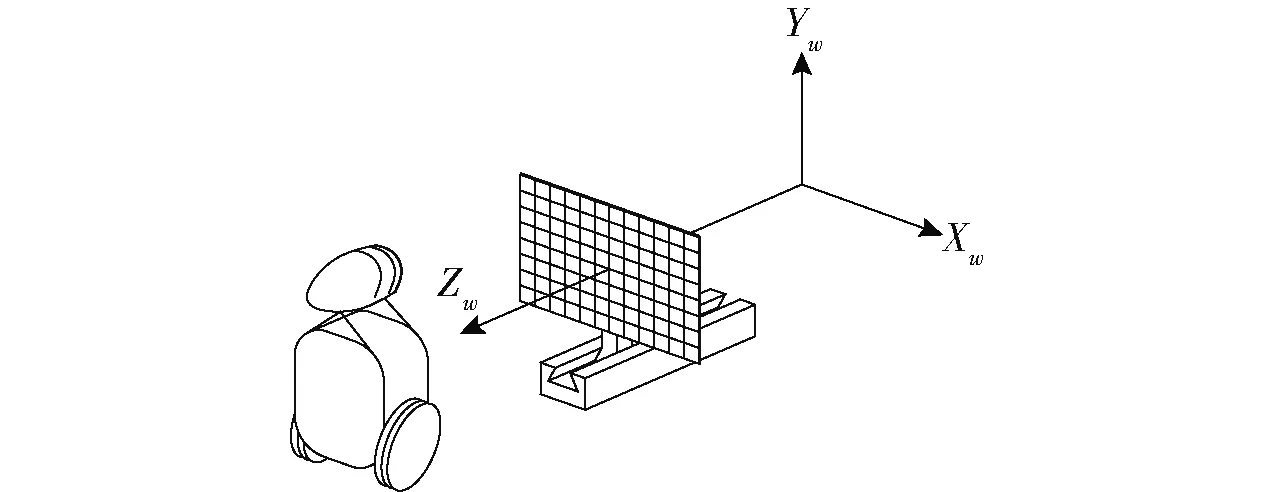
图2 标定网格、滑轨和世界坐标系Fig.2 Calibration grid，slide way and world frame

实验共采集7个不同滑动位置的标定网格图像，7个不同位置网格Z坐标见表1。对每幅图像进行交点提取，网格交点即检测数据点，网格交点提取见图3。获取的数据点集合见表1。机器人的相机面对Z轴方向放置；当标定网格Z坐标越大时，网格将越靠近镜头；使得相机在网格上的视野变小，捕获的数据点变少。

图3 图像的交叉点检测图(以方块表示)Fig.3 Crossover points detection of image (cubes)

2.2 两级NURBS曲面标定模型

对表1给出的7幅图像应用不同阶数的NURBS曲面模型进行拟合，以便获得最佳的阶数搭配。计算借助便携式计算机，处理器是Intel Core i7四核CPU@1.8 GHz 1.99 GHz，内存8 GB，64位操作系统，编程环境是Matlab 2018a。表2给出对采集的7幅图像进行4、5、6阶NURBS曲面拟合的时间对比。

索引号为2、6的图像用于误差分析。其他5个NURBS曲面，可以拟合对应于控制顶点的投射线。将这些投射线与预留的图像2、6曲面相交，就可以直接将相机模型求取的结果与图像2、6在标定板上实际测量值相比较，求得拟合误差。图像2和图像6不同阶数拟合误差见表3。

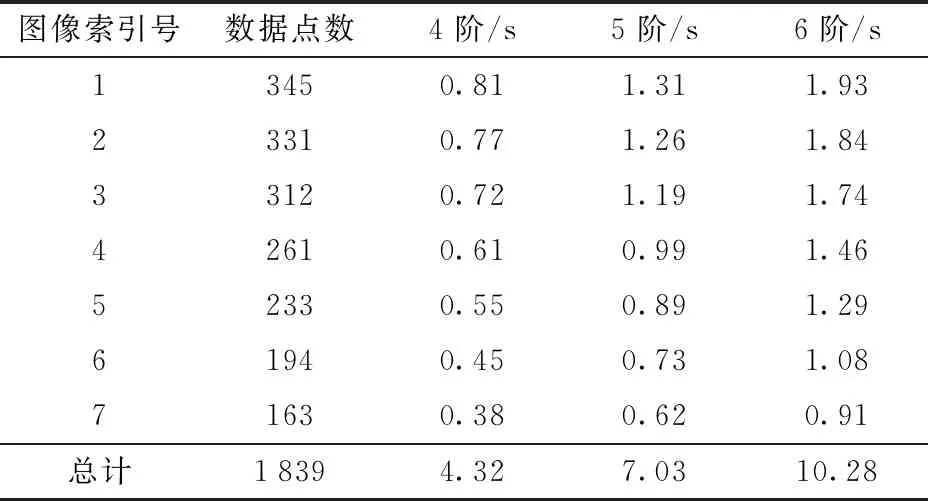
表2 不同阶数NURBS曲面拟合耗时Tab.2 Time consuming in NURBS surface fitting with different orders

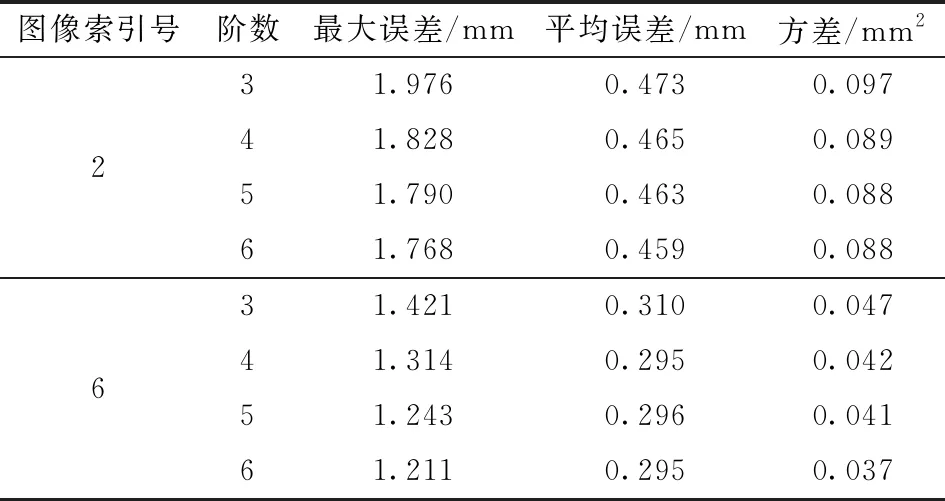
表3 不同阶数曲面的拟合误差Tab.3 Fitting error of different surface orders

由表3可知，6阶模型误差最小，但运算量太大。4阶与5阶模型具有较小的拟合误差。对比4阶与5阶模型可发现，5阶模型较4阶模型的精度提高有限，而4阶模型较3阶模型的精度提高较大。经以上分析可知采用3阶与4阶NURBS曲面建立相机模型可达到精度和计算投入的优化。

本实验中，图像1、3、4、5、7用于3阶与4阶NURBS曲面的拟合。得到2个(3阶、4阶)双NURBS曲面的相机模型，模型、投射线和像平面的对应关系见图4。

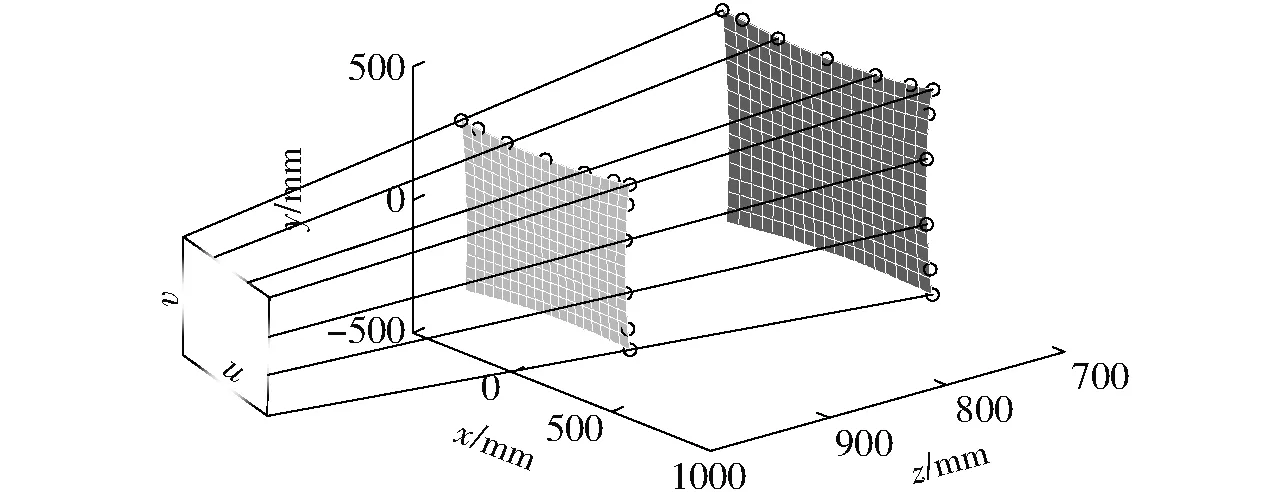
图4 像平面和双NURBS曲面的相机模型Fig.4 Image plane and double NURBS surface camera model

每一次曲面拟合都存在误差，表4给出了图像1、3、4、5、7的4阶模型误差，而3阶模型误差略大。

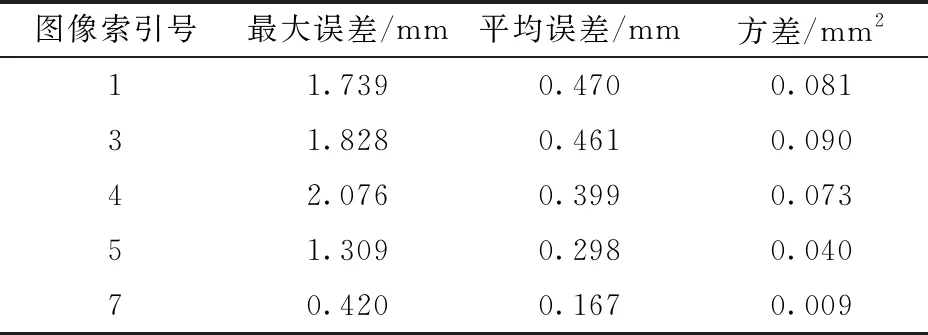
表4 曲面拟合误差Tab.4 Surface fitting error

2.3 标定误差

2.3.1双NURBS模型标定误差

在模型完全确立后进行标定误差分析。标定误差分析包含模型切换过程，切换方法见2.4节。如果把双NURBS曲面相机模型的2个拟合曲面分别设置于被测的标定板位置2和6，标定的误差等于真实测量的标定网格坐标减去由图像2(或6)中抽取的交叉点经标定模型反求得到的坐标值。

将标定误差定义为向量，得误差向量如图5、6所示；为了显示清晰，误差向量的幅值扩大了30倍。误差向量模(或称为标量误差)见表5。

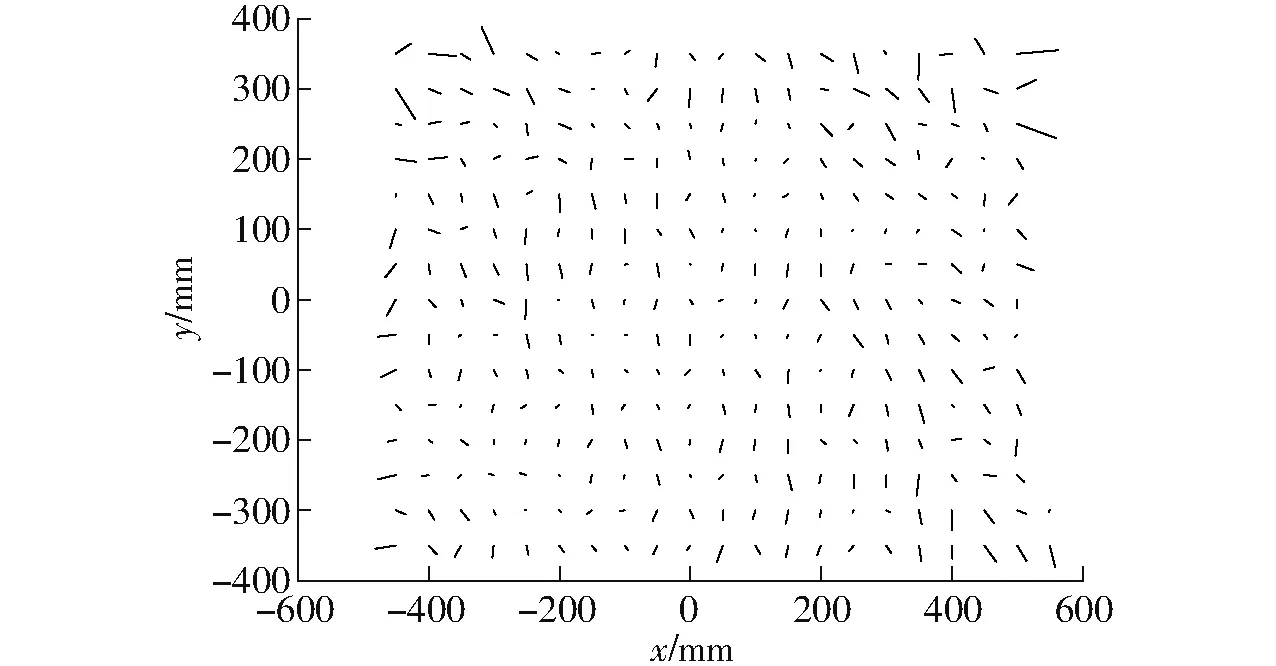
图5 模扩大了30倍的标定误差向量(图像2)Fig.5 Calibration error vectors of image 2 (30 times magnitude)

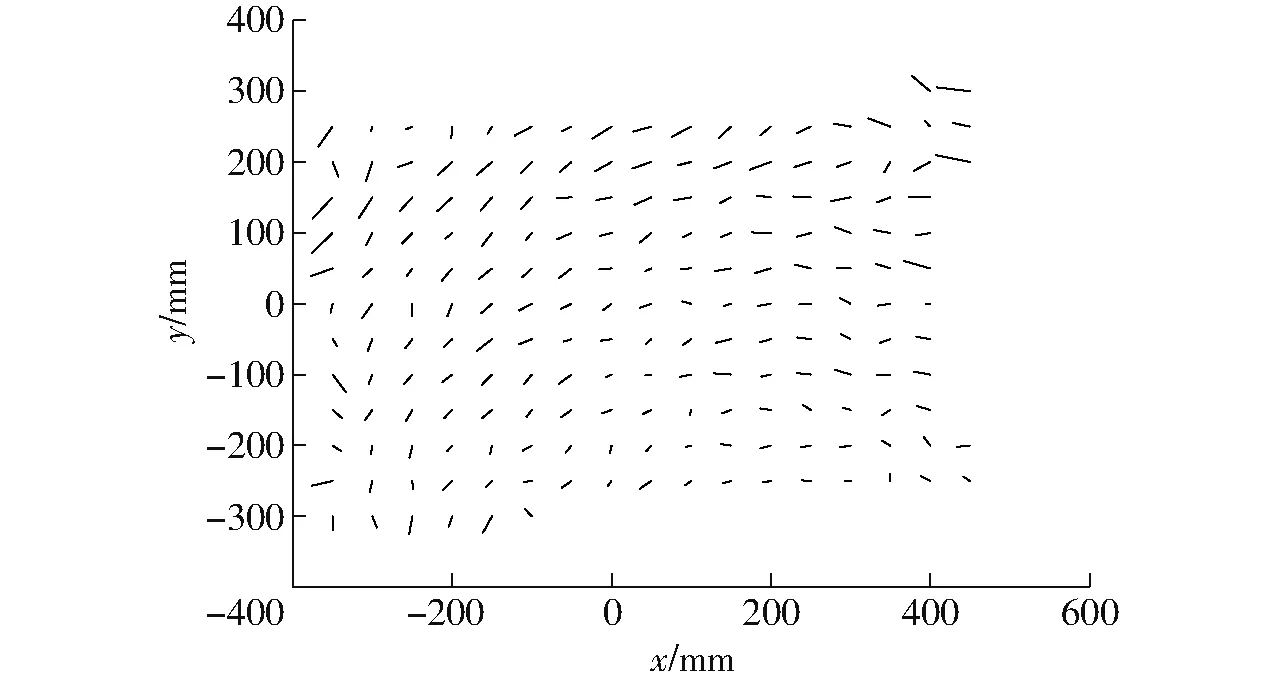
图6 模扩大了30倍的标定误差向量(图像6)Fig.6 Calibration error vectors of image 6 (30 times magnitude)

标定所产生的误差有多种原因：①不同曲面阶数的选择会影响标定精度。②相机的分辨率和交叉点提取的精度也会影响标定精度。如图3所示，在4个角处图像出现散焦，使提取的交叉点位置精度下降，会给图像处理带来困难。③必须指出数据采集的精度和可靠性严重影响相机标定模型的质量。标定板的平面度、标定板与滑轨的垂直度、网格的打印精度、空间点位的测量精度等都会影响标定结果。其他因素还包括用于实验的滑轨精度和标定板固定的牢固程度等。在7个测量位置的运动过程中，标定板可能出现偏移状况。

表5 标定误差Tab.5 List of calibration error

可见，精确的标定模型需要高精度的滑轨和更精密的标定板。经实验数据的误差分析，在世界坐标系Z坐标550～1 100 mm的范围内，标定平均误差不大于0.89 mm。

2.3.2与传统标定方法精度比较

标定误差严重地依赖于标定所用的设备精度和采样数据的精度，不同的评估方法也影响标定误差。应把标定模型置于同等实验条件下进行比较。

由于数学方法的相似性，本文提出的标定方法可转换为CHAMPLEBOUX的NPBS模型。以图像6的采样数据作为实验样本，按2.3.1节的分析方法，对NPBS模型进行误差计算，得到标定误差见表6，同时给出双NURBS法的误差。可知本文提出的标定法在3阶和4阶NURBS曲面方程之间切换，已超过了NPBS模型的精度。而CHAMPLEBOUX等[24]在实验中已经证明，NPBS模型在标定精度上明显优于双平面法。

表6 NPBS法与双NURBS曲面法的误差对比Tab.6 Calibration error of NPBS and double NURBS

NPBS方法在CHAMPLEBOUX的实验条件下精度会好一些，这也证明了实验条件对模型误差评估的影响。

2.4 不同阶数模型间的切换方法

由误差分析可知，采集图像的中心区域偏差较小，用较低阶数的标定模型即可满足应用精度要求；而在边角处偏差较大，需要用较高阶数的标定模型。本算法中预先建立两个标定模型，分别是3阶与4阶NURBS曲面的相机标定模型。先用3阶模型，按2.3.1节的方法对图像2和图像6进行拟合误差计算，以提供模型切换依据。

将像平面按参数(u,v)的一定间距均匀划分，划分示意图如图7所示。切换依据是：对每个区块内散落的交点误差向量求取模平均值。再用一个阈值将其二值化，即可得到切换模型的依据。图7中，区块中的数字表示该区块内模型的阶数。由于图像处理是以像平面坐标(u,v)进行索引，使得模型切换快捷方便。本实验只进行了两模型切换。规定多个阈值时可进行多模型间的切换。

图7 NURBS曲面标定模型的阶数切换示意图Fig.7 Sketch of order matching for NURBS surface calibration model

图7中，虚线是以像平面的参数(u,v)为依据均匀分区的示意图。分区的疏密程度取决于标定网格。用于多模型切换时，需增加网格密度，随之造成计算量的增加。事实上，相机镜头的失真是稳定的，分区计算只需标定时进行。对于图4中的双NURBS曲面模型，在2个NURBS曲面上的分区图可能会不同。

3 图像校正

图像校正是验证标定模型有效性最直观的方法，图像校正体现了视觉系统的测量精度。利用建立的相机模型把原来拍摄的图像2(没有参加建模)沿着视线反投射到任何表面都会形成一幅新的目标图像。如果投射到一个平面上，目标图像就会由于模型的补偿作用而消除相机造成的失真。

实验中，图像2被反投影到它原来的标定平面上，产生一个校正的目标图像，见图8。理想相机没有失真，即现实中的直线投射到像平面后应该还是直线。图2中的标定板上是均匀、正交的直线网格；

图8a图像是相机拍摄获得，出现了明显的桶形失真。图8b图像是经过标定模型校正的结果，直观上看所有弯曲的线都变成了直线，图像的网格更均匀，证明了标定模型是正确、有效的。

图8 双NURBS曲面相机模型对图像2的校正结果Fig.8 Rectifying result of image 2 using double NURBS surface camera model

4 结论

(1)提出了可变阶数NURBS曲面的相机标定模型。该模型不需要预知相机的光学特性，直接关联像平面上的点和世界坐标系中的投射线，可以隐式地修正镜头的失真。该模型具有分区选取NURBS曲面阶数的优点，优选曲面阶数后，可在像平面的不同区域应用不同阶数的NURBS曲面模型，达到运算量与精度的综合优化，使模型适应性更强。提出的可变阶数标定模型具有实际应用价值，通过适当匹配模型的切换阶数，可提升标定精度。

(2)采用双3阶和双4阶NURBS曲面的混合模型时，已经超过了NPBS方法的精度。在模型建立过程中，NPBS方法简洁，在视觉系统实际应用中，本文方法速度较快。

(3)虽然NURBS相机模型可获得较高的精度，但是与线性相机模型相比，NURBS模型在运算量方面无优势。如果对计算速度要求很高，可以预先计算出足够的采样点对应投射线，以满足在线计算NURBS曲面的要求。标定精度依赖于测量的精度以及选择适当的曲面阶数。实验表明，提出的标定模型能够满足农用机器人的应用精度要求。