导数一题多解 发散学生思维

洪 梅

(安徽省巢湖市第四中学 238000)

在导数教学中开展一题多解活动，不仅有助于学生更加全面地认识导数知识本质，而且可以拓展学生思维，使其积累相关的解题经验，不断提高其解题水平与解题能力.

一、一题多解在图象交点问题中的应用

图象交点是高中数学的重要问题之一.解答该类问题常转化为函数的零点或方程在给定定义域上根的个数问题.显然对于较为复杂的函数或方程问题，需要运用导数知识求解函数的单调性，以此来判断零点、根个数的情况.

例1已知函数f(x)=(2-x)ex，g(x)=a(x-1)2.(1)求曲线y=f(x)在点(0，f(0))处的切线方程；(2)讨论y=f(x)和y=g(x)的图象的交点个数.

该题目第一问较为简单，在这里不再赘述，接下来主要讨论第二问的两种解法.

方法一：含参讨论法

令F(x)=g(x)-f(x)，则F′(x)=(x-1)(ex+2a)，因a的取值未知，接下来需要进行分类讨论：

①当a=0，则F(x)=(x-2)ex，F(x)只有一个零点；

②当a<0，由F′(x)=0得x=1或x=ln(-2a).

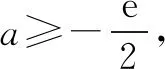
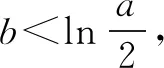
综上：当a≤0时，F(x)只有一个零点；当a>0时，F(x)有两个零点.

方法二：分离参数法

①当x=1时f(1)=e，g(1)=0，无解.

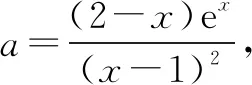
因此，当a>0时，y=a和h(x)的图象有两个交点.当a≤0时，y=a和h(x)的图象有一个交点.

二、一题多解在恒成立问题中的应用

恒成立是高中数学的热门题型，是高考的热门考点.解答该类题型的方法多种多样，需要具体问题具体分析.其中常用的解题思路为切线斜率法、分离参数法、含参讨论法等.

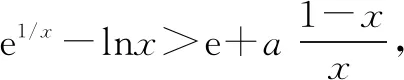
A.(0，e+1) B.(0，e+1]

C.(-∞，e+1) D.(-∞，e+1]

1.切线斜率法

2.分离参数法

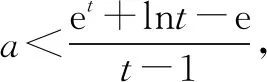
3.含参讨论法

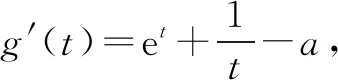
导数在高中数学中占有重要地位.教学中为提高学生解答导数问题的能力，应注重经典题型的筛选，积极组织学生开展一题多解活动，发散学生思维，深化学生对导数知识理解的同时，掌握更多的解题方法，不断提高其解题能力，促进其数学学习成绩更好的提升.