探秘立体几何的模型构建

曾 敏

(江西省南昌市江西师范大学附属中学 330046)

模型构建的本质是根据题意进行数学建模，提升空间想象能力.常见的立体几何模型有长方体(正方体)模型、圆锥模型、球模型、圆柱模型等.用构建模型的方式来看待立几问题，总结典型的立体模型，有助于提高解题能力.

一、长方体(正方体)模型

类型1 “三视图”中的应用

例1某几何体的三视图如图1所示，三个视图中的正方形的边长均为6，俯视图中的两条曲线均为圆弧，则该几何体的体积为____.

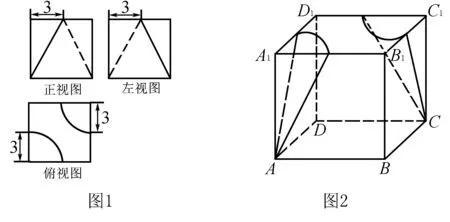
模型反思大部分几何体可通过对正方体或长方体分割得到，所以将三视图问题放在正方体或长方体模型中研究，能够快速得到直观图.

类型2 “补形”中的应用

解析依题可知PA2+PC2=AC2，∴PA⊥PC.

又∵PB⊥平面PAC，∴以PA,PC,PB为长、宽、高，作长方体如图3所示.

则该长方体的外接球就是四面体P-ABC的外接球，

模型反思观察条件与模型之间的内在联系，利用补形的思想可巧妙构造长方体(正方体)模型.如：①三棱锥的三条侧棱两两垂直，等效于一个“墙角”，可将“墙角”补形构造正方体或长方体；②三棱锥的三组对棱分别相等，等效于一个长方体的三条面对角线，可将三棱锥补形构造正方体或长方体；③正四面体补形构造正方体.

二、圆锥模型

例3 已知矩形ABCD，AB=2，BC=x，将△ABD沿矩形的对角线BD所在的直线进行翻折，在翻折过程中，则( )．

A．当x=1时，存在某个位置，使得AB⊥CD

C．当x=4时，存在某个位置，使得AB⊥CD

D．∀x>0时，都不存在某个位置，使得AB⊥CD

解析在翻折过程中，AB形成以BD所在直线为轴的圆锥侧面，作点A关于直线BD的对称点E，翻折过程中的垂直可转化为AB能与圆锥的一条母线垂直，结合模型知，最大张角是∠ABE，从而得∠ABE≥90°.即 ∠ABD≥45°.

模型反思翻折问题中，抓住共面的线性角不变的性质构建圆锥模型，借助模型量化计算，培养抽象思维与直观想象.

三、球模型

例4 已知四棱锥P-ABCD的底面为正方形ABCD，△PAD为等边三角形，且平面PAD⊥平面ABCD，空间一点M，满足PM⊥MC，则点M在底面ABCD上的轨迹是( ).

A.圆的一部分 B. 椭圆的一部分

C. 双曲线的一部分 D. 抛物线的一部分

解析如图5，空间一点M，满足PM⊥MC，则点M在以PC为直径的球面上.

又因为点M在底面ABCD上，所以点M的轨迹是球面与底面ABCD的公共部分，即交集为圆.故选A.

模型反思抓牢动点的轨迹符合球的结构特征(动点到定点的距离等于定值).

四、圆柱模型

例5 如图6，AB是平面α的斜线段，A为斜足，若点P在平面α内运动，使得△ABP的面积为定值，则动点P的轨迹是( ).

A.圆

B.椭圆

C.一条直线

D.两条平行直线

解析由已知可得动点P的轨迹在圆柱面上.由于AB是平面α的斜线段，所以平面α斜截圆柱面，得到的截面图形为椭圆.选B.

模型反思抓住动点的轨迹符合圆柱的结构特征(动点到定直线的距离为定值).

在探索立体几何的问题中，巧构立体模型，不但可以提升学生的思维起点，培养学生的空间想象能力，而且还能让学生发现数学美，体验数学美.