似是而非却又神机妙算的估算法

滕泽艳

(山东省平度第一中学 266700)

历年高考试题中，有相当一部分选择题甚至填空题都可以用估算法简捷地解决.下面通过举例进行说明，并对其解题一般规律进行归纳与整理.

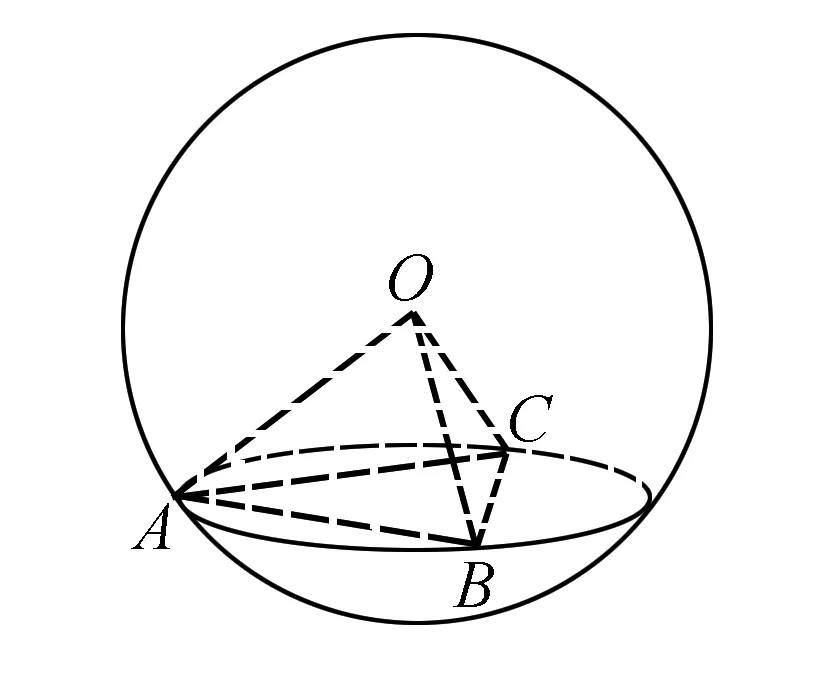
例1 已知过球面上A、B、C三点的截面和球心距离等于球半径的一半，且AB=BC=CA=2，则球面面积是( ).

解析选D.

解法一估算法.如图，2R=OA+OB>AB=2，故R>1，得S球=4πR2>4π，选D.

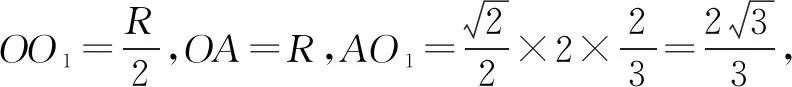
点评1.比较解法一和解法二，即估算法与直接法后我们不难发现，前者仅运用简单的大小比较(三角形两边之和大于第三边)即选出正确结果，思路清晰，回避了运算.

2.估算法体现了特殊与一般的数学思想方法.

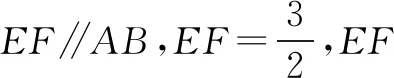
解析选D.

解法一估值法.

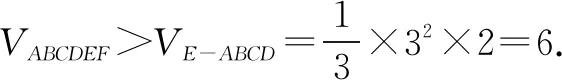
故排除A、B、C，应选D.

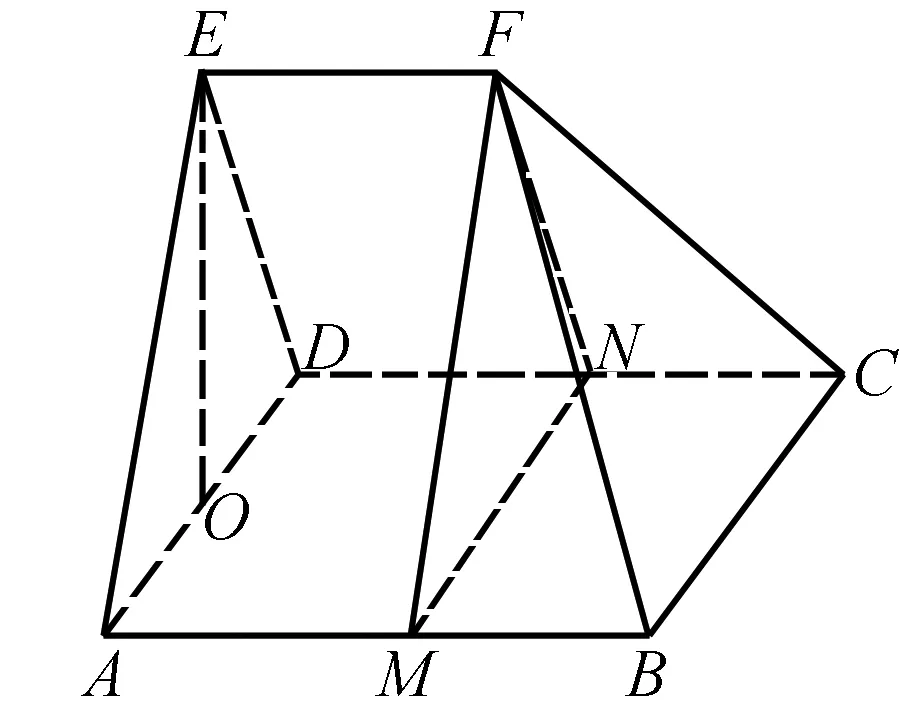
解法二特殊值法.

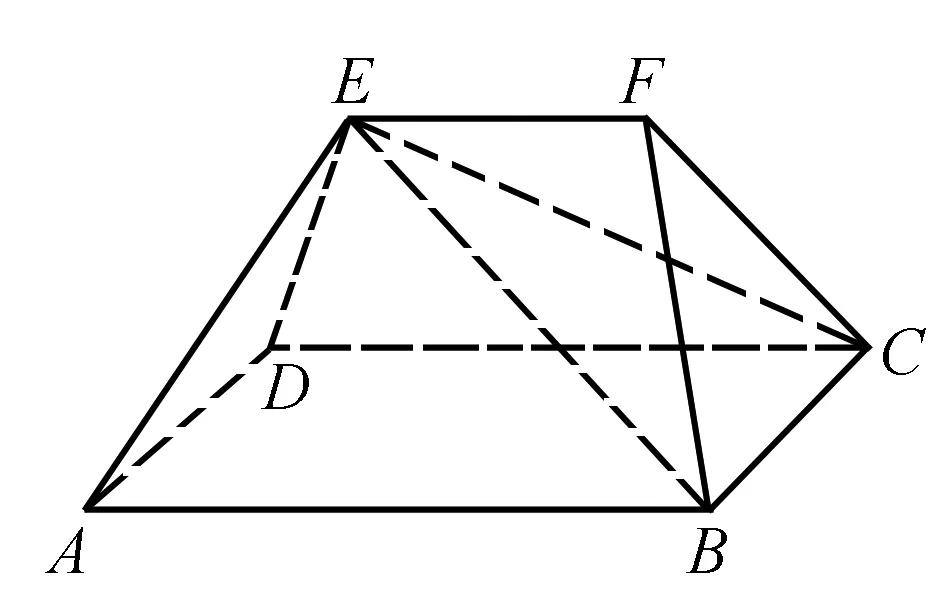
所以取特殊情况：即EF⊥面ADE，如图.取AB与CD的中点M、N，连接MF，NF，作EO⊥AD，垂足为O，则EO⊥平面ABCD.

∴VABCDEF=VADE-MNF+VF-MBCN

点评1.本题中的多面体是非典型的多面体，既非棱柱也非棱锥，直接求体积比较困难.解法一用易求的部分体积“四棱锥E—ABCD”估整体法，极其简捷.而解法二以特殊图形求解，由于四个选项均为定值，所以EF的位置并不影响结果，这样运算也非常简洁.

2.应用估算法解题的一般步骤为：

(1)根据问题条件，对数学对象(变量或图形等)进行特殊处理或缩放等；

(2)对处理后的对象进行计算；

(3)根据计算结果估计结论.

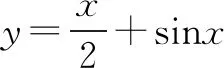
解析选C.

解法一估算法(取特殊点估算).

解法二估算法(以极限位置估算)

点评1.图形(图象)类选择题一般用排除法即可.可以从以下方面进行排除：

(1)特殊点的函数值；

(2)函数的奇偶性、单调性、周期性、对称性及极限(如渐近线)等.抓住其中其一个某一些性质即可进行排除.

2.估算法一般适用于不易直接求解或不易精确判断的数学问题.

例4 用1，2，3，4，5这五个数字，组成没有重复数字的三位数，其中偶数的个数共有( ).

A．24 B.30 C.40 D.60

解析选A.

解法二直接法

先排个位，从2与4这两个偶数中选一个有2种选法，再从余下的4个数字中任选2个排十位与百位(有序)，有4×3=12种，所以，共有选法2×12=24种.选A.

点评1.解法一巧妙利用奇偶数的对称性进行估算求解，简洁明了.

2.常见估算的方法有：

(1)以范围估定值：即不直接求出定值，而是通过研究所求元素的取值范围求解；

数形结合列代数式解题，或者反之，借助图形估算出数；

(2)以特殊估一般，即选取特例或特殊值对一般性问题进行处理；

(3)取近似值估算.