函数思想在高中数学解题中的应用
王 鹏
(江苏省徐州市铜山区郑集镇郑集高级中学 221143)
函数是高中阶段数学知识的一项重要板块,在生活形态中属于量与量之间的变换,能够为其它知识学习提供向导作用.为此,利用函数思想优化学生解题过程,提高解题能力,不仅是实现函数思想渗透的一种关键途径,更是高中数学教学的一大特色与魅力.
一、函数思想相关分析
函数是数学的基本概念,是函数思想发展的基础.因此,教师在应用函数思想辅助解题时,必须充分了解函数有关定义及性质,具体包括周期函数、单调递增/递减函数、奇/偶函数、一次函数、二次函数、指数函数(如图1)、对数函数(如图2)等,在此基础上体会函数思想.
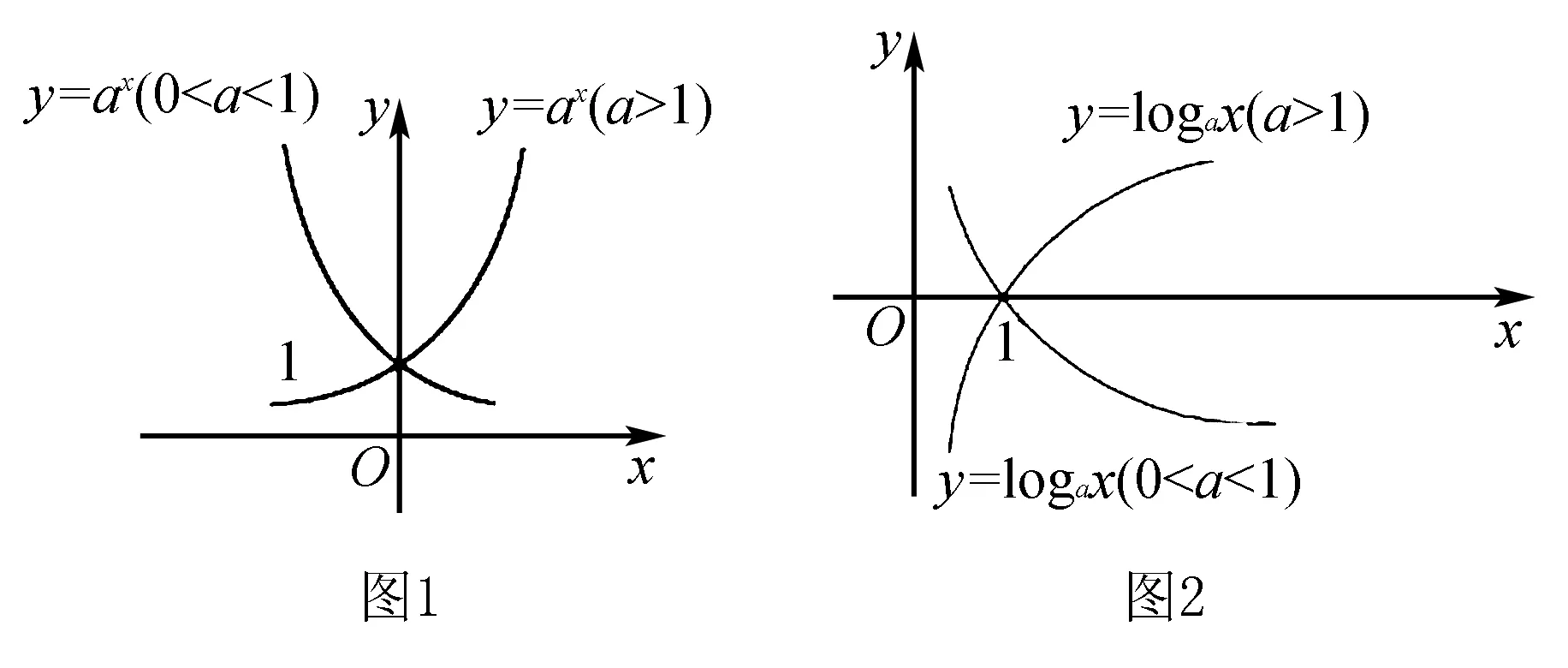
在高中数学中,许多知识中都体现了函数思想,包括方程、不等式、线性规划、随机变量、算法等,可谓是无处不在.在解题教学中,教师要注重分析不同知识与函数之间的关系,寻求函数思想运用的切入点.
二、函数思想在高中数学解题中的运用过程
1.引用函数单调性,求解不等式问题
函数与不等式属于两个性质完全不同的知识结构,在高中数学教学中,它们却有着密切的联系.不等式性质很大程度上反映了函数单调性.因此,在解题教学中,教师可以利用函数思想引导学生用函数的观点审视不等式,更好地把握不等式本质特征.为此,在笔者看来,不等式中最值与恒成立问题是函数思想渗透的切入点.相关例题如下:
例1对任意x∈[-1,1],f(x)=x2+(a-4)x+4-2a的值大于零恒成立,求a的取值范围.
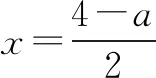
2.引入函数解析式,求解数列问题
高中阶段学习的等比、等差数列本就是一类自变量为正整数的特殊函数,与函数思想有着密切的联系,不同的数列问题中无形中会隐藏着函数的某种特征.利用函数思想求解数列问题也是历年高考中的重点考题.利用函数思想求解数列问题的途径有很多,比如求解等差数列前n项和的最值问题时,可以将Sn看做关于n的二次函数,运用配方法,引入函数单调性知识解决问题.为了从“形”上帮助学生充分认识函数思想与数列知识之间的关系,本节以函数解析式的运用为例,分析相关数列问题的求解.
例2已知a1=1,a2=a3=a4=0,求数列{an}的通项公式.
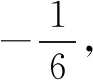
3.引入函数与方程联系,求解零点问题
函数思想是处理“数学型”问题的一种思维方法,描述的是现实生活中数量之间的变化关系.在问题解决中,从实际情境中建立对应函数模型,运用函数基本知识,实现问题的解决.方程类知识在教学中也孕育了函数思想,它的本质在于研究问题在运动中的等价关系,一般情况下习惯首先明确给出的未知量与已知量之间关系,通过构建方程或方程组,由未知量推导出已知量.虽然两者看起来本质不同,但在实际操作中常常互相渗透,函数间的关系与方程之间可以互相转换.
例3已知函数f(x)=xlnx-ax2-x(a∈R),讨论函数f(x)的零点情况.
通过审题发现,函数f(x)并不是所熟悉的函数模型,解析式包括对数、幂函数,此时需要首先确定函数定义域x∈(0,+).接下来引导学生对原函数进行变形,变为f(x)=x(lnx-ax-1)(a∈R),同时用g(x)表示“lnx-ax-1”,二次变形为f(x)=xg(x).因为x≠0,因此对函数f(x)零点的讨论可以转为对函数g(x)零点情况的讨论.解题过程进行到这一步时,引入函数思想中与方程之间的联系,将对g(x)零点的讨论等价转化为讨论方程lnx-ax-1=0的根的情况.但方程仍然不是我们熟悉的方程,此时可以重新从函数角度进行审视,将方程转化为的形式,求解与y=a交点横坐标,从而得出原函数f(x)的零点情况.
综上所述,函数思想在高中解题过程中的运用,不仅展现了函数知识与其它板块知识之间的联系,还为解题提供了新思路,有利于培养学生创新意识,提高解题能力.为此教师要重视函数思想的渗透,优化解题过程.

