异质投资者结构下的股权溢价研究
唐伟敏,唐雨潇,杨灏野
(1.中南财经政法大学 会计学院,湖北 武汉 430073;2.华泰证券(上海) 资产管理有限公司,上海 200120;3.中山大学 国际金融学院,广东 珠海 519082)
一、引言
Lucas考察了只有一个商品条件下纯交换经济中均衡资产定价的随机行为[1]。在该经济中,每一消费者都最大化同样的效用函数,经济中单一商品具有不同单位的生产成本。一个资产定义为某一单位的全部或部分权益,每一单位的生产随时间随机波动,资产的均衡定价也是如此。上面所描述的经济就是所谓“表示性代理人”(representative agent)模型问题。就和CCAPM模型一样,在该模型中每单位资本消费和典型投资者的消费流呈完全正相关。当资本市场完全时,个体可以和市场中任何或有事件进行交易。由于每个人的行为都是相同的,结果任何个体的消费流就会同每单位资本的消费流呈完全正相关。股票和债券有着近似的经济自然状态,所以,两者应该有着类似的收益率。事实上,他们通过应用标准的定价理论估算了进行风险调整以后的股票收益率,平均而言,股票收益率应该至多比无风险债券高1%。
然而,对历史数据的实证研究发现:过去的一百年间美国证券市场中的实际收益率(剔除通货膨胀)达到7.9%,而同期的无风险债券的收益率只有大约1%,两者的差额为6.9%。而对二战后的统计,两者的差异更为惊人,几乎达到8%。高的股权风险溢价,低的无风险利率和平滑的消费合起来很难用一个看起来合理的投资者风险规避水平来解释,也就是说实际数据和经典的金融理论产生了矛盾。 Mehra和Prescott把这个问题称作“股权溢价之谜”[2]。
事实上,股权溢价不仅仅存在于美国市场,英国战后的溢价为4.6%,其他主要资本主义国家如德国、法国、日本都有类似的结果[3]。Fernandez等对大约82个国家进行研究也有类似的结果[4]。对中国的市场进行检验,依然发现股权溢价现象的存在[5],而新兴市场的股权溢价更为严重[6]。
股权溢价自提出之时起便一直是金融经济学和资产定价理论的重要前沿课题,在经济资源配置、经济福利以及货币经济政策和资本投资决策方面都有重大的理论和实践意义。
所以,试图解释股权风险溢价问题便成为经济学和金融学研究的一个重要课题。这之中有偏好替代、修改效用函数、 不完全市场、税收监管、 短视下的损失厌恶等[7-11]。每一种对Mehra和Prescott模型中假设的改变都能部分解释股权风险溢价问题,但 Mehra认为问题远没有得到解决[2,12]。
在中国许多学者对股权溢价之谜问题做出了有益的研究。李治国和唐国兴证实了中国股票市场存在股权溢价现象[5];汪昌云和汪勇祥从股权风险溢价的视角对现代资产定价理论进行系统的回顾和梳理[13];肖俊喜和赵向琴等分别运用已有模型和理论对中国市场中的股权溢价进行相关检验和解释[14-15];李巍和姚秋萍运用中国证券市场进行了股权溢价的宏观经济学解释[16]。总体上,中国学者的研究主要分布在理论综述和实证分析上,模型构建和理论分析相对缺乏。
在经典的如CAPM模型世界里,投资者结构常常被忽略,因为在经典模型中总是假设投资者是同质的。当投资者是异质的时,我们往往将之定义为投资者之间的信息不对称或不同的信息禀赋。的确,信息不对称能帮助我们解释风险资产价格为什么经常偏离其“合理的”价格,但它只能解释价格的短期运动,因为信息从长期来讲总是趋于对称的。“股权溢价”被证实为一种长期的存在,所以要合理解释 “股权溢价”问题应该假设信息是对称的且是完全的。
当投资者是同质时,试图解决“股权溢价”问题的有效方法就只能是改变投资者的效用函数,引入极端概率分布和改变约束假设了。
许多经济学家和金融学家已经意识到:市场的基本面是由资产及其价格的供给和需求所共同决定的。即使从实证的角度来看,证券市场的价、量之间的联合动态所揭示的资产价格和其它经济要素信息也比单纯的价格波动所揭示的市场信息广泛得多,所以任何完善的资产定价模型必须能建立股票价、量之间的动态联系。因此本文将设定投资者是异质的,股票的均衡价格由市场出清所决定。
Harrison和Jeremy考虑了存在动量交易者时市场过度反应和轻度反应的情形[17]。他们假设市场中存在两类有限理性的交易者:消息观察者和动量交易者,每一类人拥有各自可利用的公开信息的某一子集。消息观察者关注一些私人信息,但不能从价格中提取其他消息观察者的信息,消息观察者不会因为过去的或现在的价格变化而调整目标。而动量交易者却只根据价格变化而调整他们的交易策略,其预测只是过去历史价格的简单函数。当信息在消息观察者中逐渐扩散时,会伴随着价格的轻度反应,动量交易者会因此而获利,但动量交易者不断运用该简单策略时,价格就会形成长期反转。
消息观察者类似于价值投资者,而动量交易者的存在也被许多实证研究文献所证实。如策略交易,技术交易等本质上就是动量交易者。
本文设定投资者是异质的,对交易者的划分的术语采用Harrison和Jeremy的分类称谓,但有着不同的模型表述[17]。
结合传统金融理论,假定:
1.市场是完全的。
2.市场的信息是对称的、有效的。
3.市场中存在两类交易者:消息观察者和动量交易者。交易只发生在两类投资者之间,交易成本为零。
4.两类交易者效用函数是标准的、相同的,风险厌恶系数、 时间折旧因子也是相同的。
5.市场的信号为股票历史价格和该股票红利水平。
6.股票的均衡价格由市场出清所决定。
本文试图从一个全新的视角解释股权溢价现象。通过建立均衡资产定价模型,求模型的均衡解,进行模型解的静态分析。股权风险溢价由三部分组成:投资者的风险补偿、投资者对红利的不同处理方式所引致的价差和由价格动量的偏差所引起的溢价。我们给出了前两部分的一个一致上界估计,这个上界估计不足以解释已被证实的股权溢价程度,通过第三部分贡献可以合理解释任何程度的股权溢价现象。
二、模型
考察一简单经济,资本资产市场的禀赋为一定数量之股票(风险资产)和无风险资产,无风险资产利率为r。市场中有两类投资者:动量交易者和消息观察者。市场中的信息为股票历史价格和公司红利流水平。动量交易者进行投资决策时以历史价格为主,消息观察者进行决策时则更注重公司红利流水平。两类投资者的比例分别为ω,1-ω,(0<ω<1)。经济设置定义如下:
1.偏好。假设所有投资者都具有不变绝对风险规避系数(1)该假设是为了使得模型解存在。(CARA)。在此偏好下,投资者对风险资产需求和其财富无关,这表明均衡股票价格与投资者的财富分布无关,也和他的总财富水平无关。其消费和投资策略是最大化其生命效用。
其中,Et是条件期望算子,Ct+s是第t+s期的消费,所有的投资者都存在同样的时间折旧因子β和风险厌恶参数γ。
2.信息。在第t+1期,历史价格的信息为Pt,Pt-1(2)这里假设投资者对股票历史价格的关注只是第t 期和第t-1 期,也可以将其改为从第t-k 期到第t期,两者本质上是一致的。。
红利信息为当期红利:Ft+1≥0。是一个随机变量,假设它服从以下过程:
Ft+1=DFt+εt
(1)
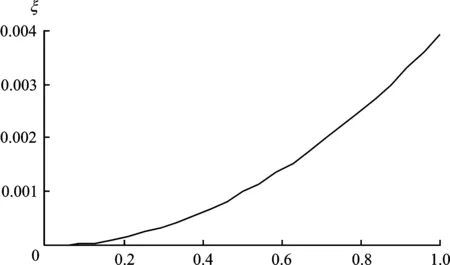
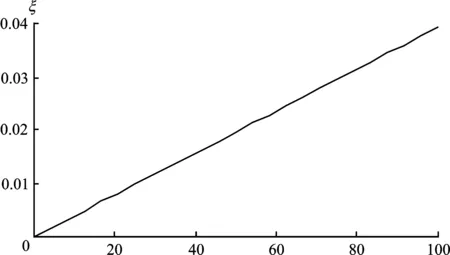
其中εt是白噪声。0 在第t+1期:投资者的信息为Pt,Pt-1,Ft+1。 3.投资者的信息处理。假设投资者是有限理性的。本文中投资者有限理性的定义有别于通常情形。由于本文的信息对称的结构,两类投资者对市场信号的提取不存在差异,所以对投资者的异质性定义为其对信息处理方式的不同。两类投资者中,动量交易者更愿意以股票的历史价格为主要信息依据,而消息观察者则以公司红利为主,历史价格为辅。投资者总是固守这种思维模式,这是对Harrison Hong和Jeremy文中两类投资者根据公司消息和股票的历史价格独立操作假设的一种改进。 投资者对市场价格的预期存在差异:消息观察者对价格的预期中公司红利部分所占权重要比历史价格部分大;而动量交易者对市场价格的预期中更注重股票的历史价格。 由于市场的信息为Pt,Pt-1,Ft+1,可以假设第t+1期的均衡价格为: Pt+1=Pt+AΔPt+BFt+1 (2) 其中ΔPt=Pt-Pt-1,A,B为待定系数。 由于投资者的有限理性,其对股票价格进行预期时两类信息所占的权重不同。 假设动量交易者对价格的预期(记为Em(Pt+1))为: Em(Pt+1)=Pt+A(1+W)ΔPt+B(1-W)E(Ft+1)(3)也可以将ΔPt和Ft+1前面的系数分别改为A(1+W1)和B(1-W2),0≤W1,W2≤1。此时,模型的解是类似的。并不影响本文的经济解释。本文的假设只是使得模型解更为简单。 (3) 其中0≤W≤1。 消息观察者的预期(记为En(Pt+1))为: En(Pt+1)=Pt+A(1-W′)ΔPt+B(1+W′)E(Ft+1) (4) 其中0≤W′≤1。 式 (3)和式(4)是本文模型假设的中心所在。投资者的异质性定义为投资者处理信息的方式的差异,他们以各自不同的方式来预测股票的未来价格。 式 (3)和 式(4)测度了他们预测股票下期价格时赋予该股票历史价格变换和红利流变化的不同权重。当W,W′→0,两类投资者趋同,市场中的投资者退化为同质的,本模型也退化为“表示性代理人”模型。 经典的模型认为股票价格运动服从于随机游走过程,即股票价格运动和股票历史价格变换无关。但Jegadeesh和Titman发现从中期来看,即如果以3到12个月为观察周期时,股票的收益率呈系列正自相关[18]。Bondt和Thaler发现长期而言,股票的收益率呈系列负自相关[19]。上一个五年中的收益率最低的股票投资组合在下一个五年中收益率最高,反之亦然,这表明股票价格运动存在着某种趋势。 更进一步,即使是市场有效且信息对称时,如果投资者是有限理性的,或者由于投资者能力不足,对信息的处理存在偏差,这些偏差必然会反映在股票的历史价格中,当投资者预测股票价格运动时,股票历史价格仍然有一定参考作用。 假定股票交易严格发生在两类投资者之间。市场出清的条件将会自动产生均衡价格。 5.记λ=(1-ω)W-W′,易知-1<λ<1。假定-1<λ≤0,该假设是为了保证模型解的经济学意义,后文中将讨论(4)为了得到模型的分析解,一些数学上的约束也是必要的。。 本部分将推导模型的均衡解。 记投资者t+1 期的超额收益为Qt+1,则: Qt+1=Ft+1+Pt+1-RPt 其中R=1+r。由式(3)和式(4)可得动量交易者在第t+1期的期望超额收益为: Em[Qt+1]=E(Ft+1)+Em[Pt+1]-RPt =gE(Ft+1)-rPt+A(1+W)ΔPt (5) 其中g=[1+B(1-W)]。 消息观察者在第t+1期的期望超额收益为: En[Qt+1]=E(Ft+1)+En[Pt+1]-RPt =g′E(Ft+1)-rPt+A(1-W′)ΔPt (6) 其中g′=[1+B(1-W′)]。 给定上述设定,可以求出两类投资者的最优持有组合。 它有下列解: 其中g=[1+B(1-W)],g′=[1+B(1-W′)] 证:考虑下面试验解: (7) (8) (9) 式(9)最优投资-组合策略的一阶条件为: 其中: (10) 将式(10)代回Bellman方程得: lnα-αWt-(aE(Ft2)+bE(Ft)+k) (11) 注意到式(11)是一个恒等式,所以有: 解之得: 证毕。 定理2在上述市场结构下的市场均衡价格为: 证明:由定理1,可知动量观察者的最优持有策略为: g=1+B(1-W) 消息观察者的最优持有策略为: g′=1+B(1+W′) 为了推导均衡时的价格函数,市场必须出清。 1=ωχt+(1-ω)χ′t (12) (13) (14) 由式(13)~(14)解之得: 所以均衡价格为: (15) 由式(15)可知:在t+1期时的均衡价格由这几部分构成: 第t期的价格Pt; 上期价格成本利率补偿为: 以及剔除红利部分为: 一种特殊的情形值得注意: 当两类投资者趋同时,即变量W,W′都趋于零时,由式(15)得: Pt+1→Pt+rPt-Ft+1 (16) 将式(16)进行递归,假定当t→时,Ft→0 两边求期望得: (17) 式(17)恰好表达了一种经典的资产定价结果,当市场信息对称并且投资者是同质时,证券期望价格为该证券未来期望红利流的折现值之和。 可以这样来理解上述结论:由于模型假设交易只发生在两类投资者之间,当投资者是同质时,没有交易发生。此时,投资者无限期持有该股票(组合),该证券(组合)的收益就只能来自股票(组合)的未来收益,即红利。因此,股票的预期价格是该股票的内在价值,即该股票未来期望红利流的折现值之和。 该结论表达了本文模型与传统模型的兼容性和一致性,即本模型是传统模型的一种有效拓展。 “股权溢价”所表达的是股票持有者期望获得的超过无风险资产的收益率的平均幅度。为什么风险资产的收益率要远远高出无风险债券呢? 定义:投资者结构为市场中两类交易者对信息的不同处理方式及其权重的组合,测度投资者结构的向量为(ω,W,W′)。 由式(15)有: (18) (1+W-ω[W+W′]) 记股权溢价为ξ: (19) (20) 式(19)给出了股权溢价和Pt+1、Pt及各个参数之间的动态关系,可以将其理解为一种特殊的资产定价公式。 股权溢价是由三部分构成的: 3)(u-1)r,是由两类投资者处理信息时对价格动量偏差的差异所引起的。 下面讨论都是基于式(19)之上。式中的每一部分都被测度投资者结构变量(ω,W,W′)所决定。 定义:记λ=(1-ω)W-ωW′,为股权溢价的临界值,易知-1<λ<1。 λ值的变化同股权溢价的变化有着密切的联系。 溢价仅仅是因为风险吗?为什么股票的收益率要比无风险收益率高得多呢?一个直觉的答案就是既然股票具有风险,投资者需要较多的 “溢价”以补偿额外的风险。当溢价仅仅是因为风险时,资产定价就会变得简明,它就更容易被应用于投资者的交易策略和投资者的投资组合策略。当投资者同质时,这是一种经典的结论。 性质2:当ω=0,W=0时λ=0,股权溢价与风险成正比。 注意到当ω=0 时,市场只有消息观察者,且W=0时,消息观察者趋于理性,所以模型退化到传统金融理论的模型世界中,此时股权溢价与风险成正比,股票价格的定价公式类似于CAPM模型。 例一:令r=2%,ω=0.5,γ=0.4,Pt=50,σ2=25,则股权溢价为ξ=0.55%。股权溢价与动量交易者权重的关系见图1,股权溢价与股票风险关系见图2。 r=2%,W=W′=0.5,γ=0.4,Pt=50 σ2=25图1 股权溢价ξ与动量交易者权重ω的关系图 r=2%,ω=0.5,W=W′=0.5,γ=0.4,Pt=50图2 股权溢价ξ与股票风险σ2的关系图 当测度投资者的结构的变量呈现更一般的情形时,风险只是构成股权溢价的一部份。本文中基于投资者结构对股权溢价的讨论都是一种充分条件,而非充分必要条件。 性质3的结论是简明的,它给出了股权溢价的一个充分条件。市场中投资者结构决定了两类投资者信息处理方式的差异和两类投资者在市场中的权重,不同的投资者结构对应着不同的均衡价格。当市场中投资者结构呈现一定的特征时,即测度投资者结构的变量ω、W、W′满足一定的条件时,无论市场的基本面如何,无论投资者的风险规避系数的大小如何,股票市场是一定会发生股权溢价现象的。 引理1:若0≤W,W′≤1,0≤ω≤1,则N≥4。由引理1可以得到: Pt=20,γ=1,r=0.01图3 风险对股权溢价贡献的上界估计图 性质4的结论是简单而强有力的。当投资者是异质的、有限理性时,风险对股权溢价贡献随着投资者结构的变化而变化。然而,无论投资者的结构如何变化,性质4给出了风险对股权溢价贡献的一个上界估计,这个上界和投资者的结构是无关的。这说明当投资者具有正常的风险规避系数时,由投资者结构变更所引致的风险对股权溢价的贡献是有限的,由风险所导致的溢价并非股权溢价的全部,不足以揭示 Mehra和Prescott的实证发现[2]。 (21) (22) (23) r=0.01,Pt=25,σ2=25,Ft+1=1图4 股权溢价ξ与投资者风险规避系数γ的关系 由式(17)、式(22)可以看到当动量交易者的权重ω越大时,构成股权溢价的(u-1)r部分对股权溢价的贡献就越大。 记u为投资者结构对股权溢价的贡献系数。图5~7给出了式(23)不同参数下的三维图形: ω=0.75, 0.02≤W≤0.1,0.88≤W′≤0.98图5 投资者结构对股权溢价的贡献系数的三维图形(1) ω=0.85, 0.02≤W≤0.1,0.88≤W′≤0.98图6 投资者结构对股权溢价的贡献系数的三维图形(2) ω=0.95, 0.02≤W≤0.1,0.88≤W′≤0.98图7 投资者结构对股权溢价的贡献系数的三维图形(3) 通过图5~7三个三维图形,可以看到:当ω越大,即动量交易者的权重较大时,构成溢价的一部分(u-1)r对股权溢价的贡献就越大。当0.02≤W≤0.1,0.88≤W′≤0.98,ω=0.75时,u最大值为3.74。ω=0.85,其他参数不变,u最大可为14。而当ω=0.95,其他参数不变,u最大则可达到80,此时“股权溢价”非常严重。更有一种极端的投资者结构的情形:当ω→1,W→0,W′→1时,u→。此时市场上几乎都是动量交易者,而且他们都是极端的价差追逐者,换言之,他们都漠视股票的基本面(红利),他们的交易策略仅根据股票 的历史价格,此时,股权溢价会达到极致。 该情形在假设中被排除,这是因为: 由定理一,可知消息观察者的最优持有策略为: g′=1+B(1+W′) 当0<λ<1时,g′<0,这就得出,当期望红利流越高时,消息观察者的持有策略越下降,这是有悖经济学常识的。 长期以来,对股权溢价问题的探讨一直是金融理论的一个中心话题。试图解决该问题的任何一种方法和模型都是一种对金融市场的模拟和描述,其实质包含了研究者对金融市场的认知和对金融理论的理解。 模型坚持市场信息对称和完全的设定,坚持一种正常的市场经济、信息分布的设定。部分模型引入较极端的假设,如罕见性灾难事件、极端概率分布等,这可以部分解释股权溢价现象,但这些假设缺乏稳定性。模型中假定投资者具有正常的风险偏好和效用函数,部分模型运用其他风险偏好替代,或修改效用函数,但从模型构建角度来讲,这些函数的性质不如经典理论模型中的各类标准函数。模型引入了投资者结构的概念,两类不同交易者的交易策略,即投资者对市场信息的不同处理方式及两类投资者的权重生成了投资者结构,充分考虑了证券市场的微观基础。华尔街以及中国证券交易市场有句谚语:涨时重势,跌时重质,就是对模型投资者结构定义的一种有效阐述。模型的假设总体上是稳定合理的,模型对股权溢价的解释视角也较为新颖,有一定的原创性。 研究发现,理论上风险溢价与投资者结构相关,风险及股票的基本面对股权溢价的贡献随着投资者结构的改变而改变。然而,上述贡献是有限的,模型能给出这两部分的一个上界估计,这个上界估计与投资者结构无关。可以看到当动量交易者权数较小时,仍然可能发生股权溢价,只是程度较小,而且当动量交易者的权数较小时所形成的溢价不足以揭示实证的风险溢价的结果,因之可以推断:产生严重股权溢价的重要原因是市场中存在大量的动量交易者。 模型试图证明动量交易者的权重较大时,股权溢价会较为严重。Donadelli和Prosperi发现新兴市场的股权溢价更为严重[6]。虽然没有专门的实证结果表明新兴市场中动量交易者权重相对较大,但一般认为发达成熟的市场中消息观察者即所谓价值投资者的比例较大,所以模型对于新兴市场的解释是合理的。 对于中国市场,一般认为动量交易者占比较大。按照模型结论,似乎中国股市应该享有较高的股权溢价,许多文献却发现中国不存在股权溢价或程度较低[14],但赵向琴和袁靖研究发现中国市场1996—2014年间平均股权溢价达到8.64%[15]。对中国股权溢价程度的实证研究之所以有较大的差异,可能和研究样本的选择和研究方法的差异有关。还有一点值得思考:导致中国股权溢价程度较小的最主要原因之一是由于中国股票市场存在发行价、市盈率虚高的现象,例如中石油(股票代码601857)及许多创业版股票等,这从另一个角度验证了中国证券市场发行制度或许有着某种程度的不合理。 模型对股权溢价的静态分析尚未完全展开,后面可以做进一步的分析。结合模型对中国证券市场进行动量交易者的测度和实证是本文未来的研究方向之一。
三、均衡
(一)超额收益
(二)最优持有组合

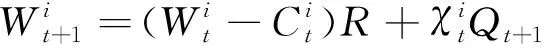
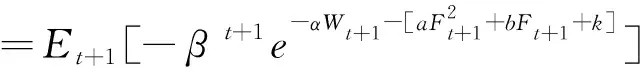




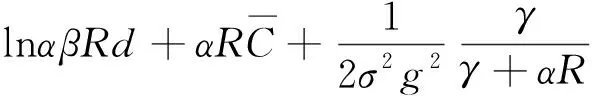

(三)均衡价格分析


四、为何股权溢价



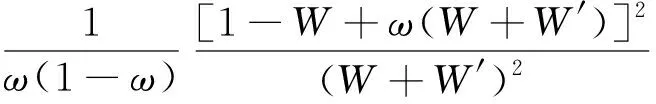

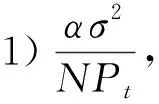

(一)当λ=0时
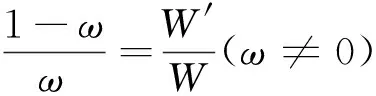
(二)当-1<λ<0时



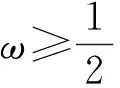




(三)当0<λ<1时

五、结语

