《百分数》单元的纠错教学例谈
庄晓纯
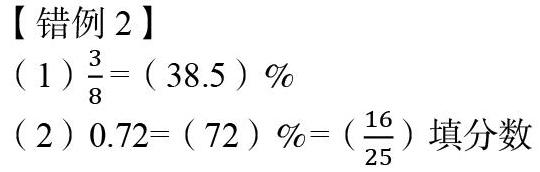

摘 要 《百分数》单元的学习中学生错误频发,通过深入分析出现错误的根本原因,提出引导学生自主纠正错误的改进策略,加强学生对百分数意义的正确认识和理解,提高学生解决百分数实际问题的能力。
关键词 百分数的意义;百分数、小数、分数的互化;百分数实际问题
中图分类号:G622 文献标识码:A 文章编号:1002-7661(2020)23-0194-02
百分数是一种特殊的分数——分母是100的分数,百分数的认识和应用是小学阶段数学学习的重要内容之一。现实生活中,人们也习惯运用百分数来刻画、描述事物的定量化特征,交流、传递社会发展的信息。百分数对于小学生来说既熟悉又陌生,熟悉的是学习百分数之前,学生已有了学习整数、小数、分数的基础,学生在日常生活中或多或少接触过百分数;陌生的是由于百分数的特殊性,学生难以深入透彻地理解百分数的意义,尤其是百分数的实际问题比较抽象复杂,学生往往分析不清数量关系,导致无法解决较为复杂的百分数实际问题。
以下笔者列举三类《百分数》单元教学中学生常见的错误,分析错误的根本原因,谈谈引导学生自主纠正错误的策略,以提高学生对于百分数的理解和应用。
错误类型一:百分数的意义理解不清
【错例1】
(1)一堆煤有(97%)吨,运走了它的75%。
(2)120粒黄豆全部发芽了,发芽率是120%。
(3)六(1)班今天出勤48人,请假2人,缺勤率是(95.8)%。
错因分析:第(1)题,学生没有理解百分数的实际意义是两个量之间的倍数关系,百分数的后面不能加单位名称,应该填小数或分数表示煤的质量。第(2)题,学生对发芽率的概念认识不清楚,发芽的种子颗数÷总颗数=发芽率,发芽率最多只能是100%,不可能超过100%。第(3)题错误的原因是学生对出勤率的概念没有真正理解,出勤率是指出勤人数占全班人数的百分之几。学生把48人当成了全班人数,用(48-2)÷48×100%来计算出勤率,出勤率是48÷(48+2)×100%=96%。
改进策略:教学中教师首先引导学生理解百分数的意义:百分数表示的是两个数量之间的倍数关系,与原来学习的“一个数是另一个数的几倍”“一个数是另一个数的几分之几”的意义类似,分母是100是为了便于比较两个分数的大小。同时教师要从学生的实际生活出发,引导学生搜集身边熟悉的事例或数据,如优秀率、合格率、发芽率、成活率、出勤率、绿化率、城市的森林覆盖率等,通过互相交流,体验和理解百分数在现实生活中的广泛应用。
教学反思:百分数的概念来源于丰富的生活经验,学生通过对大量百分数实例的观察、理解、对比、辨析,体验从具体情境中抽象出百分数的过程,发现百分数与其他数的相同与不同点,真正感受百分数存在的合理性,理解百分数的实际意义。数学概念的教学要从直观到抽象,教师要通过生动鲜活的例子开阔学生的视野,帮助学生真正理解知识、运用知识。
错误类型二:百分数、分数、小数的互化错误
【错例2】
错因分析:这两题学生出现错误的根本原因是虽然了解了百分数、分数、小数互化的方法,但是运用不熟练,常见的百分数、小数、分数的大小认识不清,甚至个别同学对于、这样的分数对应的小数和百分数都不知道,每次互化时都要列竖式,而且计算频频出错,这样的学习基础如何解决各种百分数问题呢?
改进策略:针对出现的问题,教师引导学生整理了常用的百分数、小数、分数互化的内容,整理如下:
教师引导学生观察特点,寻找规律,并进行分段集中记忆、背诵、默写,加以强化,尤其是个别基础知识较为薄弱的学生,反复记忆,再练习相关的题目,对于没有整理到的不常见的百分数,需要强调互化的方法。如,分数化成小数,用分子除以分母;小数化成百分数,把小数点向右移动两位,再在末尾添上百分号等,通过有针对性地练习,以提高学生做题的正确率和速度。
教学反思:数学的学习需要记忆吗?答案是肯定的。记忆是人的大脑对外界输入的知识进行重新编码、保持和再现的过程,数学概念、公式、解题模型都需要记忆才能加以运用。《数学课程标准》明确指出:注重学生对基础知识、基本技能的理解和掌握。试想,如果学生头脑中没有清晰的20以内的加减法、表内乘法口诀、面积体积公式等大量的基础知识,那么数学的学习岂不是无源之水、无本之木?当然,我们倡导的记忆不是简单的死记硬背,而是在理解的基础上进行记忆,不断引导学生积累数学基础知识,掌握基本技能,培养良好的数感,才能熟练应用于实际问题的解决中,从而达到数学学习的融会贯通。
错误类型三:百分数实际问题数量关系分析错误
【错例3】
(1)盛荣超市第二季度销售额为165万元,第二季度比第一季度增加了10%。第一季度销售额是多少万元?
列式解答:165×(1+10%)=181.5(万元)
(2)一种电冰箱原价3500元,第一次降价10%,第二次又降价10%,这种电冰箱现价多少元?
列式解答:3500×(1-10%-10%)=2800(元)
错因分析:找错单位“1”是百分数和分数解决问题中最常见的错误。第(1)题单位“1”的量是未知的,求单位“1”用除法计算,第一季度销售额是165÷(1+10%)=150(万元)。而第(2)题学生错误的原因在于缺乏生活经验,不能准确理解折扣的含义,第二次折扣时单位“1”发生了变化,指的是第一次折扣后的价格。电冰箱的现价为3500×(1—10%)×(1—10%)=2835(元)。
改进策略:单位“1”是题目中数量之间比较的“标准”,它是解决百分数问题的出发点和支点。在教学百分数的实际问题时,首先引导学生通过认真审题,找出题目中的关键词:“是”“占”“相当于”一个量的百分之几,从而找准单位“1”。根据题目数量间的内在联系,学会运用线段图或用列方程的方法解决问题。
教学反思:随着年级的升高,解决问题的条件复杂多变,很多学生面对错综复杂的条件束手无策,教师要引导学生反复读题,理解数量之间的关系,寻找不同的解题途径。如画图、列方程、假设等,拓宽学生的解题思路,学生经历从不同角度探求分析问题和解决问题的方法的过程,体验解决问题策略的多样性,丰富数学活动的经验,提高解決实际问题的能力,发展数学思维,提升数学素养。
参考文献:
[1]徐玲玲,小数练习中学生错误的原因及改进策略[J].小学教学参考,2018(11月中旬).
[2]王银.数学审美:超越数学思维的教学智慧[J].江苏教育,2018(2).
[3]《全日制义务教育数学课程标准(修定稿)》2013版.

