基于贝叶斯方法的突发水污染事件溯源研究

孙 策，李传奇，白 冰，杨 圭，王 茜

(1.山东大学土建与水利学院，济南 250061；2. 山东省水利综合事业服务中心，济南 250013)

随着我国工业化进程与城市化进程的不断加快，公众对于生态环境安全的需求不断提升，但与此同时各类危化用品的不断使用导致突发水污染事件频发。自2012-2017年我国突发环境事件2 657 起，其中突发性水污染事件占95%以上[1]。事件成因主要包括污染物违规排放、生产事故泄露、自然灾害等[2]。目前，我国突发水污染事故的研究主要集中在水环境质量监测、污染事件预警与快速模拟、风险评估、处置技术、应急决策支持等方面[ 3]，对突发水污染事件精准溯源的研究相对较少[4, 5]。河流突发性水污染事故溯源，也称为污染源识别定位问题，或源参数识别。其基于监测的浓度数据，追踪定位进入河道的污染物质的来源，寻找出污染源泄露节点、泄露时间、泄露强度等污染源的关键信息。

实际情况中想要实现污染物精准溯源是十分困难的，传统的识别模型需要大量的先验信息，以污染物的泄露历史，污染物衍生的化学产品以及精准的事故环境监测数据作为支撑[6]。然而在水环境监测中，想要实现对各类污染物空间位置全覆盖式的实时监控，是极不现实的。因此用具有代表性的几个监测断面的监测数据来反映整个监测区域水环境的水质情况是最常见的监测方法。如何利用有限的监测数据，反演出污染源位置等关鍵信息，这就需要一套行之有效的追溯污染源的方法。现有的识别方法主要有直接法、优化法和概率统计法[7]。直接法通过及时反演控制方程，重建观测污染物的历史分布，解决了溯源问题。李云良等[8]用粒子示踪耦合模型，并结合野外粒子示踪实验来调查鄱阳湖洪水期污染物迁移路径；优化方法则通过最小化污染物浓度观测值与预测值的差值，从而得到污染源参数的识别值。汤雪萍等[9]利用移动水质监测平台，结合行为规划法和浓度梯度法进行污染源定位识别；概率统计法通过对事件的发生概率进行估计，不断改进基于似然函数的识别值来识别污染源的参数，主要方法有贝叶斯推理、最小相对熵等。朱嵩等[10]建立了基于贝叶斯推理的反演数学模型，进而求解水动力-水质耦合数学模型的点源强度与位置的联合识别。

本文基于贝叶斯-蒙特卡洛方法，采用适用性更强的M-H采样方法和GIBBS采样方法来处理二维污染物排放的溯源问题。并对M-H采样方法做了一定的改进：在每一次根据建议分布生成样本值时，增加一个判断样本值是否满足于后验概率密度函数的条件，以使根据建议分布生成的样本值更快更准确地趋近于真实值。最后运用算例对比分析了两种采样方法各自的优点，并分析了两种采样方法在计算精度和计算维度上的差异性。

1 研究方法

1.1 污染物扩散模型

依据质量守恒原理和连续性法则，河道中任一点污染物扩散及对流基本方程式为[11]：

(1)

式中：C(x,y,z,t)为t时刻控制体积单元内污染物的浓度，mg/L；xyz为坐标位置，m；t为污染物排放时长，s；k为污染物降解系数，s-1；ux、uy、uz分别为污染物沿xyz方向的平均流速，m/s；Dx，Dy，Dz分别为污染物在x，y，z方向的弥散系数，m/s；S为源汇项。

由于三维模型求解复杂，且污染物在垂向扩散速度远小于横向扩散，因此可将三维模型转化为二维模型[12]。

(2)

由于实际河流受到河岸影响，污染物在水体中的扩散受到边界限制并产生反射，将其作为影响因素，此时污染物浓度的解析解为：

C=C1+C2+C3

(3)

式中：C1,C2,C3分别为污染源、近岸边反射、远岸边反射在点(x,y)处产生的质量浓度增量，其各自的计算表达式为：

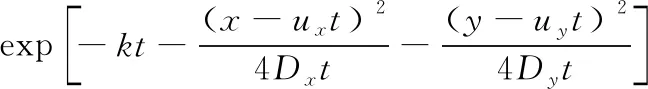
(4)

(5)

(6)

考虑到河流宽度一般较大，所以假设岸边的反射次数为1次[13]，即n=1，b=0，此时得到污染源下游河段断面上污染物浓度随时空变化的规律为：

(7)

式中：m为污染物排放总量，g；B为河道宽度，m；其余符号意义同前。

在一定的温度范围内，k1与温度关系的表达式为：

k1=k20θ(T-20)

(8)

式中：k1,k20为温度分别为T℃和20 ℃时的耗氧速率系数，d-1;θ为温度校正因子，为无量纲经验系数。一般情况下，当温度为10～37 ℃时，校正因子取1.047。

河流中的垂向扩散与明渠流中的扩散相似，可采用对数流速分布形式，得到河流垂向扩散系数：

Dz=0.067hu

(9)

(10)

式中：h为河流平均水深，m；u为河流摩阻流速，m/s；i为水力坡度；g为重力加速度，m/s2。

对于顺直的河流，FUSCGER[14]收集了多个实验资料，统计得到横向扩散系数平均值的估算式为：

Dy=0.23hu*

(11)

若流速分布资料缺乏，可采用经验公式粗略估算纵向扩散系数。FISCHER[15]提出经验公式：

Dx=0.11u2B2/hu*

(12)

1.2 溯源方法

在贝叶斯统计的情况下，所有未知参数都被视为随机变量，它们的分布是从已知信息中得出的[15,16]。因此，贝叶斯统计为不确定性分析提供了严格的方法，可为管理决策提供关键信息[17]。贝叶斯推理基于以下公式[18]：

(13)

式中：p(X|Y)为X的后验概率分布函数，表示获得观测值Y后参数X的分布规律；p(X)为先验概率分布函数，表示由资料及经验获得的参数X的分布规律；p(Y|X)为似然函数，表示模型参数与观测值的拟合程度。

但是未知参数的后验分布一般为复杂的高维非常见分布，要实现对这些分布的直接计算十分困难，这就使得贝叶斯推断方法应用于实践中时受到很大的限制。然而，近几十年来，蒙特卡罗方法，特别是马尔可夫链蒙特卡罗(MCMC)算法，已被应用于获得参数的数值总结[19]。

在统计学中，马尔可夫链蒙特卡罗(MCMC)方法是一类基于构造一个马尔可夫链的概率分布抽样算法，该马尔可夫链具有理想的平稳分布[20, 21]。其基本思想是对比较复杂或无明确数学表达式的概率分布p进行抽样，得到一个大量服从p的随机向量序列，并通过建立合适的抽样算法使该序列满足马尔科夫链的性质，即新状态的参数只依赖于目前的参数状态，而与之前的参数状态无关[22]。

基于此，溯源问题可以转化为对后验概率密度函数的抽样问题。在贝叶斯方法的基础上构建出待反演参数的后验概率密度函数，依赖于MCMC方法对其进行抽样。本文采用适用性较强的M-H采样方法和Gibbs采样方法进行采样，两种方法的基本思路及步骤如下[23]。

M-H采样方法步骤：

(3)生成新的参数状态下模型的模拟结果，计算模拟值与观测值之间的纳什系数(NSE)；

(4)产生一个0～1间均匀分布的随机数u，若α>u且NSE满足提前设定的精度范围，则xi+1=x*，否则xi+1=xi，且i值加1；

(5)重复步骤(2)～(3)，得到一系列参数的抽样值，进而可进行参数后验规律的统计。

GIBBS采样方法步骤：

(4)按顺序依次从相应条件概率分布中得到每一个参数新的抽样值；

(6)重复步骤(2)～(5)，得到一系列参数的抽样值，进而可进行参数后验规律的统计。

可以看出，M-H采样方法和GIBBS采样方法在生成新的参数状态时有着很大的不同。M-H采样方法每次给所有参数一个新的状态，且生成新的参数状态时借助于建议分布，故为了判断建议分布选取的合理性，每一次采样都要通过计算接受概率判断是否接受该状态。而Gibbs采样方法则借助于已知的条件概率分布逐次生成每一个参数新的状态，通过坐标轴的轮换采样来确保每一次采样的合理性。

2 结果分析

为方便计算，此次研究中以点源岸边污染物瞬时排放为例对M-H采样方法和GIBBS采样方法进行计算，以对比分析两种方法各自的优越性及其之间的差异性。此次研究选取长约8 500 m，宽约1 200 m的河段作为研究对象，纵向和横向的水流平均速度可以利用涡轮流速仪测得，ux=21.6 m/min，uy=0.3 m/min，横向扩散系数 和纵向扩散系数 由所测数据代入式(7)、式(8)计算得到。同时河段的水体深度h取1.0 m，通过查阅资料得到模拟污染物的罗丹明B在类似环境的河流里的降解系数k=0.1 d-1。河段的水文水质参数如表1和表2所示[24]。设定在河流某断面发现污染情况的时间为初始监测时间，随后每隔25 min监测1次，共得到12个该断面的监测数据。

表1 河流已知水文参数表Tab.1 River known hydrological parameter table

表2 河流待反演水文参数表Tab.2 River to be inverted hydrological parameter table

2.1 溯源结果分析

将表1及表2的数据代入公式(3)，可以得到研究中监测断面的污染物浓度观测序列，如图1所示。可以看出观测断面污染物的浓度近似于正态分布，最高值约在开始观测后的第110 min。需要进行反演计算的未知参数有污染物排放位置x(以观测断面为坐标原点，污染物排放量m，污染物排放时间t(为距离首次得到污染物浓度数据的时间)。本研究采用上下限区间的均匀分布作为待反演参数的先验分布。其对应的先验分布概率密度函数分别为：

(14)

(15)

(16)

为了更符合现实情况并证明选用算法的适用性，可以在污染物观测数据上叠加一个观测误差，这里设定观测误差εi=Ti(m,x,t|X)-Yi服从正态分布N(0,0.52)，设θ=(m,x,t)为待反演参数，因此考虑了误差概率分布的似然函数可定义为：

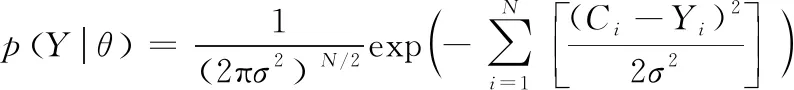
(17)

此时污染源参数的后验概率密度函数可表示为：

(18)

式中：P(θ)为待反演参数的先验分布；σ为观测误差所服从正态分布的标准差；N为观测点得到的浓度值个数；Yi为观测点测得的浓度值大小；ci为根据污染物扩散模型模拟出的观测点污染物浓度理论值大小。

图1 观测断面污染物浓度序列值Fig.1 Observed section pollutant concentration sequence value

分别采用M-H采样方法和GIBBS采样方法对待反演参数的后验概率密度函数进行抽样计算，为得到较稳定的抽样结果，对两种方法均迭代计算了2 万次，抽样的结果如图2及图3所示。

由抽样结果可以得到，M-H采样方法的抽样结果分布很紧凑，污染物排放位置确定为距离观测断面4 500 m，污染物排放时间距离第一次在观测断面得到污染物浓度100 min，污染物排放量在1 t附近。而GIBBS采样的抽样结果分布接近于正态分布，污染物排放位置在4 400～4 600 m，污染物排放时间为距离第一次在观测断面得到污染物浓度的95～105 min，污染物排放量0.99～1.01 t，但每一个未知参数分布的峰值与M-H采样得到的结果是较一致的。

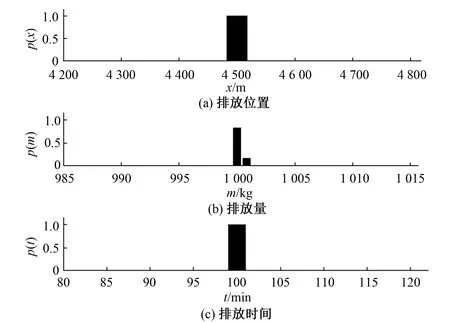
图2 M-H抽样结果Fig.2 M-H sampling result

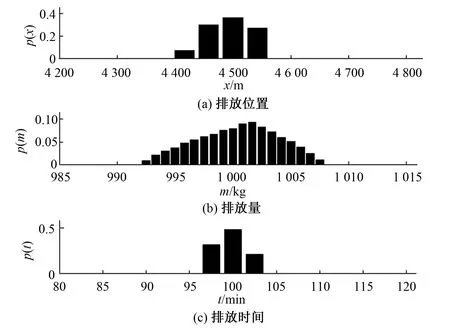
图3 GIBBS抽样结果Fig.3 GIBBS sampling results

2.2 溯源效果分析

为进一步分析对比两种抽样方法的溯源效果，对两种方法分别进行了以下操作：绘制抽样过程中的迭代曲线(见图4、5)；剔除掉迭代前期不稳定的结果，此次研究中根据实验结果情况剔除掉了前200次迭代的结果，对迭代后期较稳定的数据进行统计分析(见表3)。

表3 M-H与GIBBS方法误差统计表Tab.3 M-H and GIBBS method error statistics

图4 M-H法迭代曲线Fig.4 M-H method iteration curve

图5 Gibbs法迭代曲线Fig.5 Gibbs method iteration curve

通过分析M-H抽样方法与GIBBS抽样方法的抽样结果，迭代曲线以及误差统计表可以得到两种方法各自的优点及其之间的差异性：

(1)M-H抽样方法的计算精度更高。从抽样结果图可以看出，3个待反演的参数都极为接近真实值。但需要的计算时间也更长，这是因为每一次通过建议分布计算的值还要进行接受概率的计算。不难看出，由于接受概率的存在，在数据维度更高的情况下，需要的计算时间会更长。

(2)GIBBS抽样方法的计算精度略低于M-H抽样方法，其抽样得到的待反演参数的分布区间相对较宽。但GIBBS抽样需要的计算时间较短，这是因为GIBBS抽样中没有判断接受概率的环节，故其在高维数据的计算中具有一定的优势。

(3)对迭代情况而言，两种算法的收敛程度均较好，能够较快的在迭代计算中趋近于真实值。

(4)对计算误差而言，两种方法对于3个待反演参数的计算误差都远小于5%，计算精度很高。M-H算法中对于污染物排放位置和排放量的计算结果是相对准确的。

3 结 论

(1)基于MCMC方法的M-H抽样方法和GIBBS抽样方法能够准确地对突发点源岸边污染物瞬时排放事件进行溯源，其计算结果接近于真实值，能够有效地解决点源岸边污染物瞬时排放的溯源问题。

(2)本研究中的创新点为对M-H采样方法做了改进：根据建议分布采样时先判断所取样本值是否使后验概率密度函数有意义，如果无意义则重新根据建议分布采样，再判断接受概率是否满足条件。这样可以有效加快迭代时的收敛速度，使待反演参数的抽样值更快地趋近于目标值。从计算结果可以看出这样的改进是比较有效的。改进的M-H抽样方法在计算精度上要高于GIBBS抽样方法，但由于添加了抽样的判断条件其计算时间也较长。而GIBBS抽样方法在高维数据的处理上具有一定的优势。

(3)通过案例应用, 一方面论证了采用概率方法，即通过对后验概率密度函数抽样从而进行突发水污染溯源的可行性；另一方面也说明本研究采用的改进的M-H抽样方法与传统的GIBBS抽样方法相比在提高计算精度，精确溯源污染源信息方面的优势所在。

□