基于IBA-RBF的水电站厂房结构振动响应预测
刘丹彤,杜志达
(大连理工大学建设工程学部,辽宁 大连 116024)
0 引 言
水电站厂房结构具有支撑发电机组和水体通过的双重作用。随着水电事业的飞速发展,在装机容量日益扩大的同时,由多种因素引发的厂房结构振动问题也日渐突出,威胁着电站的安全运行。目前各大型水电站对机组振动及水流脉动情况已建立了较为完善的监测体系,然而受现场条件限制,较少在厂房结构上布设测点[1]。为全面地掌握和控制电站的运行情况,如何利用有限的监测数据预测厂房结构的振动状态和振动响应成为一项重要课题[2,3]。
在水力、机械、电磁等因素的共同作用下,水电站厂房结构的振动特性呈现典型的高维非线性和多源不确定性特点,为厂房结构振动响应的计算分析带来了不小的挑战[4,5]。由于各类振源的产生机理与作用方式各不相同,其动荷载大小及幅频特性亦难以确定,机组与厂房结构间耦联振动的存在进一步增大了利用有限元及结构动力学方法求解的难度,因此厂房结构的振动问题一直是国内外学术和工程领域的关注重点[6]。许多研究者做了大量的工作,练继建等[7]提出基于BP神经网络的水电站厂房结构振动位移预测模型,结合三峡水电站这一实例验证了模型的适用性。徐国宾等[8]利用SSPSO-GRNN模型对厂顶溢流式水电站厂房结构的振动位移进行预测,获得了在0.004左右波动的均方误差。宋志强等[9]提出了改进的萤火虫算法(IFA),并利用其优化BP神经网络的权值和阈值,提出水电站厂房结构振动加速度预测模型IFA-BPNN。苗宗伟等[10]通过对景洪水电站现场试验数据的分析,证明了厂房结构振动与机组振动间的耦联作用及相关性。练继建等[11]以二滩水电站原型观测数据为基础,利用粒子群算法(PSO)优化最小二乘支持向量机(LS-SVM)的参数,对厂房结构振动响应进行了预测,预测误差在20%以内。以上研究说明了通过机组振动和尾水脉动的监测数据预测厂房结构振动响应的可行性,对于保障水电站的安全经济运行起到了积极作用,但预测精度上的不足,有待于进一步完善。
本文基于对蝙蝠算法寻优策略分析,在全局寻优和局部搜索阶段分别引入动态扰动因子和正切随机探索机制,采用惯性权重递减策略对两种搜索机制进行平衡。以线性变化的方式更新脉冲音量和脉冲频率,同时进行种群刷新操作加快寻优效率。提出改进蝙蝠算法(IBA)并利用其对径向基函数神经网络(RBF)的扩展参数P进行优选,基于机组振动和尾水脉动的监测数据建立水电站厂房结构振动响应预测的IBA-RBF模型,对水电站厂房结构振动响应进行了高精度预测。
1 基本蝙蝠算法及其改进
1.1 基本蝙蝠算法
蝙蝠算法自2010年Yang[12]提出以来,以其收敛快、参数少、通用性强的优势,广泛应用于数据挖掘[13,14]、图像处理[15,16]、模式识别[17]等诸多领域,并取得了较好的效果。但作为一种群体智能优化算法,蝙蝠算法也存在着易陷入局部极值、后期收敛慢的缺陷。通过迭代过程中脉冲音量和脉冲频率的适应性改变,蝙蝠种群实现了全局寻优与局部搜索两部分间的动态转换,具体实现步骤如下:

fi=fmin+(fmax-fmin)×β
(1)

(2)
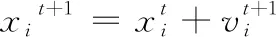
(3)
式中:β是[0,1]上服从均匀分布的随机向量;fmin、fmax分别为种群发射超声波的最小和最大频率。
Step2:局部搜索—接近全局最优解的蝙蝠(以随机生成的均匀分布的随机数rand1为判断阈值,若rand1>第i只蝙蝠的脉冲频率ri)采用以下方式在最优个体附近产生新解xnew:
xnew=xold+εAt
(4)
式中:ε为[-1,1]上均匀分布的随机数;At为第t次迭代时种群脉冲音量的平均值。
在个体发现猎物后,脉冲音量Ai和脉冲频率ri按下式更新:
Ait+1=αAit
(5)
rit+1=ri0[1-exp(-γt)]
(6)
1.2 动态扰动因子
基本蝙蝠算法中蝙蝠个体每次全局搜索时都受上一次迭代时所在位置与当前最优位置间距离的制约,捕食空间有限,易陷入局部最优。借鉴文献[18]的改进思路,引入动态扰动因子δ对上一次迭代时所在位置进行扰动,以提高种群捕食的灵活性。搜索前期扰动力度较大,全局搜索的开拓能力较强,随着捕食过程的进行,δ逐渐减小以保证算法收敛。动态扰动因子δ和改进后的位置更新公式如下:
(7)
(8)
式中:Tmax为最大迭代次数;κ为扰动偏离因子,κ∈[0.1,0.9],经多次试验确定其取值,本文取κ=0.5;betarnd( )为服从贝塔分布的随机数,对自适应减小的δ值进行扰动以提高全局搜索能力。
1.3 惯性权重递减策略
蝙蝠算法和粒子群算法都是耦合个体在解空间的全局搜索与局部搜索实现寻优,可参考粒子群算法中的惯性权重w递减策略平衡两种搜索机制,改进后的速度更新公式如式(11)所示:
c=1/Tmax×ln(wmax/wmin)
(9)
w=wmax-(wmax-wmin)×ect
(10)
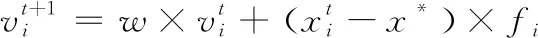
(11)
式中:wmax、wmin分别为惯性权重w的最大值和最小值,本文取wmax=0.9,wmin=0.4。
1.4 正切随机探索机制
针对基本蝙蝠算法在局部搜索阶段以当前最优位置为基准均匀向外探索、局部挖掘能力较弱的缺陷,利用柯西分布函数[19]按下式对局部搜索机制进行改进:
xnew=xold+Attan[π(λ-0.5)]
(12)
1.5 脉冲音量和频率线性渐变
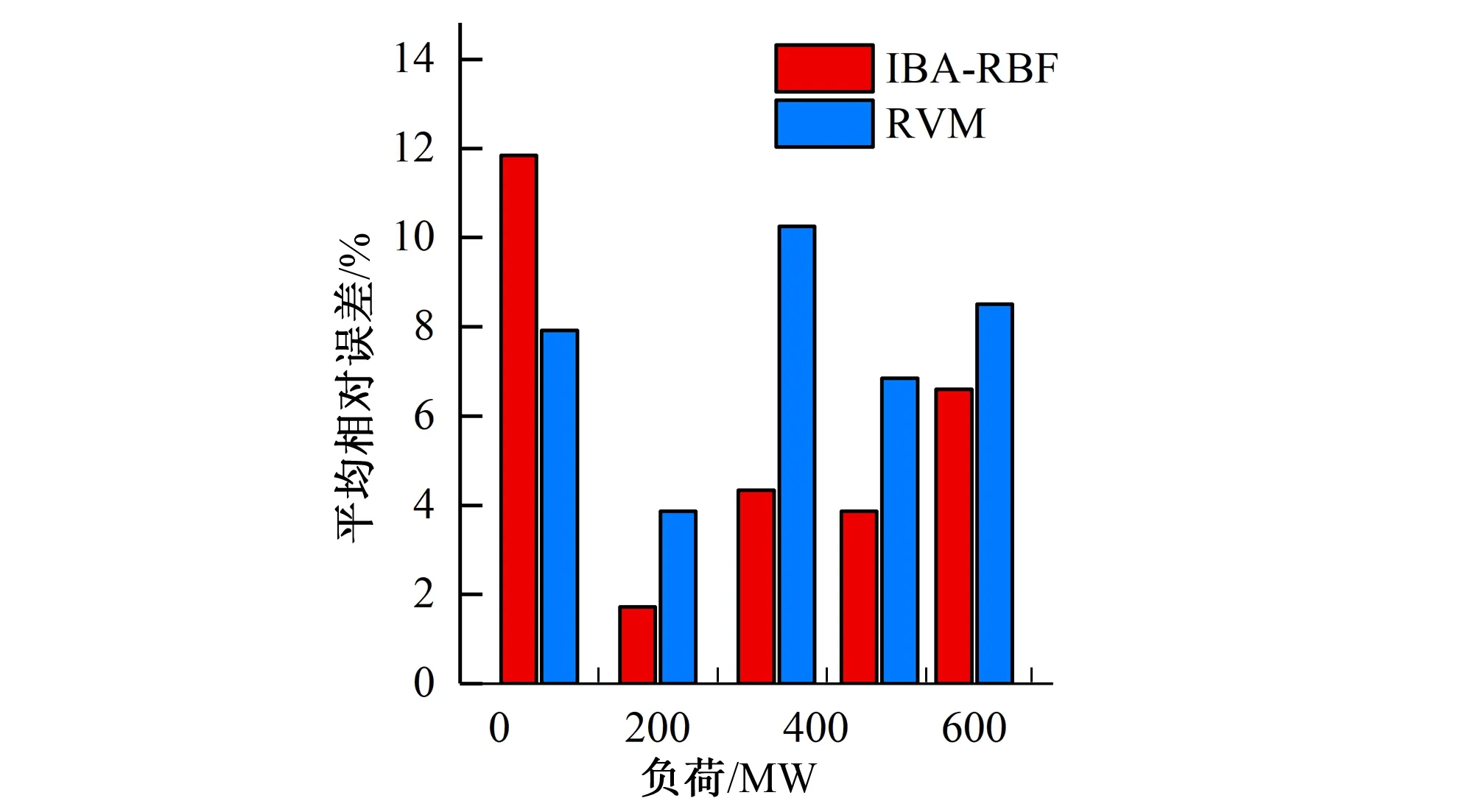
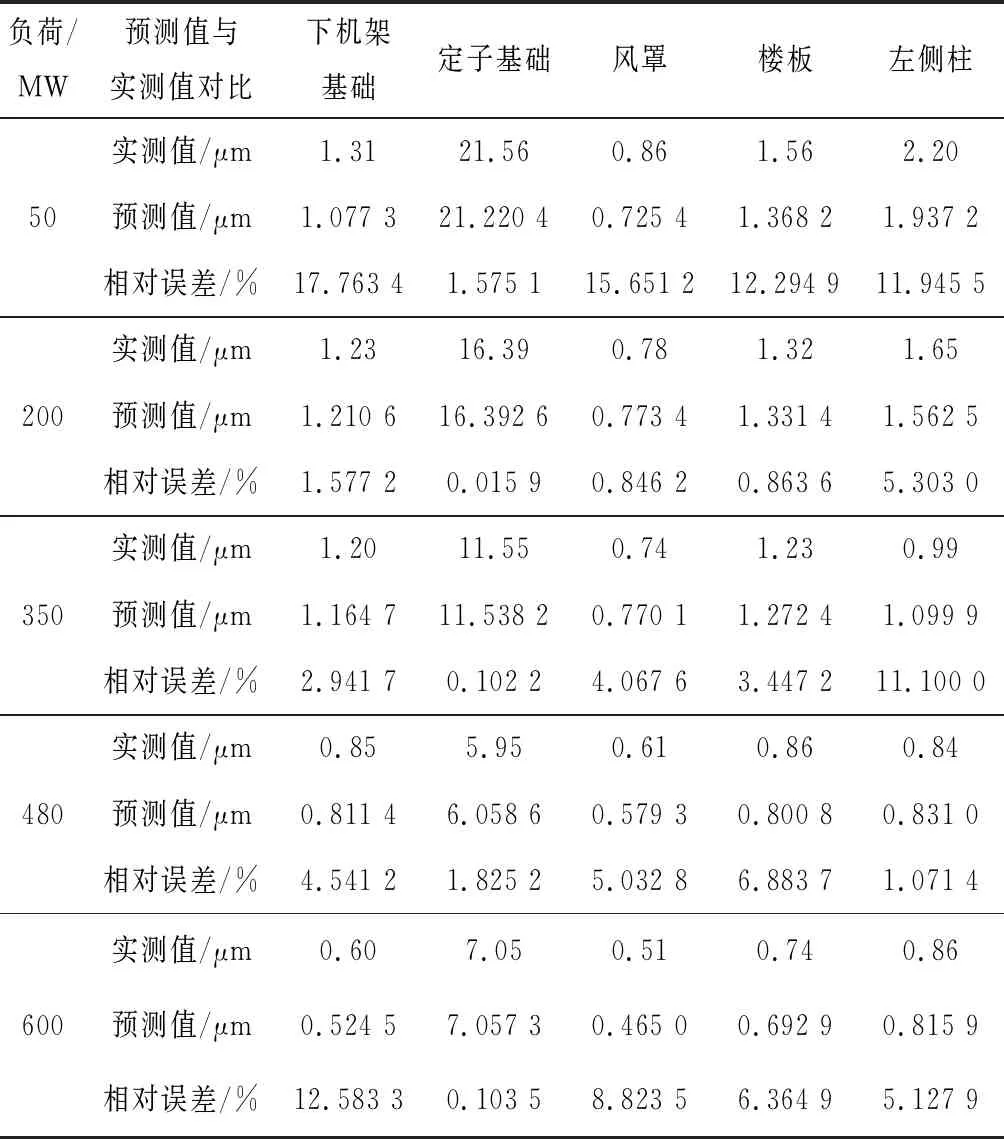
基本蝙蝠算法产生新解的条件为:rand1>ri,接受新解的条件为:新解的适应度优于当前最优解的适应度f(xnew) (13) (14) 式中:Amax、Amin、rmax、rmin分别为整个蝙蝠种群的最大、最小脉冲音量及最大、最小脉冲频率。 借鉴人工免疫算法(Immune Algorithm)的种群刷新策略,每次迭代用随机产生的新个体替换适应度排名后10%的个体,以加快寻优效率。 为比较改进蝙蝠算法(IBA)与基本蝙蝠算法(BA)的寻优性能,以Schaffer、Griewank、Ackley、Sphere 4个典型函数的最小化问题进行测试,测试过程中参数设置如表1所示。 表1 测试过程算法参数设置Tab.1 Test process algorithm parameter settings (1)Schaffer函数。 f(xi)=0.5+ (15) 函数的测试区间为xi∈[-2.048,2.048],在xi=0处取最小值0。 (2)Griewank函数。 (16) 测试区间为xi∈[-600,600],在xi=0处取全局最小值0,该函数是典型的非线性多模态函数,难以找到全局最小值。 (3)Ackley函数。 (17) 函数的测试区间为xi∈[-30,30],在xi=0处取全局最小值0。 (4)Sphere函数。 (18) 函数的测试区间为xi∈[-100,100],该函数是典型的单峰函数,在xi=0处取全局最小值0。 设置测试函数的维数D=10,利用BA、IBA算法分别对上述4个函数最小值问题进行寻优,将每个函数独立运行20次的结果进行统计分析,如表2所示。 表2 函数测试结果Tab.2 Function test results 由表2可知,改进后的蝙蝠算法对于多维的单峰、多峰函数均具有较好的寻优性能和稳定性,与基本蝙蝠算法相比最优精度、最差精度均得到了较大提高,平均精度至少提高了1个数量级。 RBF神经网络于1988年提出[21],以非线性回归理论为基础,结构简单、不受初始权值影响,可以任意精度逼近复杂非线性函数[22],更适合于水电站机组与厂房结构间耦联振动的预测分析。通过调用MATLAB工具箱中的newrbe(·)函数生成一个精确的RBF网络,其格式如下: net=newrbe(input,output,P) (19) 式中:input、output分别为训练样本的输入和输出向量;P为网络的扩展参数,其值的选取对网络性能有较大影响。 为提高网络的预测精度,本文采用IBA优化RBF神经网络的扩展参数,将蝙蝠个体位置编码为RBF网络的扩展参数P,以RBF网络的均方误差MSE为适应度函数,模型计算流程如图1所示。 图1 基于IBA-RBF的水电站厂房结构振动响应预测模型流程图Fig.1 Flow chart of vibration response prediction model for hydropower house based on IBA-RBF 采用文献[23]中的水电站原型观测数据进行分析,利用机组振动和尾水脉动压力数据预测厂房结构的振动响应。以机组顶盖、上、下机架3个部位X、Y、Z三向振动位移及尾水脉动压力10个影响因素95%的双幅值为输入因子,以厂房结构定子基础、下机架基础、楼板、风罩、左侧柱5个测点Z向振动位移标准差为输出因子。为充分检验模型性能,选择与文献[23]相同的训练与测试数据,在训练与测试前,对数据进行归一化处理。 确定模型的输入层神经元数目为10,与厂房结构振动的10个影响因子相对应,输出层神经元数目为5,对应于厂房结构5个测点的振动位移标准差。设置IBA-RBF模型参数如下:蝙蝠种群规模M为50,最大迭代次数Tmax为50,蝙蝠个体频率范围[fmin,fmax]=[0,2],脉冲音量范围[Amin,Amax]=[0,1],脉冲频率范围[rmin,rmax]=[0,0.5],蝙蝠个体位置范围[xmin,xmax]=[10-5,5]。 将5组不同负荷下的测试数据代入已训练好的IBA-RBF模型中进行厂房结构振动响应仿真,预测结果如表3所示,并与文献[23]中的RVM模型进行对比见图2,绘制各负荷下5个测点振动响应预测结果的平均相对误差如图3所示。 表3 厂房结构振动响应预测结果Tab.3 Prediction results of vibration response of hydropower house structure 由表3、图2可以看出,IBA-RBF模型预测精度较高,除以负荷50 MW工况为测试数据误差略大外,200、350、480、600 MW负荷下模型的预测效果均优于RVM模型的预测效果,与实测值非常接近。由表3、图3可知,IBA-RBF模型对于厂房结构各测点、各工况的预测误差大多位于5%以下,5组负荷下的平均相对误差为5.6741%。而文献[23]所提出的相关向量机(RVM)模型预测的相对误差大多位于8%以下,平均相对误差为7.476 5%。与RVM模型相比,IBA-RBF模型的泛化能力有较大提升,更适用于水电站厂房结构振动响应的高维非线性预测。 本文在基本蝙蝠算法的基础上,对蝙蝠种群的全局寻优、局部搜索以及脉冲音量和脉冲频率的更新机制进行改进,同时引入惯性权重递减和种群刷新策略,提出改进蝙蝠算法IBA。并利用该算法优化RBF网络的扩展参数P,基于机组振动和尾水脉动的监测数据建立水电站厂房结构振动响应预测的IBA-RBF模型,主要结论如下。 图2 各测点振动位移实测值与预测值对比Fig. 2 Comparison of measured and predicted values of vibration displacement of each measuring point 图3 不同工况下平均相对误差对比Fig.3 Comparison of average relative error under different working conditions (1)改进后的蝙蝠算法一定程度上弥补了基本蝙蝠算法易陷入局部极值的不足,与基本蝙蝠算法相比最优精度、最差精度、平均精度均得到了较大提高,对于多维的单峰及多峰函数都具有较好的寻优性能。 (2)与RVM模型相比,IBA-RBF模型预测精度和泛化能力得到了显著提高,可为水电站厂房结构振动响应监测与控制提供一种新方法,为电站的安全运行提供一定技术保障。 □
1.6 种群刷新
2 函数测试


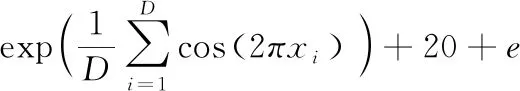


3 基于IBA-RBF的水电站厂房结构振动响应预测模型

4 仿真实例分析
4.1 数据来源
4.2 模型的创建与训练
4.3 模型验证与误差分析
5 结 语