基于VMD-LSSVM的月径流预测方法研究

吕晗芳，赵雪花，桑宇婷，祝雪萍，张丽娟

(太原理工大学水利科学与工程学院，太原 030024)

0 引 言

径流预测是水资源管理、调度和高效利用的基础[1]。径流过程是一个涉及水文、气象及力学等的复杂过程，既受确定性因素的作用又受随机因素的影响[2]，并呈现出非线性、非平稳性的特点。随着计算机技术和数学算法的不断发展，涌现出了一大批与机器学习和人工智能方法结合的研究。Suykens在传统支持向量机(Support Vector Machines，SVM)的目标函数中引入误差平方和项，并提出最小二乘支持向量机(Least-Square Support Vector Machines，LSSVM)方法，该方法收敛精度高，具有较好的非线性拟合能力[3,4]。目前最小二乘支持向量机在信号处理和时间序列预测等领域得到了广泛应用，周秀平[5]将LSSVM-马尔科夫链组合模型成功应用于年径流预测；张楠[6]利用最小二乘支持向量方法，构建了基于多因子量化指标的径流预测模型。

然而，仅用一个预测方法建立的预报模型很难反映水流序列的变化机制，这样的单一模型会丢失隐含在原始序列中的重要信息。有研究指出，径流时间序列的预处理对于提高预测精度是十分必要的。因此，当前提高精度的关键在于对数据的预处理，充分挖掘有限样本包含的信息，并提取反映其变化规律的成分，再对这些成分建立模型，进而形成组合预测的建模思路以提高预测精度[7]。

小波分析、经验模态分解(Empirical Mode Decomposition，EMD)和完备总体经验模态分解法(Complete Ensemble Empirical Mode Decomposition with adaptive noise，CEEMDAN)是基于信号分析的分解方法，已常见于径流数据的预处理阶段。小波分析具有良好的时频局域化特性，但自适应差且受人为因素影响较大；EMD自适应强，却存在端点效应和过包络等问题；CEEMDAN减小了白噪声引起的误差，但分解后会存在虚假模态，影响算法的精确度[8-11]。为了解决上述分解方法出现的问题，Dragomiretskiy[12]提出了是一种新的信号分解方法----变模态分解(Variational Mode Decomposition，VMD)[13-14]。相比EMD的递归筛选模式，VMD是一种完全非递归的变分模态分解，具有坚实的理论基础，表现出更好的噪声鲁棒性。本文采用VMD对汾河上游月径流数据进行预处理，分解出一系列含有单一频率信息的分量，再对这些分量建立LSSVM预测模型，最后重构预测分量得到径流预测结果，并对结果进行分析以验证该方法的有效性。

1 模型与方法

1.1 变分模态分解(VMD)

VMD的目标是将原始信号分解为一系列具有特殊稀疏性的离散模态分量，该方法能够自适应地确定相关波段并同时计算各模态分量，并更好的平衡解决各部分存在的噪声。构造变分模型和求模型最优解的主要步骤如下：

(1)对模态函数进行Hilbert(希尔伯特)变换，并在得到的单侧频谱中加入各模态的中心频率，使得解析信号转换为其对应的基频带信号。计算该信号的梯度平方L2范数，并定义它为各模态分量的带宽，此时VMD模型转化为约束变分问题。

(1)

式中：x为径流序列；uk为模态分量；ωk为模态的中心频率；k为模态分量数；t为时间变量。

(2)在求解模型时，引入二次惩罚函数项和拉格朗日乘子算子，将上述约束变分问题转化为非约束变分问题，并运用乘子交替方向法求解模型计算最优解。

L({uk},{ωk},λ)=

(2)

(3)最终，各模态分量解得，

(3)

式中：λ为拉格朗日乘子；α为二次惩罚系数；i和k为模态分量数。

(4)根据式(3)不断更新ukωkλ，直到满足约束条件：

(4)

式中：ε为预先设置的极小值实数，本文取值10-7。

1.2 最小二乘支持向量机(LSSVM)

最小二乘支持向量机(LSSVM)是对支持向量机(SVM)的改进，其代替传统二次规划方法解决函数估计问题，引入最小二乘线性系统到支持向量机中，具体步骤如下：

(1)对于给定训练样本集{xi,yi}，其中i=1,2,…,N，xi为输入数据，yi为输出数据，应用核函数将样本转换到高维空间中，则样本满足线性规律：

f(x)=βTφ(x)+b

(5)

式中：βT为高维空间超平面的法向量；b为偏置量；φ(x)为非线性映射函数。

(2)依据结构风险最小化原理，将回归问题转化成一个等式约束的优化问题：

(6)

式中：ei为误差；γ为正则化参数。

(3)针对目标函数建立拉格朗日等式：

(7)

式中：θ为拉格朗日乘子。

1.3 VMD-LSSVM预测模型

由于VMD处理复杂信号的突出优势，本文尝试建立VMD-LSSVM组合预测模型以提高复杂径流序列预测的精度，其模型结构如图1所示。具体模型计算步骤如下：

(1)各站点的月径流时间序列总长516，首先经过EMD、CEEMDAN和VMD分解，可得到一系列具有单一频率信号的固有模态函数(IMF)，即为图中IMF1,IMF2,…,IMFn，VMD法的分解个数设定与CEEMDAN的分解个数相同，选择二次惩罚系数为2 000，噪声容忍度为0。

(2)将一系列IMF分别输入LSSVM中，使用网格搜索进行最优调参并加入归一化提高拟合度，得到各IMF对应的输出值序列，即为图中Y1,Y2,…,Yn。

(3)各输出值重构为最终的预测径流序列。

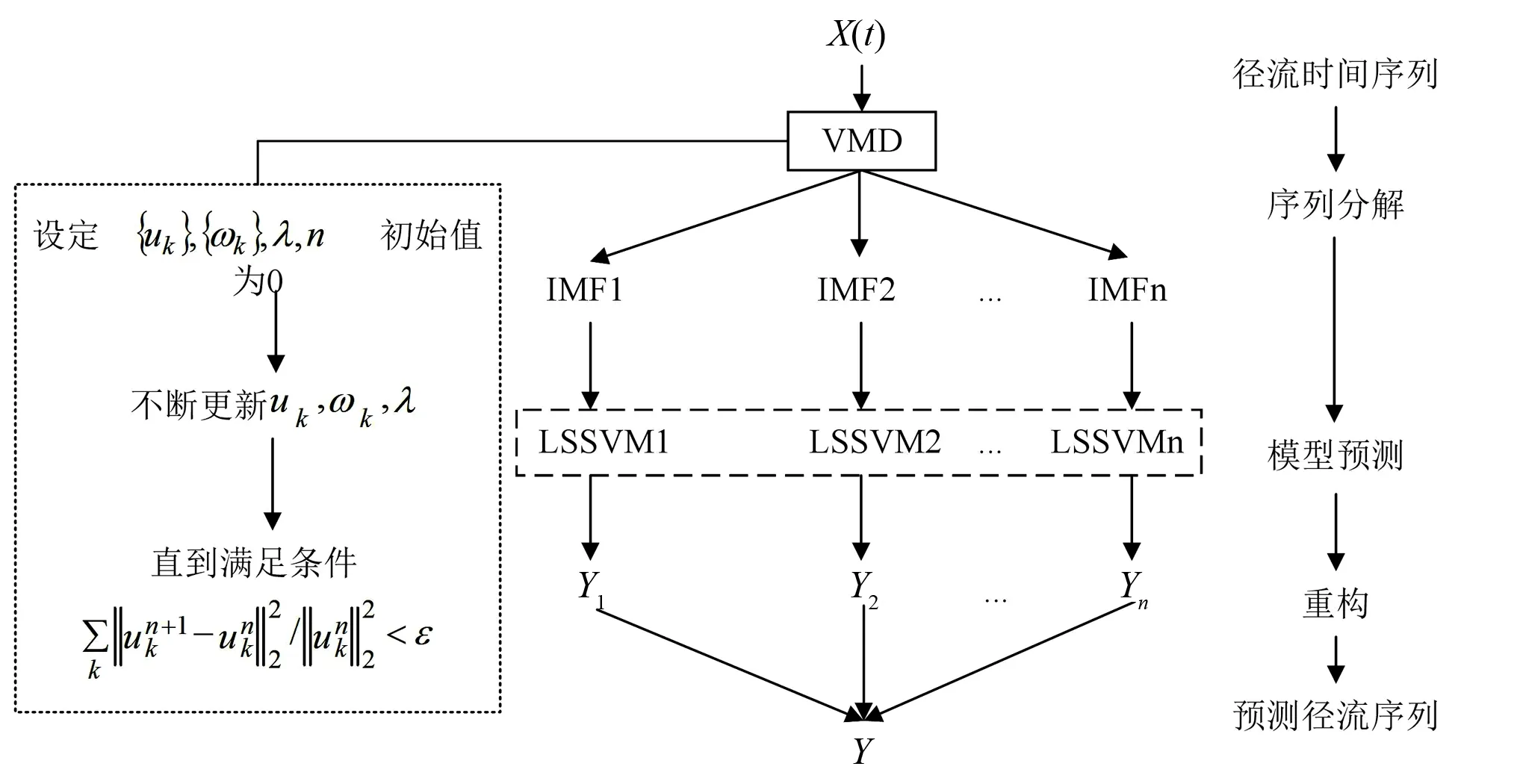
图1 VMD-LSSVM模型预测流程图Fig.1 Flowchart of the VMD-LSSVM model proposed

2 实例分析

汾河作为山西的母亲河，是黄河的第二大支流，位于黄河的中游段，流域面积达38 728 km2。汾河的上游段从宁武县的管涔山河源到太原北郊的兰村，是太原重要的水源地和最大的饮用水功能区，本文研究的4个水文站点均位于汾河上游。上静游站位于汾河支流岚河上，此站上游控制面积为1 140 km2；汾河水库站处于岚河与汾河的交汇处；寨上站坐落于古交市寨上村，控制面积约1 500 km2；兰村站在汾河的中上游，位于太原市西北22.5 km的上兰村。4个水文站1958-2000年月径流数据资料来自山西省水文局，已被运用于多个科研项目及工程，因此可以保证可靠性；且该径流序列较长，资料精度较高，具有很好的代表性，能够客观反映汾河上游径流演变特征。

2.1 月径流资料VMD分解

利用VMD法对4个水文站的月径流资料进行分解，各站原始径流序列和其分解IMF分量的频谱图如图2所示。原始径流数据包含多频率的径流序列信息，呈现“杂乱无章”的特点，很难找到其中蕴含的变化规律。随着频率的增大，原始径流序列的幅值变化出现多个峰值，代表在某段频率周期中径流序列出现了大幅度变化，相较其他的小幅变化这种变化能够主导序列的趋势，这类峰值变化信息为主要频率信息，包含主要频率信息的分量为主要频率分量。而VMD法分解出的各IMF分量能够将原始序列的多个频率分解开来，并且这些预处理后的分量能够自适应的提取重要变化信息。兰村站的IMF1、IMF3、IMF4、IMF6与其他站点的IMF1、IMF2、IMF4、IMF6分别包含了各主要频率信息，剩余的IMF包含其他相关信息。各IMF分量在主要频率信息的其余各处幅值基本为0，说明VMD可以在不影响重要信息的情况下自适应地去除不利于模型预测的噪声，在分解与提取的同时体现了优秀的除噪效果，更突出了重要变化信息，使得原始数据变化过程易于读取。

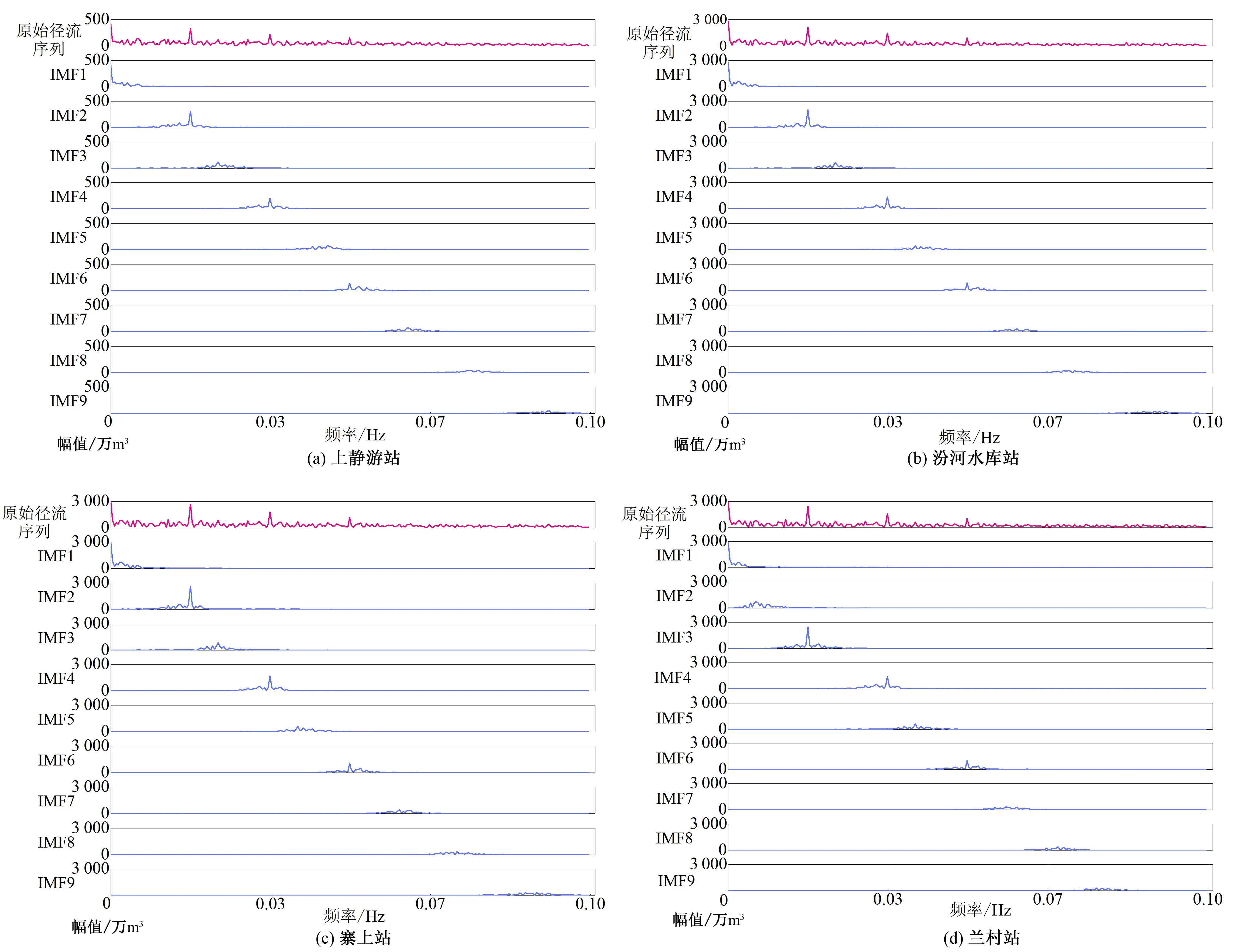
图2 月径流序列的VMD分解结果图Fig.2 VMD decomposition results of monthly runoff series

2.2 预测结果分析

本文使用上静游站、汾河水库站、寨上站和兰村站1958-2000年总计516个月径流资料，其中前492个数据即1958年1月至1998年12月径流资料为训练集，这组数据用于模型模拟及训练，后24个数据即1999年1月至2000年12月径流资料为测试集用于测试模型预测效果。

为对比模型预测效果，本文选择4种模型进行分别预测，包括单一预测LSSVM模型、组合预测EMD-LSSVM模型、CEEMDAN-LSSVM模型以及VMD-LSSVM模型。各模型预测结果与原径流数据的对比见图3。

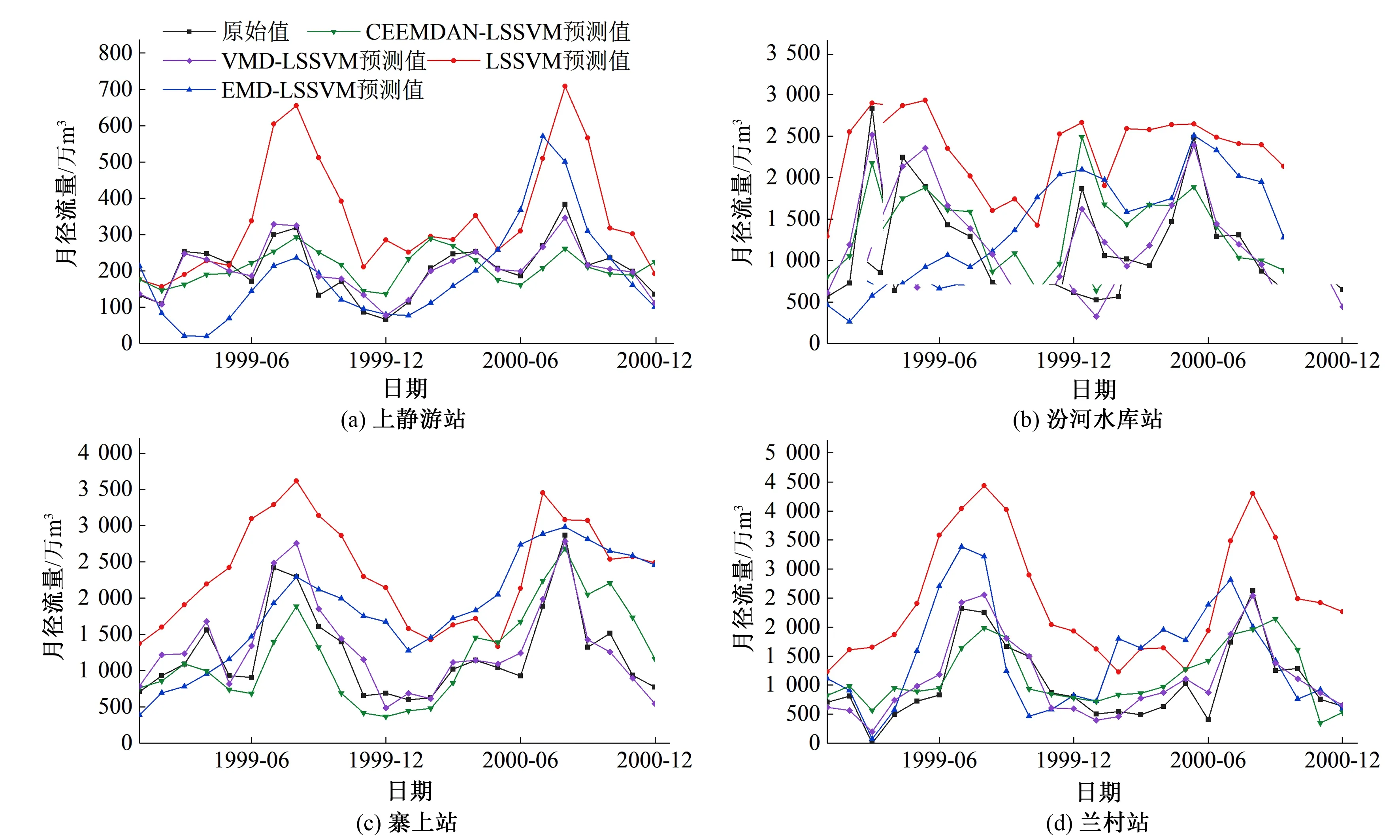
图3 4个水文站各模型预测结果对比图Fig.3 Forecast results by using each model at four hydrological stations

由图3可知：①在单一LSSVM预测模型下，4个站点的预测效果并不理想，只能够显示出大致的变化趋势，并且大部分预测数据比实测数据高60%左右，在4种模型中预测效果最差。其中最为明显的是，上静游站1999年6-10月与2000年7-9月预测值明显远大于实测值。②组合模型EMD-LSSVM的预测效果相较单一预测模型更好，更接近实测值，但仍有部分数据存在趋势相反或误差大于50%的情况。③在使用组合模型CEEMDAN-LSSVM时，预测结果的变化趋势已基本与实测序列相同，误差相较EMD-LSSVM模型减少了约40%，在4个模型中预测效果仅次于VMD-LSSVM模型，仅有个别数据存在误差较大的情况。这说明CEEMDAN比EMD减少了模态混叠的现象，使预测效果得到提高。④组合模型VMD-LSSVM的预测效果与实测径流曲线拟合度最好，变化趋势与原序列相同，且无极端值出现，可以初步判断，VMD分解方法较经验模态系列方法能更好地应对序列中包含的复杂频率信息，且与LSSVM组合应用效果更好。

为了更清晰地阐述模型预测效果，平均绝对误差MAE、均方根误差RMSE、平均绝对百分比误差MAPE和纳什效率系数NS4个指标将用于分析预测精度，计算公式如下：

(8)

(9)

(10)

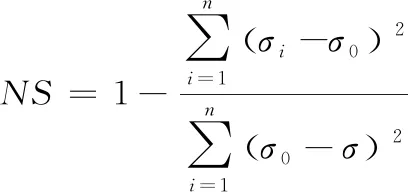
(11)

式中：σi为i时刻的预测值；σ0为i时刻的实测值；σ为实测值的均值。

根据《水文情报预报规范(GB/T 22482-2008)》的规定，当NS≥0.90时，预测精度为甲级；0.70≤NS<0.90时，预测精度为乙级；0.50≤NS<0.70时，预测精度为丙级。

表1为汾河上游4个水文站的精度指标结果，从中可以分析得到：①各模型在训练期的NS指标为0.7以上，达到丙级以上水平，且随着模型的优化，从单一预测模型到组合预测模型，从应用递归的经验模态系列方法到应用非递归、分解更完全的变分模态分解方法，MAE、MAPE和RMSE指标逐渐减小，NS逐渐靠近1。②测试期预测结果关于模型的比较更加明显，VMD-LSSVM模型的MAE、MAPE和RMSE与单一LSSVM模型相比分别减少了80%～90%、75%～90%、50%～90%；与EMD-LSSVM模型相比分别减少了70%～80%、60%～85%、50%～80%；与CEEMDAN-LSSVM模型相比分别减少了50%～75%、40%～70%、40%～70%。VMD-LSSVM模型的NS为0.81～0.92，预测精度为甲级；EMD-LSSVM模型的NS为0.50～0.68；CEEMDAN-LSSVM模型的NS为0.69～0.83；LSSVM模型的NS为0.21～0.31，预测结果不可信。③训练期整体比测试期预测效果要好，各模型都存在不同程度的过学习现象。以寨上站为例，LSSVM模型测试期RMSE为训练期的近10倍，而VMD-LSSVM模型测试期RMSE为训练期的3倍。LSSVM单一模型对训练样本内的噪声和孤立点比较敏感，由于径流序列的复杂多频特性，其含有的不利噪声表现为频谱图中各个频率段掺杂的无序低幅值波动，这会影响LSSVM的回归拟合，而VMD分解能够使复杂信息转化为主要频率信息和其他信息，并且有优秀除噪效果，有利于LSSVM寻找最优回归参数以降低输出误差，所以将分解后的IMF分量再输入LSSVM进行预测能够减少噪声对模型预测精度的影响。④整体来看，上静游站和兰村站的VMD-LSSVM模型预测效果最为理想，NS达到甲级，而汾河水库站与寨上站的预测精度最高只能达到乙级。

表1 4个水文站各模型预测误差对比Tab.1 Prediction error of each model at four hydrological stations

表2 4个水文站两类分量的预测误差及权重对比Tab.2 Prediction error and weight of each types of components at four hydrological stations

为了更加深刻地描述VMD分解方法在预测中的应用效果，做出4个水文站两类分量的预测误差及权重对比(见表2)。通过VMD法分解后可以得到各站的IMF分量，提取出各站的主要频率分量与其他频率分量，对这组原始数据与预测数据进行NS误差分析，并计算两类分量的线性权重。主要频率分量的NS接近1，预测精度高，而其他频率分量精度稍低，并且主要频率分量较其他频率分量在预测序列中权重大，说明主要频率分量在预测中有重要地位，该分量精度的提升可以带动总体VMD-LSSVM模型精度的提高，研究这类信息的提取和预测对于提高整体预测精度具有重要意义，这也表明了VMD-LSSVM组合模型对于月径流序列预测的优势所在。

综上所述，汾河上游径流序列的预测效果优劣排序应如下：VMD-LSSVM > CEEMDAN-LSSVM > EMD-LSSVM > LSSVM，组合模型较单一预测模型在预测精度上有一定的优势，其中VMD-LSSVM模型相较EMD-LSSVM和CEEMDAN-LSSVM在训练期和测试期都能达到较高精度，该模型用于复杂多频信息的径流序列预测是可行、有效的。

3 结 语

(1)在对复杂的径流序列进行预测时，单一LSSVM模型的预测结果不可信，需要将序列进行预处理后再预测，经过分解后进行预测再重构的组合模型法可以大幅提高预测精度。

(2)相比经验模态系列方法的递归筛选模式，变模态分解法是一种完全非递归的变分模态分解，具有坚实的理论基础，能够提取出主要频率信息，表现出更好的噪声鲁棒性，从而有利影响预测效果，进一步提高预测精度。

(3)VMD-LSSVM模型首先将实测径流数据分解为一系列子序列，并提取出主要频率分量和其他相关信息，再把该组序列分别输入LSSVM进行预测，得到对应的一组预测序列，经重构后为最终的预测数据。该方法的预测效果与EMD-LSSVM、CEEMDAN-LSSVM和LSSVM相比误差最小，NS为乙级以上。VMD-LSSVM模型用于包含多频率信息的复杂径流序列预测是可行且有效的，该模型可以推广到与汾河上游地理环境相似的流域。

□