基于改进布谷鸟搜索算法优化的SVM月径流预测
李 代 华
(云南省水文水资源局文山分局,云南 文山 663000)
1 研究背景
环境变化及人类活动加剧给径流的精准预报带来了新的挑战,积极探索具有较好预报精度的模型及方法一直是水文预报研究中的热点和难点问题。支持向量机(Support Vector Machines,SVM)是Vapnik等人提出的一种新型通用学习方法,能较好地解决小样本、非线性、高维数和局部极小点等实际问题,已在水文预测预报[1-3]及枯水期月径流预测[4-6]中得到应用。研究表明,SVM核函数等关键参数的合理选取是提高SVM预测精度的关键。目前,除试错法、网格搜索法选取SVM相关参数外,智能算法常被用于SVM关键参数的选取,包括遗传算法[3](genetic algorithm,GA)、粒子群优化(particle swarm optimization,PSO)算法[4]、人工鱼群算法[5](artificial fish swarm algorithm,AFSA)、果蝇优化算法[7](fruit optimization algorithm,FOA)、布谷鸟搜寻(Cuckoo Search,CS)算法[8]、灰狼优化(gray wolf optimization,GWO)算法[9]、文化算法[10](cultural algorithm,CA)、SCE-UA算法[11]、混合蛙跳算法[12](shuffled frog leaping algorithm,SFLA)、入侵杂草优化(invasive weed optimization,IWO)算法[13]、帝国竞争算法[14](imperialist competitive algorithm,ICA)、人工蜂群优化(artificial bee colony,ABC)算法[15]等。然而,在实际应用中,智能算法优化SVM关键参数存在以下两方面的不足:①传统GA、PSO、CS等标准算法在寻优过程中存在早熟收敛和易陷入局部极值等问题,难以获得SVM“最佳”关键参数。②SVM关键参数中交叉验证参数V对于SVM性能有着重要影响, 取值“小”易导致SVM“欠拟合”,训练样本拟合度低;V取值“大”则易导致“过拟合”,使SVM外推能力差、预测精度低。目前大多数SVM参数优化仅针对惩罚因子C和核函数参数g进行优化,部分增加不敏感系数ε的优化,而对于交叉验证参数V普遍采用试算的方式选取,耗时费力,而且不能保证最优。
基于上述原因分析,为有效提高SVM在水文预测预报中的精度,本文分别提出基于Mittag-Leffler、Pareto、Cauchy 3种重尾分布改进的布谷鸟搜索算法(mittag lefflercuckoo search,MLCS;paretocuckoo search,PCS;cauchycuckoo search,CCS)优化的支持向量机(SVM)月径流预测模型。内容安排如下:①提出MLCS,PCS、CCS 3种CS改进算法,选取6个标准测试函数对MLCS,PCS、CCS算法进行仿真验证,并与标准CS算法的仿真结果进行比较。②利用MLCS,PCS、CCS算法优化SVM交叉验证参数V、惩罚因子C、核函数参数g和不敏感系数ε,构建MLCS-SVM、PCS-SVM和CCS-SVM预测模型,并构建CS-SVM模型作对比,将此4种模型应用于云南省姑老河站枯水期月径流预测研究,旨在验证基于4参数优化的MLCS-SVM、PCS-SVM、CCS-SVM模型用于枯水期月径流预测的可行性和有效性。
2 MLCS-SVM、PCS-SVM和CCS-SVM预测模型
2.1 布谷鸟搜索算法
布谷鸟搜索算法(CS)又名杜鹃搜索算法,其通过模拟布谷鸟寄生育雏来有效求解最优化问题,目前已在各行业领域得到广泛应用。算法需设定3个假设条件:①布谷鸟随机选择1个鸟巢孵化,且1次只产1颗蛋。②最好的鸟巢将会被保留到下一代。③可用鸟巢的数量n是固定的,鸟巢中外来蛋被发现的概率是p0∈[0,1][16]。
在这3个理想状态下,鸟巢位置的更新公式为:
(1)


(2)

2.2 不同重尾改进布谷鸟搜索算法
标准布谷鸟搜索(CS)算法的全局随机游走主要基于L'evy分布来实现,由于 L'evy分布属较简单的一种重尾分布,虽然能使CS算法获得较好的随机性,但也存在遍历性的不足从而导致CS算法种群多样性和全局搜索能力弱。为进一步提高CS算法的群多样性和全局搜索能力,本文提出基于Mittag-Leffler、Pareto、Cauchy 3种重尾分布改进的CS(即MLCS,PCS、CCS)算法[17,18]。
(1)MLCS算法。如果一个随机变量的分布函数满足式(3),则称该随机变量服从Mittag-Leffler分布:
(3)
式中:0<β≤1,x> 0,且对于x≤0,Fβ(x)= 0;对于0<β<1,Mittag-Leffler分布为指数的重尾推广,并且当β=1时减少到指数分布。
参考文献[17,18]提出的方法生成Mittag-Leffler随机数:
(4)
式中:γ表示尺度参数;u、v∈(0,1),表示独立的均匀随机数;τβ为Mittag-Leffler随机数。
基于Mittag-Leffler重尾概率分布,式(1)可以写成:
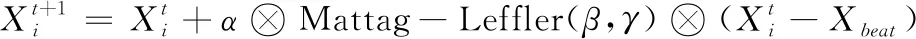
(5)
式中:Mattag-Leffler(β,γ)表示从Mittag-Leffler分布中得出的随机数,本文β=0.8,γ=4.5;其他参数同上。
(2)PCS算法。如果随机变量的累积分布函数满足式(6),则称其服从Pareto(帕累托)分布:
(6)
式中:b>0表示比例参数;a>0表示形状参数(Pareto不等式指数)。
基于Pareto重尾概率分布,式(1)可以写成:
(7)
式中:Pareto(b,a)表示从Pareto分布中得出的随机数,本文a=1.5,b=4.5;其他参数同上。
(3)CCS算法。如果随机变量的累积分布函数满足式(8)具有以下表达式,则称其服从Cauchy分布:
(8)
式中:μ表示位置参数;σ表示比例参数。
基于Cauchy重尾概率分布,式(1)可以写成:
(9)
式中:Cauchy(μ,σ)表示从Cauchy分布中得出的随机数,本文σ=4.5,μ=0.8;其他参数同上。
2.3 支持向量机
SVM通过将低维样本空间映射到高维特征空间,并在高维特征空间中建立线性学习机求解,其学习过程转换为凸优化问题[1-3,8]如下:
(10)
最终回归函数为:
(11)
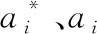
2.4 仿真验证
为验证MLCS,PCS和CCS算法寻优能力,利用MLCS,PCS、CCS对Sphere、Schwefel 2.22、Schwefel 2.21、Schwefel 1.2、Griewank、Ackley 6个典型测试函数进行仿真验证,并与标准CS算法的仿真结果进行比较。6个函数优化维度为30维,最优解为0。其中函数Sphere、Schwefel 2.22、Schwefel 2.21、Schwefel 1.2为单峰函数,主要用于测试算法的寻优精度和局部搜索能力;函数Griewank、Ackley为多峰函数,主要用于测试算法逃逸极部极值能力和全局搜索能力。4种算法重复20次寻优,采用平均值、标准差进行性能评价,见表1;4种算法最大迭代次数T=5 000,鸟巢数量n=50,发现概率Pa=0.25。其中MLCS 算法Mittag-Leffler分布参数β=0.8,γ=4.5;PCS算法Pareto分布参数a=1.5,b=4.5;CCS算法Cauchy分布参数σ=4.5,μ=0.8。其他参数采用各算法默认值。
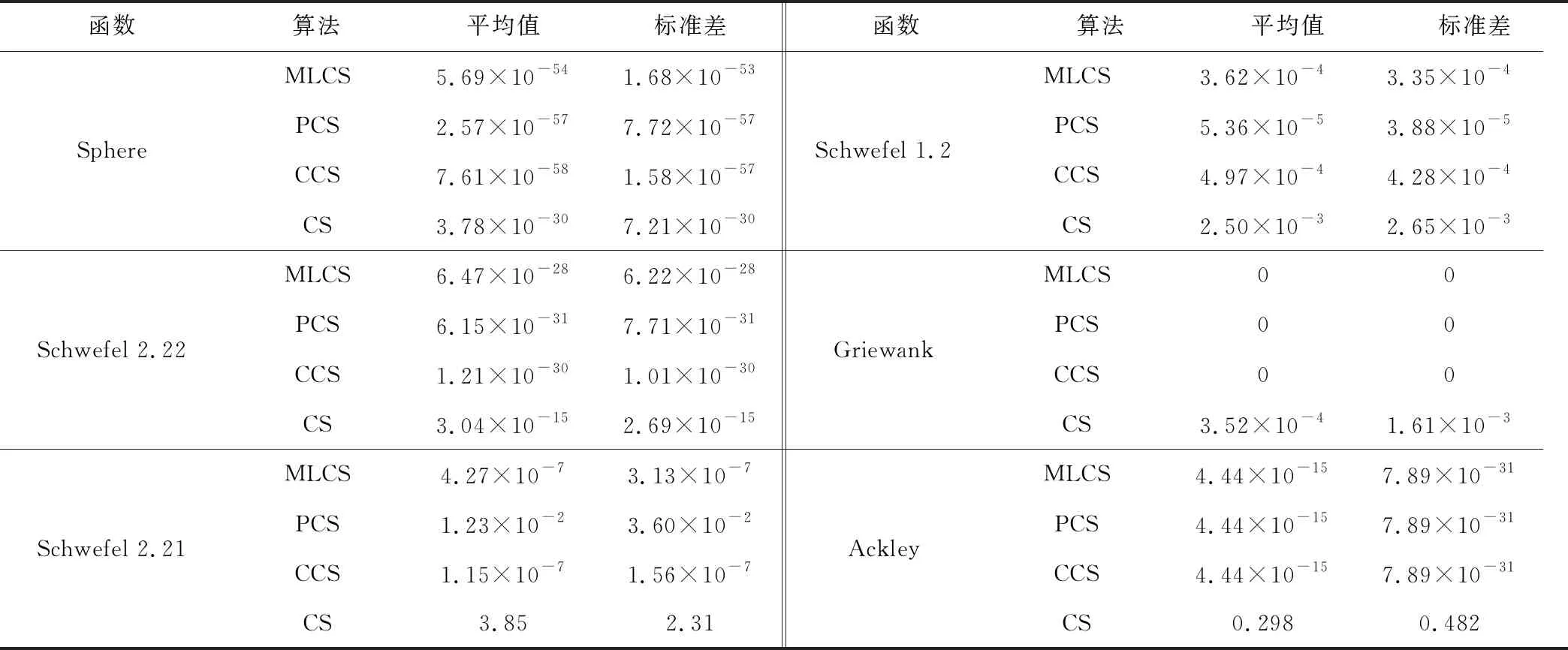
表1 函数优化对比结果
对单峰函数Sphere,MLCS,PCS和CCS算法寻优能力相差不大,CCS算法表现相对较好,3种改进算法寻优精度均高于标准CS算法23个量级以上;对于具有明显转折点的非线性函数Schwefel 2.22,MLCS,PCS和CCS算法寻优能力相似,PCS算法表现相对较好,3种改进算法寻优精度均高于标准CS算法12个量级以上;对于倒锥形非线性函数Schwefel 2.21,CCS、MLCS算法寻优精度略优于PCS算法,优于标准CS算法;对于最优解周围存在很小下降梯度函数Schwefel 1.2,PCS、MLCS、CCS算法寻优效果相差不大,寻优精度优于标准CS算法;对于典型多峰多模态函数Griewank,MLCS,PCS和CCS算法20次寻优均获得了理论最优值0,全局搜索能力远优于标准CS算法;对于连续旋转不可分多峰函数Ackley,MLCS,PCS和CCS算法寻优精度相同,3种改进算法寻优精度均高于标准CS算法13个量级以上。可见,基于Mittag-Leffler、Pareto、Cauchy 3种重尾分布改进的CS算法能有效增强其种群多样性和全局搜索能力,3种改进算法在这 6个函数上的搜索效果均优于标准CS算法,具有较好的寻优精度和全局搜索能力。
2.5 MLCS-SVM、PCS-SVM和CCS-SVM预测实现步骤
步骤1:利用下式归一化处理实测数据,并合理划分训练、预测样本。设置SVM交叉验证参数V和惩罚因子C、核函数参数g、不敏感系数ε的搜寻范围。(由于交叉验证参数V取值为正整数,因此采用fix函数取正)。
(12)

步骤2:确定训练样本均方误差为适应度函数:
(13)

步骤3:随机初始化鸟巢位置,设置鸟巢数量n,最大迭代次数T,发现概率Pa,Mittag-Leffler分布参数β,γ,Pareto分布参数a,b,Cauchy分布参数σ,μ。
步骤4:通过适应度函数计算找出当代最优鸟巢位置Xbest。判断算法是否满足终止条件,若满足,算法结束;若否,执行步骤5。
步骤5:分别执行Mittag-Leffler、Pareto、Cauchy飞行操作,随机产生鸟巢位置。采用式(5)、式(7)、式(9)更新鸟巢位置。计算更新后鸟巢位置的适应度,并与原鸟巢的适应度作比较,若优于原鸟巢则代替原鸟巢,否则丢弃。

步骤7:利用新更新的鸟巢位置计算适应度值,并与前代鸟巢位置对应的适应度值进行比较,保留适应度值更好的鸟巢位置。
步骤8:判断终止条件,若是,输出最优解Xbest;否则重复步骤5~步骤8。
步骤9:利用MLCS、PCS和CCS算法优化获得的交叉验证参数V、惩罚因子C、核函数参数g、不敏感系数ε代入MLCS-SVM、PCS-SVM和CCS-SVM模型进行预测分析。
3 应用实例
(1)数据来源及分析。应用实例数据来源于云南省姑老河站1960-2013年共54年的实测资料。该站1960-2012年上年度月径流与次年枯水期1-3月月径流相关关系见表2。

表2 上年度1-12月月均流量与次年1-3月月相关系数
从表2来看,该站上年度月径流与次年1-3月月径流存在较好的相关性。其中,次年1月月径流与上年度1-12月径流相关系数在0.095~0.938之间;次年2月月径流与上年度1-12月、次年1月月径流相关系数在0.087~0.833之间;次年3月月径流与上年度1-12月、次年1-2月月径流相关系数在0.063~0.794之间。本文选取相关系数较大的上年度8-12月月径流预测次年枯水期1月均径流,选取相关系数较大的上年度9-12月及次年1月月径流预测次年枯水期2月月均径流,选取相关系数较大的上年度9-12月及次年1-2月月径流预测次年枯水期3月月均径流量,并利用前40组实测数据作为训练样本,后13组实测数据作为预测检验样本。
(2)参数设置。MLCS、PCS、CCS和标准CS 4种算法除最大迭代次数 设置为200外,其余参数设置同上。SVM模型相关参数搜索范围:交叉验证参数V∈[2,10]、惩罚因子C∈[0.01,1 000]、核函数参数g∈[0.01,1 000]、不敏感系数ε∈[0.000 1,1]。
(3)模型构建及预测。建立MLCS-SVM、PCS-SVM、CCS-SVM和CS-SVM 4种模型对实例1-3月月径流进行训练及预测,结果见表3;并给出4种模型1-3月训练样本进化过程图和训练-预测相对误差效果图,分别见图1、图2。并利用平均相对误差MRE(%)、最大相对误差maxRE(%)和适应度值对各模型预测性能进行评价。

表3 实例1-3月月径流训练-预测结果及其比较表
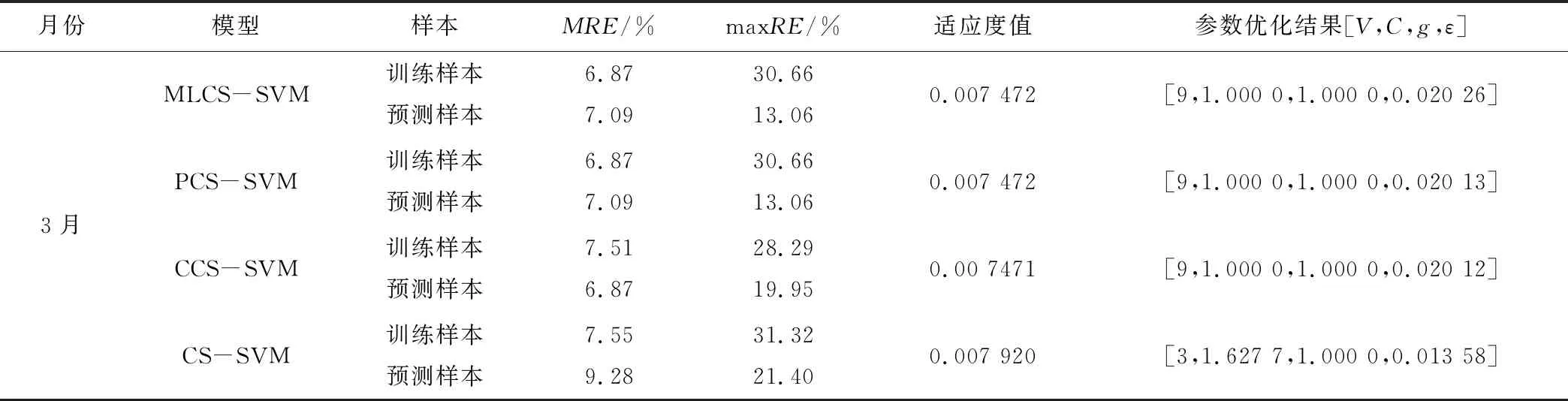
续表3 实例1-3月月径流训练-预测结果及其比较表
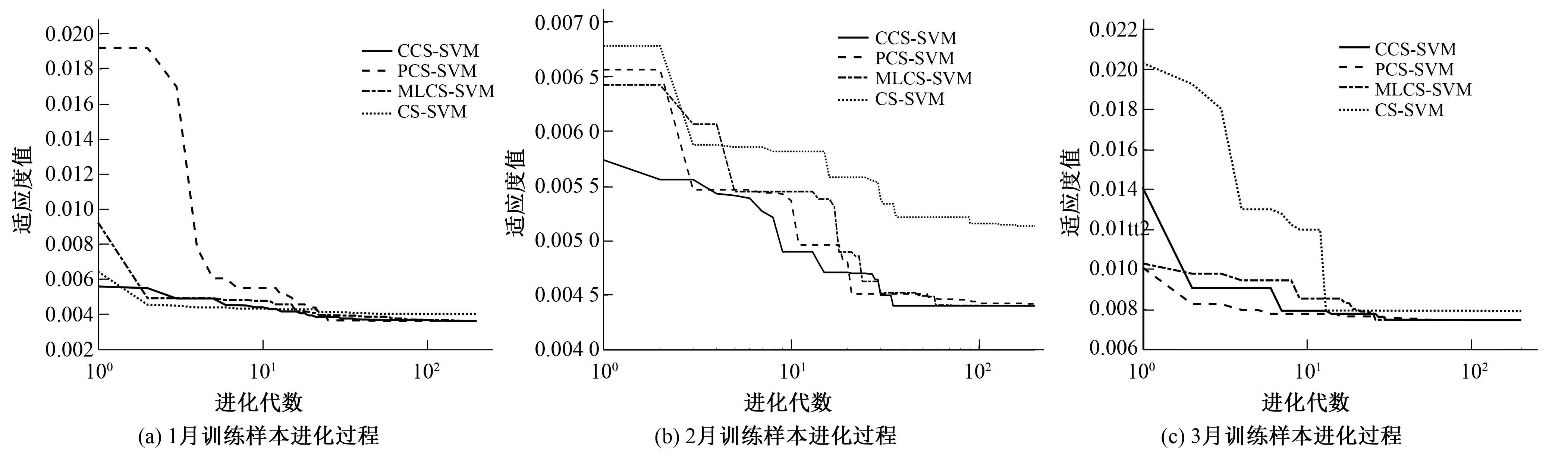
图1 4种模型1-3月训练样本进化过程图

图2 实例1-3月月径流训练-预测相对误差效果图
依据表3及图1~图2可以得出以下结论:
(1)MLCS-SVM、PCS-SVM、CCS-SVM 3种模型对实例1-3月月径流预测的平均相对误差分别在4.89%~4.94%、6.87%~7.07%、6.87%~7.09%之间,预测精度分别较CS-SVM模型提高了34.5%、8.30%、23.6%以上,具有较好预测精度和泛化能力,表明MLCS,PCS和CCS算法均能有效优化SVM交叉验证参数、惩罚因子、核函数参数和不敏感系数,模型及方法可为水文预测预报及其他相关预测研究提供参考。
(2)对SVM而言,交叉验证参数的多少直接影响到SVM预测精度和泛化能力。从本实例优化结果来看,对于1月月径流预测,SVM训练的最佳交叉验证参数为5;对于2月和3月,最佳交叉验证参数为9。可见,通过智能算法寻优交叉验证参数,可避免人为调试的繁琐。
(3)从表3及图1来看,MLCS,PCS、CCS算法优化实例1-3月SVM训练样本获得的适应度值分别在0.003 618~0.003 632、0.004 403~0.004 421、0.007 471~0.007 472之间,均优于标准CS算法,通过实例再次验证了基于Mittag-Leffler、Pareto、Cauchy重尾分布改进的MLCS,PCS、CCS算法能有效增强标准CS算法的种群多样性,进一步提升标准CS算法的全局寻优能力。
(4)从图2来看,4种模型拟合、预测精度由优至劣依次是:CCS-SVM、MLCS-SVM、PCS-SVM、CS-SVM模型。
4 结 论
(1)针对标准CS算法存在早熟收敛和易陷入局部极值的不足,分别提出基于Mittag-Leffler、Pareto、Cauchy重尾分布改进的MLCS,PCS、CCS算法,选取6个标准测试函数对MLCS,PCS、CCS算法进行仿真测试,并与标准CS算法的仿真结果进行比较。结果表明:MLCS,PCS、CCS算法寻优效果均优于标准CS算法,具有较好的寻优精度和全局搜索能力。
(2)首次提出SVM 4参数优化方法,即利用MLCS,PCS、CCS算法同时优化SVM交叉验证参数、惩罚因子、核函数参数和不敏感系数,并给出优化步骤和应用实例,有效拓展了SVM模型的应用范畴。从实例应用效果来看,同时优化SVM 4参数是可行和有效的。
(3)MLCS-SVM、PCS-SVM、CCS-SVM 3种模型对实例1-3月月径流预测的平均相对误差分别较CS-SVM模型提高了34.5%、8.30%和23.6%以上,具有较好预测精度和泛化能力。验证了MLCS,PCS、CCS算法均能有效优化SVM交叉验证参数、惩罚因子、核函数参数和不敏感系数,模型及方法可为水文预测预报及其他相关预测研究提供参考。
□

