例谈数学思想与方法在高中数学问题中的具体体现

◇ 浙江 吴贤盛

数学思想与方法是指引我们分析问题与解决问题的法宝，是数学的灵魂，我们常常在学习和掌握数学知识的同时获得数学思想与方法.作为学习数学不可或缺的一部分，数学思想与方法能够促进学生知识体系的形成.高中数学思想与方法主要包括函数与方程思想、数形结合思想、分类讨论思想、化归与转化思想等，本文结合具体问题谈一下这些思想方法的具体体现.

1 函数与方程思想

例1在等差数列{an}中，已知a1＝13，3a2＝11a6，则数列{an}的前n 项和Sn的最大值为.

由3a2＝11a6，得3×(13＋d)＝11×(13＋5d)，解 得d ＝－2，所 以an＝13 ＋(n－1)×(－2)＝ － 2n ＋ 15. 故 Sn＝所以当n＝7时，数列{an}的前n 项和Sn最大，最大值为S7＝49.

数列的通项与前n 项和可以看成自变量为正整数的函数，用函数的性质去处理数列问题十分重要，本题就是通过写出Sn的关系式，利用二次函数的性质去求解最值的，充分体现了函数与方程思想在高中数学的应用之广泛.除此之外，解析几何、立体几何中也存在着大量的函数与方程思想.

2 数形结合思想

例2已知则f(3－x2)＞f(2x)的解集为( ).

A.(－∞，－3)∪(1，＋∞) B.(－3，1)

C.(－∞，－1)∪(3，＋∞) D.(－1，3)

因此可得f(x)单调递增，f(x)图象如图1 所示，f(3－x2)＞f(2x)可转化为3－x2＞2x，解得－3＜x＜1，故选B.

数形结合思想可以起到以形助数、以数定形的作用.利用数形结合思想可以构建函数模型并结合其图象求参数的取值范围、方程根的范围、量与量之间的关系等，还可以利用几何意义研究函数的最值问题和证明不等式等.本题根据导函数对函数的单调性进行判断，再画出函数图象，易知函数f(x)单调递增，再根据函数的单调性与图象即可求得不等式的解.

图1

3 分类讨论思想

例3已知函数f(x)＝x2－(a＋1)x－4(a＋5)，g(x)＝ax2－x＋5，其中a∈R.

(1)若函数f(x)，g(x)存在相同的零点，求a的值；

(2)若存在两个正整数m，n，当x0∈(m，n)时，有f(x0)＜0与g(x0)＜0同时成立，求n 的最大值及n 取最大值时a 的取值范围.

(1)f(x)＝x2－(a＋1)x－4(a＋5)＝(x＋4)[x－(a＋5)]，所以x1＝－4，x2＝a＋5.由g(－4)＝16a＋9＝0，得由g(a＋5)＝a[(a＋5)2－1]＝0得a＝0，－4或－6.

(2)令f(x)＜0，则－4＜x＜a＋5，因为m，n 为正整数，所以a＋5＞0，即a＞－5，记N ＝(0，a＋5)，令g(x)＜0，即ax2－x＋5＜0的解集为M，则由题意得区间(m，n)⊂M ∩N.

当a＜0 时，因为g(0)＝5＞0，故g(a＋5)＝a[(a＋5)2－1]＜0，即a＞－4或a＜－6，又因为a＞－5，故－4＜a＜0，此时n≤a＋5＜5.又m，n∈Z，所以m＜n≤4.

当a＝0时，M ∩N＝∅，不合题意.

当a＞0 时，因为g(0)＝5＞0，g(a ＋5)＝a[(a＋5)2－1]＞0，故无解.

综上，n 的最大整数为4，此时a 的取值范围为

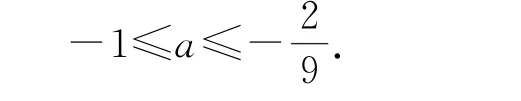
分类讨论思想是高中数学应用最为广泛的数学思想，它能够将数学难题进行分解，逐个击破.应用分类讨论思想时，最为关键的问题在于要能够判断分类讨论的标准，这样方能做到思路清晰.在本题的求解中，a 作为一个参数，首先要根据a是否为0，判断g(x)是否为二次函数，若是二次函数，还需判断开口方向，这就导致在求解第(2)问时要进行分类讨论.

4 转化与化归思想

例4若函数f(x)＝e2x－ax2＋1在[1，2]上是减函数，则实数a 的取值范围是( ).

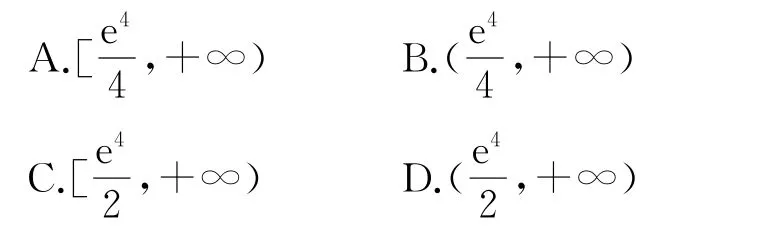
因为f(x)＝e2x－ax2＋1，所以f′(x)＝2e2x－2ax，因为f(x)在[1，2]上是减函数，则e2x－ax≤0在[1，2]上恒成立，即在[1，2]上恒成立，令所以h′(x)＝所以h(x)在[1，2]上单调递增，即所以实数a 的取值范围是故选C.

转化与化归思想是指将问题进行较好地转化，在解题时，利用转化与化归思想可以运用“换元”把式子转化为有理式或使整式降幂等，可以把较复杂的函数、方程、不等式等问题转化为易于解决的问题，也可以把原问题转化为一个易于解决的等价问题，达到化归的目的.在本题的求解中，通过灵活转化使问题获解，其实质就是求解的最大值.