复数型扩展卡尔曼滤波算法在感应电机直接转矩控制系统中的应用

潘京辉 ,张维存

(1.北京科技大学自动化学院,北京 100083;2.工业过程知识自动化教育部重点实验室,北京 100083)

1 引言

磁链观测一直是感应电动机控制中的重要部分,要想获得较高的调速性能,就必须要对电机磁链进行精确的观测[1].为了获得更加准确的电机状态估计以提高调速系统的控制性能,各国学者相继提出了许多状态估计方法,其中比较有代表性的有直接计算法、模型参考自适应推算法(model reference adaptive system,MRAS)、自适应观测器法以及扩展卡尔曼滤波器法(extended Kalman filter,EKF)等[2–6].这3 种方法属于模型确定观测方法,电机参数变化对其观测准确性影响比较大.扩展卡尔曼滤波器属于随机过程估计方法,可以有效的削弱系统噪声和测量噪声的对状态变量估计的影响,对电机参数变化的干扰具有很好的鲁棒性[7–8].采用扩展卡尔曼滤波器对感应电机进行状态估计,能同时给出电机磁链和转速的估计值.

由于交流电动机是一个多变量、强耦合的非线性系统,对其进行动态系统建模得到的系统状态矩阵也是一个高阶矩阵[9–11].系统的复杂性增加了观测器设计的难度,而且在观测器进行状态估计时运算量也会非常大,这样降低了观测器的响应速度,同时也使得调速系统控制性能大打折扣[12–13].为此,许多学者提出了使用降维观测器来对系统状态变量进行估计.Francesco Alonge等于1990年提出了变结构降维磁链观测器[14];翁海清等于2001年提出了基于H∞控制理论的降维观测器[15];武明珠等于2012年提出了基于降维EKF的转速磁链观测器[16];在2007年Francesco Alonge等提出了降维磁链优化观测器[17],其后又于2014年提出了基于复数模型的扩展卡尔曼滤波器对模型进行降维,在感应电机转子磁链估计中使用复数型扩展卡尔曼滤波器,并将其状态估计值应用于电机矢量控制系统,取得了比较理想的效果.

复数型扩展卡尔曼滤波器是近年来国外学者提出的比较新颖的概念,通过对控制系统建立复数数学模型,使系统状态矩阵维数得到降低,在理论计算和硬件实现上会带来很大的便捷,有效减少了数字信号处理器(digital signal processor,DSP)的运算时间;而且比起全阶状态观测器,复数型扩展卡尔曼滤波器也能获得准确的状态估计,同时也具有很强的鲁棒性.

本文首次将复数型扩展卡尔曼滤波器应用于感应电机转速和定子磁链进行估计,采用复数模型进行滤波器设计有效减少DSP运算量,降低延迟,提高响应速度,在电机启动和加速时也能具有较高的观测精度.这些特点改善了感应电机无速度传感器控制系统的调速性能.本文首先建立了感应电机的复数数学模型,然后对模型进行离散化并分析了离散化后感应电机的复数数学模型的可观性,证明了该模型的局部可观性.基于此,推导得出了感应复数型扩展卡尔曼滤波器的表达式,并将该滤波算法应用于感应电机直接转矩控制中;最后通过仿真和实验证明了该方法的有效性和可行性.

2 感应电机的复数数学模型[18]

在两相静止坐标系下,三相感应电机的状态方程式可表示为

式中:

isα和isβ是定子电流,usα和usβ为定子电压,ψsα和ψsβ是定子磁链. Rs和Rr分别是定子电阻和转子电阻,ωr是转子电磁转速,Lsd和Lrd分别是定子和转子电感,Lmd为互感,np为电机极对数,JM为电机转动惯量,TL为负载转矩.

当转速在两个相邻采样时刻间变化很小时,方程组(1)中的最后一式将等于零,即转速变化率为零,这种处理方式在卡尔曼滤波器设计的建模过程中被广泛采用[8,13,19],它所造成的转速估计误差可简单归结到系统噪声中,电机模型的精度不会受到影响.为建立感应电机复数数学模型,定义状态变量复数形式如下:

式中j为虚数单位.

选取定子电流作为输出,定子电压作为输入,状态方程式(1)变为如下形式:

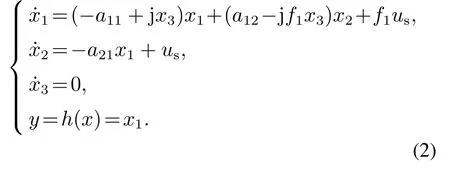
上式就是三相感应电动机复数模型的状态方程式.从维数上看,采用复数模型后状态方程式由5维减少了3维,这对之后的模型可观性分析和滤波器设计带来了很多方便.

3 感应电机的复数数学模型离散化及可观性分析

3.1 感应电机的复数数学模型离散化

为了设计卡尔曼滤波器并在DSP上实现滤波器功能,需要先对式(2)中的感应电机复数模型进行离散化.取采样周期为Ts,经过离散化后其状态方程式为

3.2 感应电机的离散复数模型可观性分析

下面将对第3.1节中得到的离散复数模型进行可观性分析.首先令x(k+1)gk(x(k),us(k)),即

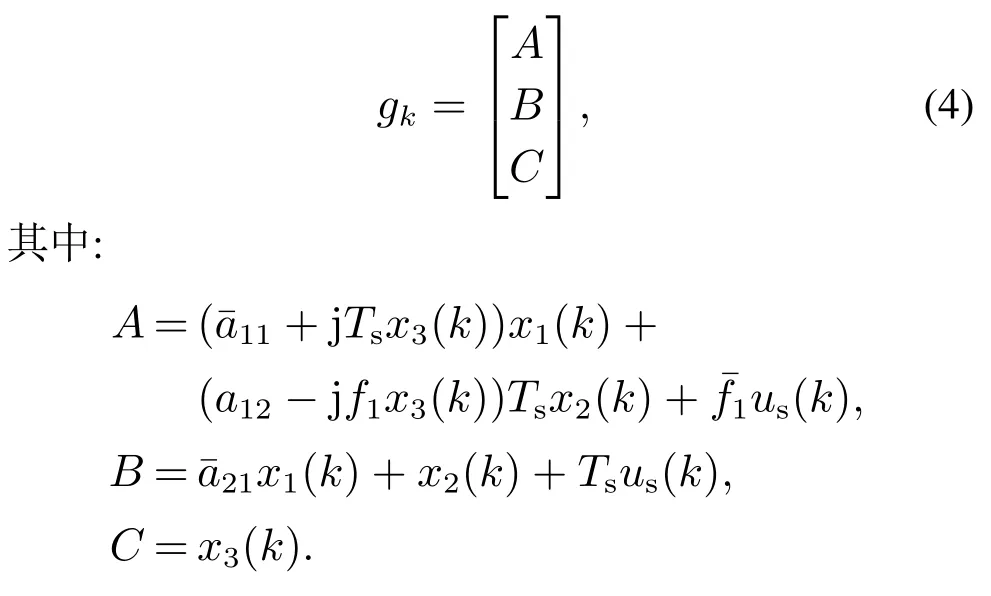
gk在x(k)处的雅克比矩阵为

则可观性矩阵O可表示为[20]

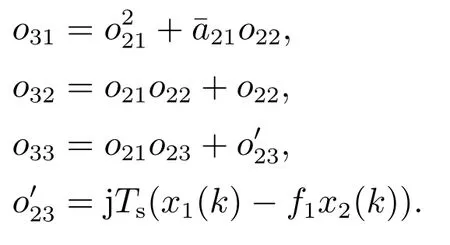
经过直接计算,可观性矩阵O的行列式值为

式中:由于Ts>0,a12−jf1x3(k)0,因此式(3)中的感应电机离散复数模型局部可观性条件为

注意到式(3)中第2项:

整理得

显然,x2(k)的差分与x1(k)差分没有比例关系,因此式(4)中感应电机离散复数模型局部可观性条件成立,即式(3)中感应电机离散复数模型局部可观.

4 复数型扩展卡尔曼滤波器设计

前文已证明了感应电机离散复数模型的局部可观性,这里本文将在感应电机复数模型的基础上,推导出感应电机复数型扩展卡尔曼滤波器的表达式,以实现对感应电机转速和定子磁链的估计.

4.1 感应电机离散随机模型

为推导出复数型扩展卡尔曼滤波观测器(extended complex Kalman filter,ECKF)表达式,这里先给出感应电机离散随机模型:

其中: gk表达式如式(4)所示,ωk,νk分别为系统噪声和输出测量噪声,二者都是均值为零的高斯白噪声,且互不相关;分别用Q,R表示其协方差矩阵.

与普通扩展卡尔曼滤波器设计方法相同,复数型扩展卡尔曼滤波器设计分为两个步骤:第1个步骤称为预报阶段,该步骤主要是计算状态预报值和状态误差协方差矩阵预报值这两个量,得出状态先验估计;第2个步骤称为更新阶段,在该步骤中将要计算出所构造的扩展卡尔曼滤波器的增益,进行状态误差协方差矩阵的更新,还要对所预报的状态值进行更新,得出状态后验估计.其结构图如图1所示.

4.2 复数型扩展卡尔曼滤波器的表达式

本文设计的ECKF与EKF有相同的结构,但ECKF的状态估计误差协方差矩阵为厄米特矩阵即

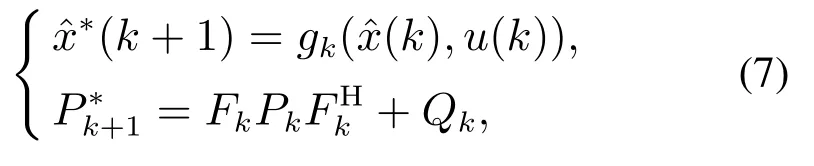
式中:

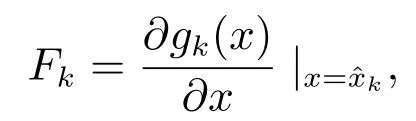
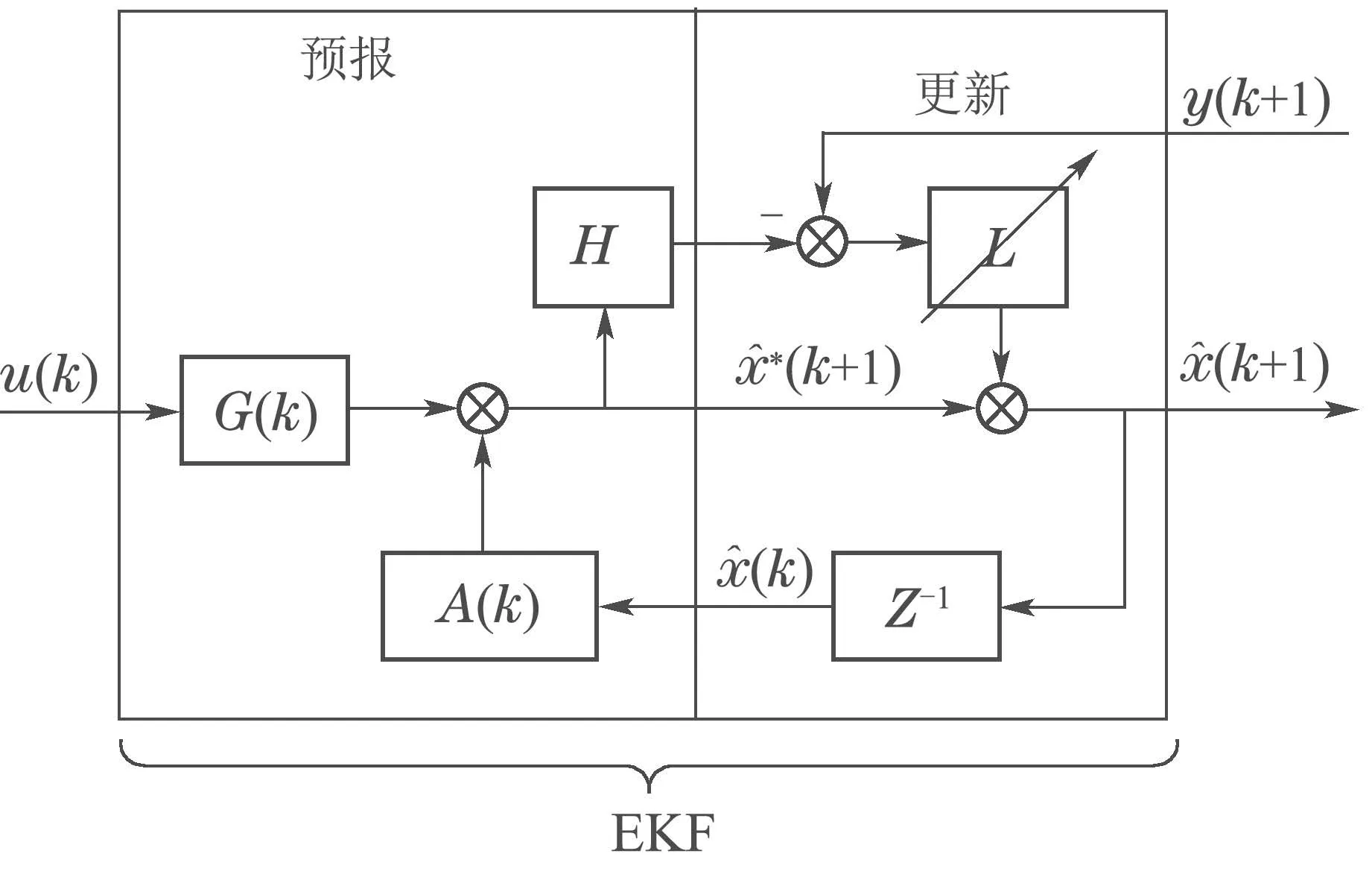
图1 扩展卡尔曼滤波器结构图Fig.1 The structure of extended Kalman filter

由上述推导过程可以看出,复数型扩展卡尔曼滤波器的表达式是一个由式(7)–(8)组成的递归表达式.

4.3 复数模型减少计算量的分析

本文采用复数模型进行滤波器设计,有效地减少了滤波算法的计算量,复数模型之所以能降低运算量,减少运算次数其主要原因总结为如下3点:

1)滤波器维数降低减少了运算次数,采用复数模型,与EKF相比,ECKF维数从5维降低到了3维,在状态方程求解运算的过程中有效地减少了运算次数;

2)不包含矩阵求逆运算,在整个滤波算法实现过程中,没有用到矩阵求逆的运算,相比EKF在求解Lk的过程中需要进行一个二阶矩阵求逆的运算,ECKF算法中Lk为一个实数;

3)输出矩阵Hk中零元素减少,在EKF中输出矩阵Hk是一个2×5的矩阵,其中有8个零元素,这在运算过程中带来了很多不必要的计算,占用DSP资源,而在本文设计的ECKF中Hk为一个1×3的矩阵,有2个零元素,有效减少了运算量;

基于上述因素,采用复数型扩展卡尔曼滤波器使感应电机数学模型得到了降维,减少了计算机运算次数,避免了不必要的计算,使DSP的运算时间得到了降低,提高了滤波器状态估计的快速性.

5 仿真与实验研究

设计采用MATLAB/Simulink对提出的感应电机复数型扩展卡尔曼滤波器进行仿真,以验证其有效性和准确性.感应电机主要参数:额定电压UN380 V,额定频率fN50 Hz,额定转速nN1440 r/min,定子电阻Rs1.405 Ω,转子电阻Rr1.395 Ω,定子自感Lsd0.1780 H,转子自感Lrd0.1780 H,互感Lmd0.1722 H,极对数np2,转动惯量J0.511 kg·m2.

在仿真模型中,复数型卡尔曼滤波器先对感应电机定子磁链和转速进行状态估计,再将得到的估计值反馈到直接转矩控制系统,形成转速和磁链双闭环控制,其系统结构如图2所示.

图2 感应电机直接转矩控制系统结构图Fig.2 The structure of induction motor direct torque control system

进行仿真时,先给定电机转速为600 r/min,定子磁链幅值给定为1 Wb,到1 s转速平稳后再重新给定转速为800 r/min,定子磁链幅值不变.仿真时间2 s,仿真结果如图3–5所示.

图3 转速估计仿真结果Fig.3 Simulation results of rotor speed estimation

图4 α轴定子磁链估计仿真结果Fig.4 Simulation results of stator flux estimation in α axis

从图3可以看出,ECKF估计转速能很好地跟随实际转速变化,即使在电机启动和加速时也能保持良好的收敛性和准确性;当电机达到设定转速稳定运行时,转速估计误差就会迅速收敛到零.图4显示,ECKF对电机定子磁链的估计误差始终保持在0.04 Wb以下,满足磁链精度要求.图5表明定子磁链从仿真开始后迅速增大到设定值(1 Wb),同时按逆时针方向旋转,最终形成了磁链圆环.

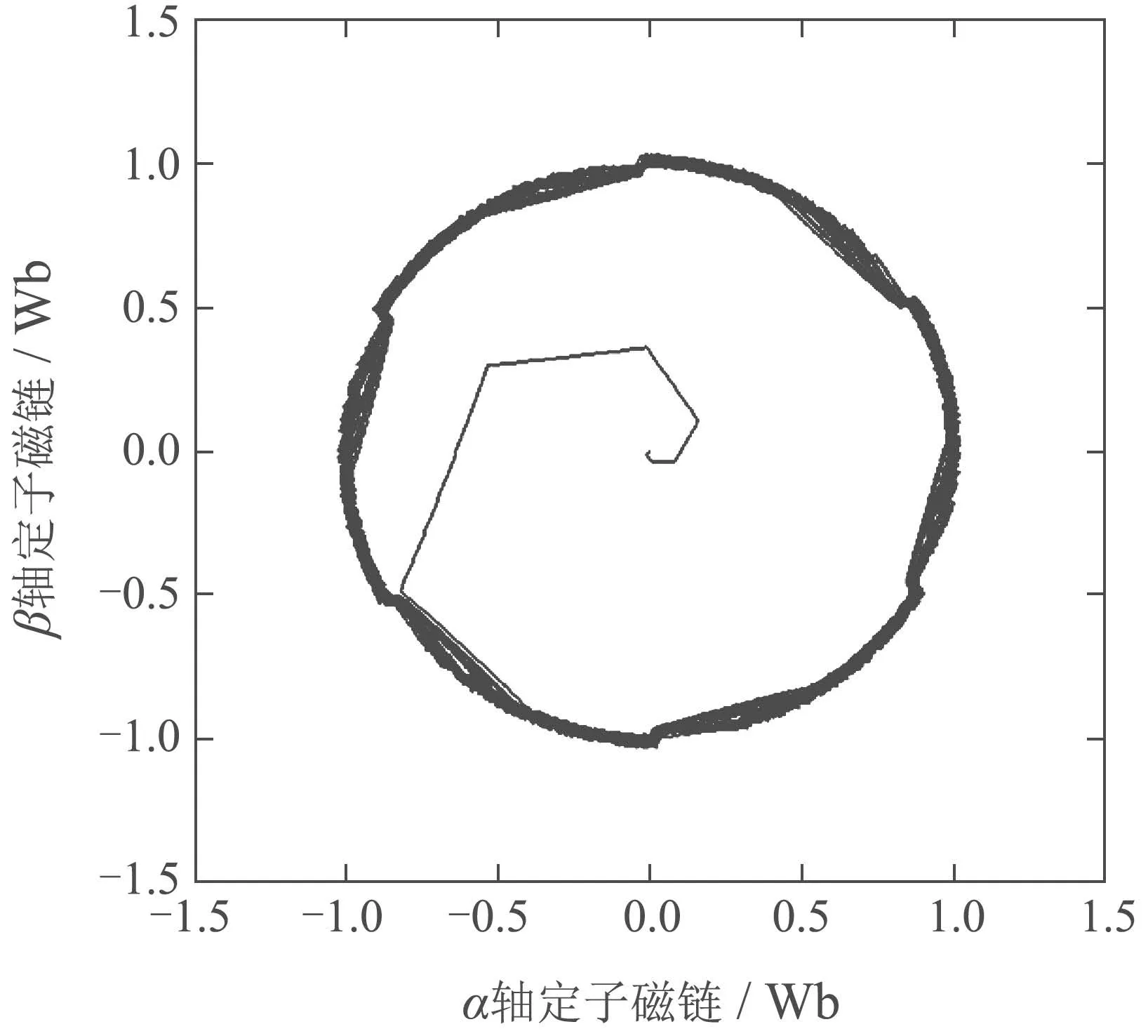
图5 ECKF定子磁链估计(α–β轴)Fig.5 Simulation results of stator flux estimation(α–β axis)

为在MATLAB仿真中计算复数型扩展卡尔曼滤波器算法和扩展卡尔曼滤波器算法的执行时间,在仿真用tic和toc监控程序的运行时间,得出扩展卡尔曼滤波器算法的单次执行时间为6µs,复数型扩展卡尔曼滤波器算法的单次执行时间为2µs,仿真结果验证了ECKF算法能够有效减少计算量.

同时为了验证的感应电机复数型扩展卡尔曼滤波器的实际可行性,搭建了实验平台进行实物实验,主要包括感应电机及负载、主回路、PC、DSP(TMS3–20F2812)控制板,如图6所示.

电机参数同仿真参数.实物实验时使电机在与仿真同样的条件下运行和加速,实验中用同样的方法整定得到噪声协方差矩阵R1,Qdiag{1,10−4,20}.复数型扩展卡尔曼滤波器通过DSP来实现,其转速和定子磁链估计结果直接反馈到转速控制的直接转矩控制(direct torque control,DTC)模块,实验结果如图7–8所示.

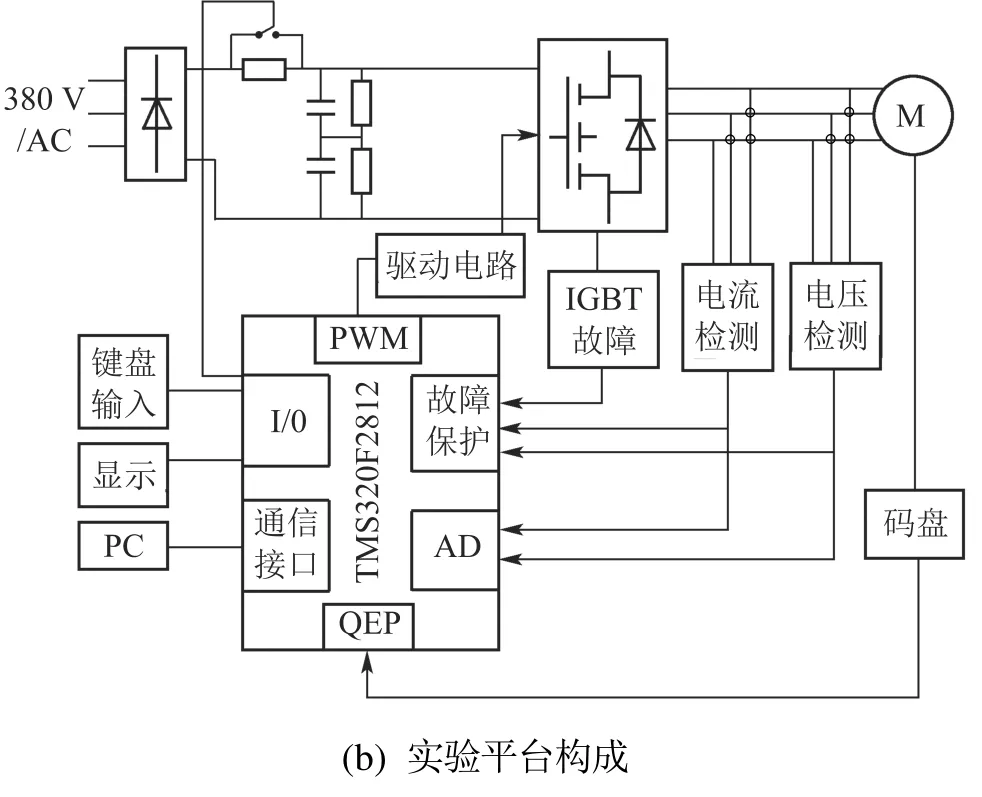
图6 实验平台及其构成Fig.6 The experiment platform and its components

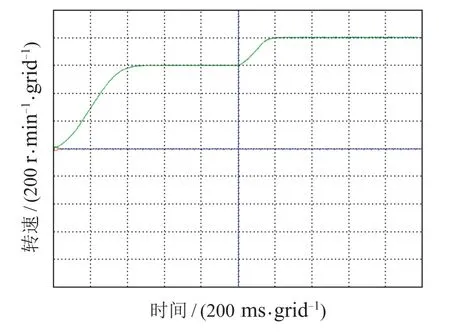
图7 感应电机转速响应(实验结果)Fig.7 The induction motor rotor speed response (experiment result)

图8 感应电机定子磁链(实验结果)Fig.8 The induction motor stator flux response(experiment result)

对比图3(a)和图7可以看出,仿真结果和实验结果得到的转速变化曲线趋势一致,电机转速能迅速增加到设定转速,并根据设定值变化进行转速调整.实验结果图7显示,感应电机转速自调整到仅用了不到0.2 s的时间,验证了DTC控制算法的有效性,同时也表明了ECKF对转速和定子磁链估计的快速性和准确性,足以满足DTC控制的实时需求.图8显示,在实验过程中定子磁链始终收敛于单位圆上,符合定子磁链幅值的预先设定1 Wb.实验结果证明了复数型扩展卡尔曼滤波器的实际可行性.同时为计算实验中复数型扩展卡尔曼滤波器算法子程序在DSP中的执行时间,在子程序运行开始,置一个引脚为高电平,退出子程序时为低电平,并利用示波器进行观察得到实验中复数型扩展卡尔曼滤波器算法执行时间约为1.2µs,同理得到实验中扩展卡尔曼滤波器算法执行时间约为3µs,实验结果说明了ECKF算法能够明显减少DSP的计算量,验证了该方法的有效性.

6 结论

本文提出了一种感应电机复数型扩展卡尔曼滤波器,首次将复数型扩展卡尔曼滤波器应用于感应电机转速和定子磁链进行估计.经理论推导及仿真和实验验证得出以下结论:

1)复数形式的感应电机离散数学模型具有局部可观性,满足滤波器设计条件;

2)采用复数模型进行滤波器设计可以有效减少DSP运算量,降低延迟,提高响应速度,在电机启动和加速时也能具有较高的观测精度.这些特点改善了感应电机无速度传感器控制系统的调速性能;

3)仿真和实验结果表明,本文提出的感应电机复数型扩展卡尔曼滤波器对转速和定子磁链估计具有较高准确性和快速性,足以满足DTC控制的实时需求.实物实验验证了感应电机复数型扩展卡尔曼滤波器的有效性和可行性.