初中数学中的数列规律问题的探究
江苏省泰州二附中(225300) 邓小卿
初中数学中常常需要解决探求一列数的排列规律问题,这不能不说是一大难点.因此如何指导学生迅速地发现规律,并能正确地表达规律就显得尤为重要,如果方法得当,不仅能开发学生的智力,而且能够提高学生的学习兴趣.鉴于有所侧重,某些问题,本文只讲方法,暂不作理论上的推导,下面介绍几种常用的解决方法.
我们首先约定:数列中的第1 项用a1表示,第2 项用a2表示,······,第n项用an表示.这里1,2,···,n谓下标,所谓规律就体现在每一项都能与“标”挂上钩.
方法1略施变更现原形
把所给数列中的每一项都加或减、或乘或除以同一个数,也许就能得到一个我们所熟悉的数列.
例1 求数列:0,7,26,63,124···的第n项
解:把这个数列的各项都加上1,得:1,8,27,64,125···
即13,23,33,43,153,···
因此原数列的第n项为n3-1.
例2如图,每个正方形点阵被一直线分成两个三角形点阵,根据图中所提供的信息,用含n的等式表示第n个点阵中的规律.(泰州中考数学,2006年)

解:第1 个等式,即0+1=12,
把被加数、加数、和分别列出,得到三个数列:
被加数列:0,1,3,6,···
加数列:1,3,6,10,···
和数列:12,22,32,42,···
易知和数列的第n项为n2,加数列中的第n项为被加数列中的第n+1 项,只要能求出被加数列的第n项就能很快得到加数列的第n项.把被加数列的各项都乘以2,得0,2,6,12,···,即:0×2,1×2,2×3,3×4,···,则第n项为(n-1)n,因此被加数列的第n项为那么加数列的第n项就是因此,第几个点阵中的规律就是:
方法2拆分各数求规律
把所给数列中的每一项拆成与项数有关的几个数的和或差或积或商或方的形式,从中找出变化规律.
例3把数列:2,1/2,4/3,3/4,6/5,5/6,···,的第n项用n的代数式表示出来.
解:分母的规律显而易见,只要求出分子所构成的数列的第n项即可这里a1=2=1+1,a2=1=2-1,a3=4=3+1,a4=3=4-1,···,再考察数列1,-1,1,-1,···,的变化规律,奇数项为+1,偶数项为-1.进而写成a1=1+(-1)1+1,a2=2+(-1)2+1,a3=3+(-1)3+1,a4=4+(-1)4+1.因此,该数列的第n项就是[n+(-1)n+1]/n
例4正整数按如图所示的规律排列,请写出第20 行第22 列的数字.

解:让我们先看看第1 行第3 列,2 行4 列,3 行5 列,4行6 列有哪些数字.得5,11,19,29,···,找出变化规律,把第n行第n+2 列的数表示出来,先把这组数都加上1,得6,12,20,30,···,拆法如下:6=2×3,12=3×4,20=4×5,30=5×6,···,那么这列数的第n个是(n+1)(n+2)-1,从而5,11,19,29,···,这列数的第n个是(n+1)(n+2),这就是数表中第n行第n+2 列的数.因此第20 行第22 列的数字为(20+1)(20+2)-1=461.
方法3由后向前搞递推
对所给数列从第2 项起,找出后项与前项的关系(往往是求差)得到若干个等式,再把这些等式迭加起来,就能得到通项的表达式.这种方法对解决图形的生长问题颇具成效.
例5如图是用相同的长度的小棒摆成的一组有规律的图案,图案(1)需要4 根小棒,图案(2)需要10 根小棒,······,按此规律摆下去,第n个图案需要小棒____根(用含n的代数式表示).(陕西太原中考数学,2011年)

解:这里a1=4,a2-a1=6,a3-a2=6,a4-a3=6,···,an-an-1=6,把这几个等式左右两边分别相加得:
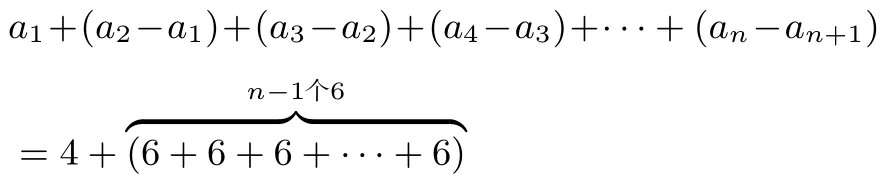
即:an=4+6(n-1)=6n-2.
例6将一些相同的“○”,按如图所示的规律依次摆放,观察每个“电图”中的“○”的个数,若第n个“电图”中有245个“○”则n=____.(四川绵阳中考数学,2012年)

解:这里a1=5a2-a1=2=1×2,a3-a2=4=2×2,a4-a3=6=3×2,···,an-an+1=(n-1)·2,把这n个等式的两边分别相加得:

即an=5+n·(n-1),当an=245时得方程5+n·(n-1)=245,解得n=15
例2.例4 亦可用此方法,读者不妨试试.
方法4按阶设立函数式.
一般地说:数列的通项an是n的函数,其中自变量n为正整数.
例7求5,30,8,23,11,16,14,9,···,的第99 项和第100项.
解:把数列的奇数项单独列出得:5,8,11,14···这是第1,3,5,7,···,项,后项与前项之差为3,这是原数列中,中间去掉一项的差,如按规律补上则得到的数列:5,6,5,8,9.5,11,12.5,14,···,其公差就是1.5,这个数列的第n项an就是n的一次函数,且n的系数就是1.5,
设an=1.5n+c,由a1=5.得5=1.5×1+c,c=3.5.
于是有an=1.5n+3.5(n为奇数),这就是原数列中奇数项的表达式,
再把原数列的偶数项单独列出得:30,23,16,9,···,其公差为+7,按规律补上第1,3,5,7,···,项得到:33.5,30,26.5,23,19.5,16,···,其公差为-3.5.
设an=-3.5n+e,由a1=33.5 得33.5=-3.5+e,e=37.
于是得an=-3.5n+37(n为偶数).这就是原数列中偶数项的表达式,所以
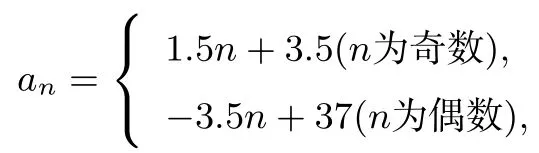
当n=99,a99=1.5×99+3.5=152
当n=100,a100=-3.5×100+37=-313.
例8与例6 时数据间,求数列5,7,11,17,···,的第n项
解:把后项与前项的差记下,并反复运用这一做法:
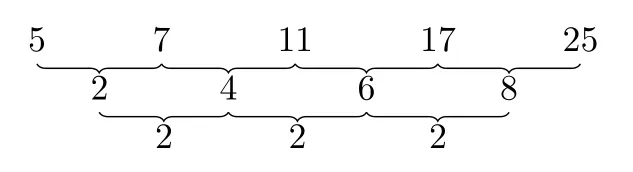
经过两次求差,始得常数,那么通项an是n的二次函数,此数列是二阶等差数列,设an=bn2+cn+d
把n=1,an=5;n=2,an=7;把n=3,an=11 代入
所以an=n2-n+5.
例9 求数列:1,3,17,55,129,25,1···,的第n项
解:反复求差:
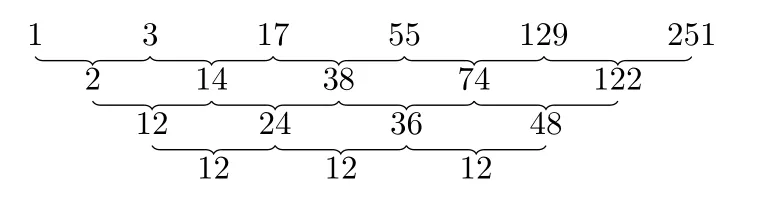
历经三次求差,始得常数,那么通项an是n的三次函数,此数列称为三阶等差数列,设an=bn3+cn2+dn+e
把n=1,an=1;n=2,an=3;n=3,an=17;n=4,an=55 代入

所以an=2n3-6n2+6n-1.
顺便指出,无论用哪种方法求出通项的表达式以后,都要进行检验,如果an与标n对不上,则已经出错,查出问题出在哪里或换一种方法重新来过.
解决数表,数阵等复杂问题,只要找出与提出问题有关的某一数列,即某一横行或某一纵列或某一斜行或前排或后列或某“框”内的数时排列规律,就能把研究庞杂的表、阵转化为讨论单一的数列,取得了事半而功倍的成效,有时甚至一步到位.例4 就是采用了这一做法.

