用对数均值不等式证明数列不等式
2020-08-06 11:56屈惠鹏韩改琴
高中数学教与学 2020年13期
屈惠鹏 韩改琴
(陕西省商洛中学,726000)
在数列不等式中,有一类含有lnn的不等式,它的一般证法是利用导数先证明一个关于lnx的函数不等式,再用赋值法证明关于lnn的不等式.这种证法技巧性强,步骤较多,过程冗长,学生不易掌握.若利用对数均值不等式来证明这类不等式,可以避免从实数向自然数的过渡,直接从自然数开始证明,化繁为简、化难为易,收到事半功倍的效果.

(*)
该不等式的证明参见文[1].本文举例说明这个不等式在证明数列不等式时的应用.

(1)求a的值及f(x)的最大值;
解(1)略.
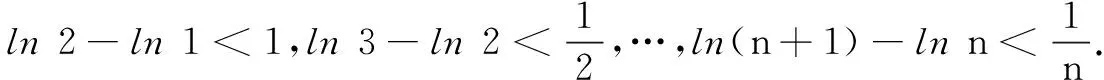
变式1已知函数f(x)=(x+1)lnx-ax+2.
(1)若f(x)定义域上具有单调性,求实数a范围;
解(1)略.
变式2(2012年天津高考题)已知函数f(x)=x-ln(x+a)的最小值为0,其中a>0.
(1)求a的值;
(2)若对任意的x∈(0,+∞),有f(x)≤kx2,求实数k的最小值;
解(1)(2) 略.

评注本题需将对数均值不等式与放缩法综合使用,达到证明的目的.


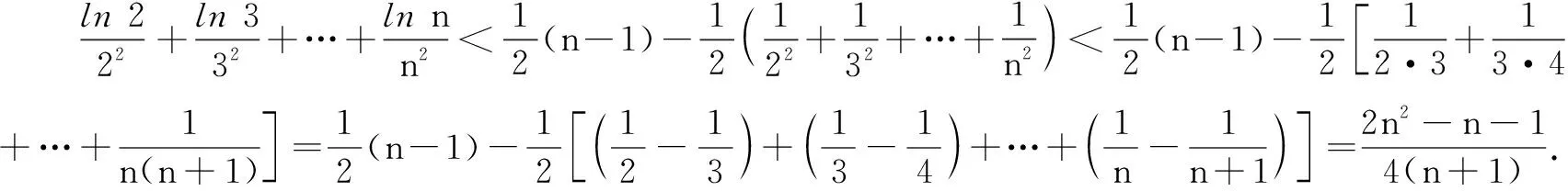
例3已知函数f(x)=tx-t-lnx.
(1)若函数f(x)在[1,+∞)上增函数,求实数t的范围;
(2)当n≥2且n∈N*,证明:
解(1)略.

评注本题需在不同区间[k,k-1]及[k,1]反复使用对数均值不等式,以达到证明的目的.

(1)用a表示出b,c;
(2)若f(x)≥lnx在[1,+∞)上恒成立,求a取值范围;
解(1)(2) 略.
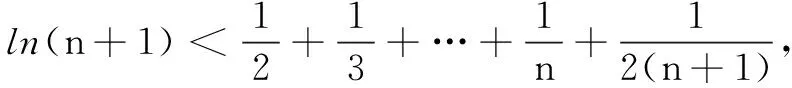

(1)当x≥0时,f(x)≤0,求λ的最小值;
解(1)略.
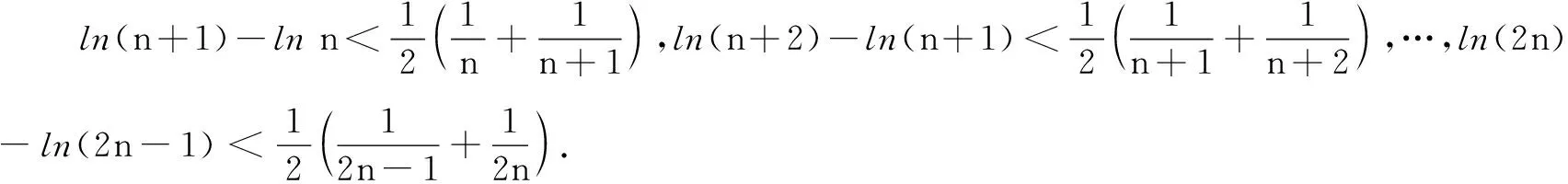
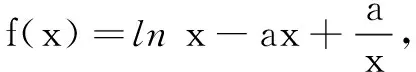
(1)讨论函数f(x)的单调性;
(2)若n∈N*,且n≥2,证明:
解(1) 略.

由以上例题可见,使用对数均值不等式时,需选择合适的区间,必要时还需与其它不等式或不等式放缩法综合使用,方能达到证明的目的.
猜你喜欢
语数外学习·初中版(2022年3期)2022-05-25
数学物理学报(2022年2期)2022-04-26
新世纪智能(数学备考)(2021年9期)2021-11-24
新世纪智能(数学备考)(2020年9期)2021-01-04
天府数学(2020年3期)2020-09-10
语数外学习·初中版(2020年2期)2020-09-10
河北理科教学研究(2020年1期)2020-07-24
中学生数理化·高一版(2018年10期)2018-11-08
中学生数理化·七年级数学人教版(2018年3期)2018-05-30
中学生数理化·中考版(2017年3期)2017-11-09

