非常规分式最值问题解题策略

李秀元

(湖北省武穴市实验高级中学，435400)

近几年,各地高考模拟不断出现非一次分式最值问题.主要以分析和构造能力为着眼点,考查学生数学建模和逻辑推理等核心素养．此类试题解法具有一定的灵活性,学生若不积累一定的解题经验,没有熟悉的思想指导,处理起来还是普遍感觉比较困难．本文对此类问题分类例析,供参考.

一、直接运用基本不等式

应用基本不等式解决最值问题,是高考的基本考点.此类题型的条件与结论的关系有时具有一定的隐蔽性,表面上不能直接套用基本不等式,但稍微变通一下,还是能转化成为基本不等式可求解的类型.

1.一次性使用基本不等式型

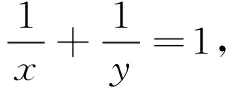
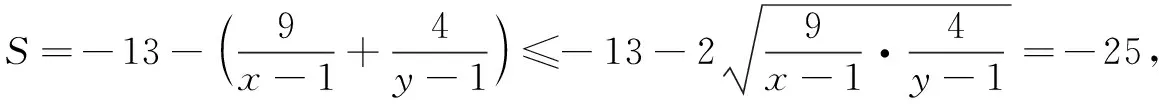
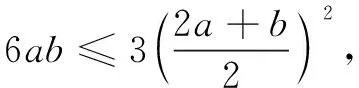
评注寻找基本不等式的结构特征是解这类题的关键,化简与化归是根本,如配凑结构、消元、一次分式结构的分离常数及二次分式结构的降次等．其中,对和积混合型、整式和与分式和混合型的问题，特别要引起重视.

2.多次使用基本不等式型

有些最值问题一次性使用基本不等式并不能解决问题,需要将目标式进行一定形式的转化与重组,多次使用基本不等式方能解决问题.此时，求最值需要特别关注等号成立条件的一致性,否则易产生错误的结果.

(A)4 (B)7.5 (C)8 (D)16

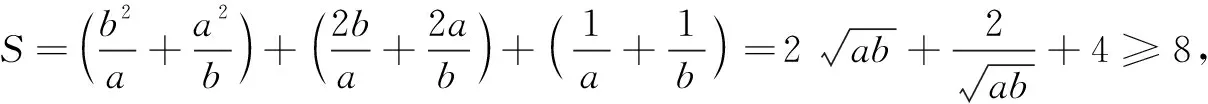
所以m≤16,即m的最大值为16.

二、换元法转化

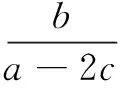
评注换元法是沟通数学不同模型之间相互联系的重要桥梁.本题借助圆的参数方程,将目标函数简化表示,再借助表达式的几何意义使问题获解,彰显了换元法能变换问题表达方式,有利于拓展思路,灵活解题.

三、减元法与函数思想

对多元变量的最值问题,若能通过消元化简回归一元函数,就可以化陌生问题为熟悉问题,顺利实现问题的求解.

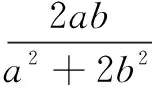
本文仅对此类问题最常见类型的求解作了简单的分类,但并不意味着此类问题就只能按这一固定方式求解,很多问题是可以多角度思考的,解题时应注意灵活选择解决方法,并不断进行归纳、创新．另外,作为小题是有解题时间限制的,由于这类问题的综合性较强,难度较大,平时训练不宜选用过于复杂的题目.