例谈用蒙日圆命制试题的几个视角
魏东升
(江西省瑞金市第一中学,342500)
作为圆锥曲线大家庭中的重要一员,圆及其相关知识一直是高考数学命题考查的重点之一;同时,像阿波罗尼斯圆、蒙日圆等隐形圆也频繁地出现在考题中.然而,不少学生甚至教师对此类隐形圆并不够熟悉,以致在面对这类问题时常常感到棘手.为此,笔者就圆锥曲线中的蒙日圆及其相应结论粗谈自己的一点拙见.
一、圆锥曲线中的蒙日圆
在有心二次曲线中,任意两条相互垂直的切线的交点都在同一个圆上,它的圆心是有心二次曲线的中心,半径由有心二次曲线的二次项系数决定,这个圆就是蒙日圆.相应结果用符号语言可表示为如下两个结论.

该结论再一次体现了有心二次曲线所具有的统一美、形式美及和谐美,而抛物线虽然没有类似的美,却有类似的结论,只不过其对应的轨迹是一个广义上的蒙日圆——直线.
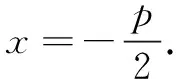
二、 结论的证明
上述结论2的证明较为简单,请读者自行推理.以下给出结论1的证明.
证明设点P(x0,y0),当题设中的两条直线斜率存在且不为0时,设其斜率分别为k1和k2,并设经过点P的切线方程为y=k(x-x0)+y0.与曲线C的方程mx2+ny2=1联立,消去y并整理,可得
①

当m+nk2=0时,① 式为关于x的一次方程,即不存在满足题意的两条相互垂直的切线.
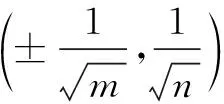

三、试题的命制
结合上述结论,笔者以圆锥曲线和蒙日圆为背景,分别从求参数取值范围、最值问题和求轨迹方程等三个视角对试题命制进行了尝试,以抛砖引玉.
视角1求参数取值范围
例1已知圆C1:x2+y2=1,若直线y=kx+2上总存在点P,使得过点P作圆C1的两条切线相互垂直,则实数k的取值范围是______.

评注设计此题的目的主要是为了考查由直线与圆的位置关系求参数.在此思想指导下,也可以设计蒙日圆与其他圆锥曲线的位置关系问题,进一步还可以求圆锥曲线的离心率、双曲线的渐近线等等.比如


视角2求最值
例2已知点A在抛物线C:y2=4x上,点B(0,1),点P是抛物线C1的两条相互垂直切线的交点,则AB+AP的最小值为______.



视角3求轨迹方程

(A) 圆 (B)椭圆
(C) 圆的一部分 (D)椭圆的一部分
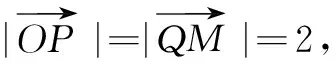
评注本题以蒙日圆为背景,同时考查求轨迹方程时对所求方程的纯粹性和完备性的关注度.
变式设抛物线C:y2=4x的焦点为F,过F且斜率为k(k>0)的直线l与C交于A,B两点,|AB|=8.
(1)求l的方程;
(2)点P是抛物线C1的两条相互垂直切线的交点,求过点A,B且与点P的轨迹相切的圆的方程.
解(1)y=x-1.(过程略)

解析几何相关知识除了能够很好地向学生渗透各种数学思想方法,更是可以培养学生数学运算、数学建模和逻辑推理等数学核心素养.在此基础上形成对知识的应用意识和创新意识,最终落实“立德树人”的根本目标.而正是由于解析几何的“责任重大”,在教学过程中对学生的要求较高,从而令不少学生心生畏惧.因此,在解析几何的教学中,合适的教学模式的选择显得尤为重要.像以小专题的形式介绍高考中存在的各种隐形圆,短、平、快地一次性彻底解决与其有关的问题,不失为一种好的选择.

