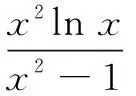中学生核心素养的培养——以数学错题评析为例

许 兵

(江苏省常州市第二中学，213000)

错题再错是教学过程中师生的“永恒话题”.错题再错原因之一是学生在初次犯错或迷路时,老师未能及时按照学生的“意图”来剖析错因或指点迷津,取而代之的是采用“自编→自导→自演”式讲解.有时为了追求教学进度或课堂容量,一个错题、两个变式、三个注意点就结束一道错题的评析,在整个过程中,学生的思维始终被老师牵着鼻子走,更达不到与学生思维碰触出火花的效果.如此的错题评析,忽视从学生的视角剖析错题,错失学生思维能力及数学素养提升的良机,教学效果事倍功半.既未达到“传道授业解惑”的具体教学目的,又与课程总目标的实施相违背,最终未能提升学生作为现代社会公民所应具备的数学素养,同时也没有促进学生自主、全面、可持续地发展.笔者将自己教学过程中遇到的两个错题评析案例整理如下,与读者交流.

案例1已知函数f(x)=x3-x+6lnx,问是否存在实数m,使得函数f(x)的图象上任意不同的两点A(x1,f(x1)),B(x2,f(x2))连线的斜率大于m?若存在,求出m的取值范围;若不存在,请说明理由.

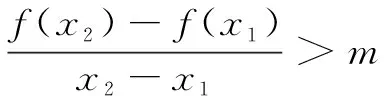
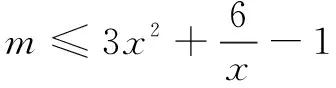
师:两位同学至少有一人结果有误!等号能否取到?(学生沉思中…)过程比结果更重要!生1移项、构造函数、利用函数的单调性求出参数范围,思路很清晰,其他同学对此做法有异议吗?

生3:g(x)在(0,+∞)上单调递增与g′(x)≥0在(0,+∞)上恒成立不等价,虽然结果正确,但缺少检验g(x)在(0,+∞)任意子区间不为常函数的过程.(话音刚落,众生鼓掌)

师:很好!思维很缜密!在利用化归思想将问题从一种形式向另一种形式转化时过程必须等价.那么对生2的做法,其他同学有什么思考吗?(增强学生学习兴趣和自信心,不直接否定学生的想法)

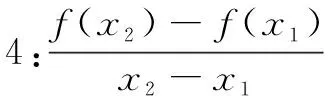
生5:可以作出f(x)=x3-x+6lnx的图象，再结合图象研究它的性质(如图1).

师:很好!形助数,数辅形,利用数形结合的思想研究函数有关问题，可以使我们事半功倍,结合图象请对生2的结果做进一步的分析和探究.(为了图象的直观性,笔者将x轴与y轴的比例做了适当的调整)

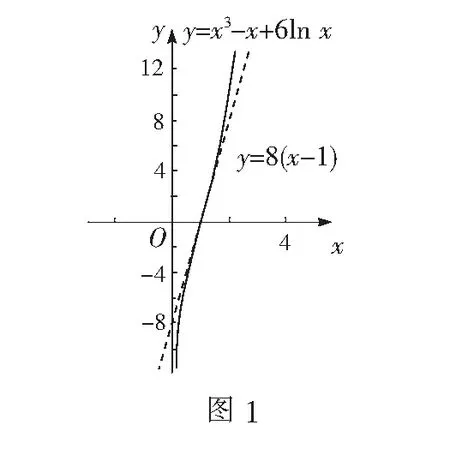
生6:函数f(x)在(0,+∞)上单调递增.

生7:f′(1)=8是f′(x)的最小值且点(1,0)是切线斜率变化的分界点.

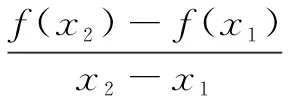
(生2在几位同学点拔之后,举手示意回答)

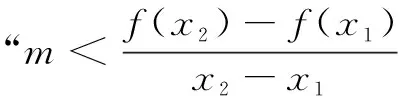
师:同学们的表现很好!你们在“将错就错”中寻找到正确的思路和解法,而且在整个过程中,同学们学会用所学的知识和方法去发现问题、分析问题及最终解决问题,并养成了敢于质疑、勤于思考、一丝不苟的优秀品质,这种品质对同学们会终身受益!

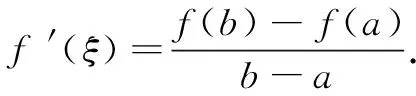
① 定理的几何意义:在满足定理条件的曲线y=f(x)上至少存在一点P(ξ,f(ξ)),使曲线在该点处的切线平行于曲线两端点所在直线;

② 定理中的包含关系:若满足定理条件的所有割线斜率记为集合A,曲线上的所有切线斜率记为集合B,则A⊆B;

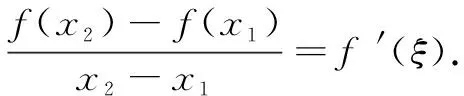
本题即为反例,事实上,存在拐点的单调函数均不满足逆定理.

案例2已知函数f(x)=x2lnx-a(x2-1),若当x≥1时,f(x)≥0恒成立,求实数a的取值范围.

生1:当x=1时,满足题意.

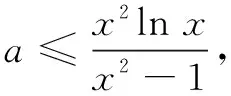
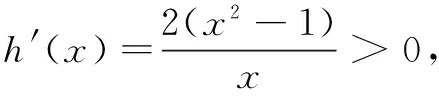
又因为h(x)>h(1)=0,所以g′(x)>0,即g(x)是(1,+∞)上的增函数.

……

师:怎么了?

生1:g(x)在(1,+∞)上单调递增,可是最小值g(1)无意义.(失落的表情)

师:可以通过逼近的思想求得函数g(x)在x=1处的极限值吗?