具有卫星厅的机场航站楼登机口分配研究

董 兵, 吴郑源, 赖桂瑾, 梁延安, 潘卫军

(中国民用航空飞行学院空中交通管理学院，广汉 618307)

据统计，2018年北京首都国际机场年旅客吞吐量突破1亿人次，而全国旅客突破千万级的机场增至37家。各机场航班量快速增长，导致了机场登机口不足，不仅使作业秩序变差，效率下降，机场航班安排受限，也降低了旅客的服务质量，制约了行业的健康发展。合理的登机口分配可以大大提高机场的运行水平，减少旅客步行距离，并提升旅客的满意度。为解决该问题，部分机场通过修建卫星厅的方式来提升飞机的靠桥率。由于候机楼和卫星厅通常会有一段距离，对本身已很复杂的登机口的分配问题，如何解决该类航站楼的登机口的分配问题已经成为机场运营亟待解决的关键问题。

登机口指派问题类似于停机位指派问题。当飞机无法停靠廊桥时，通常会被安排在远机位，通过摆渡车与候机楼建立联系。登机口指派问题一个NP(non-polynomial)难问题，通常有多个目标函数和约束条件，它的算法复杂程度随航班的增加成指数增长，短时间很难得到最优解。针对停机位指派问题，目前外国学者已提出多种分析方法。Jo等[1]、Brazile等[2]提出的专家系统方法通过将配置原则建立在知识库系统上，考虑了较多的非量化准则，但由于这类方法受搜索范围的限制，易忽视关键因素而导致分配结果不理想。此外，一些基于数学模型的方法，如Yu[3]、Yan等[4]所建立的模型以减少旅客的步行距离，减少未被利用的停机位数量，减少使用停机位的时间段范围为目标[5]，这类数学模型通常使用分枝定界算法，0-1数学规划、混合数学规划或网络流问题等数学方法对分配方案进行搜索优化，来给停机场机位分配提供方案，但在运算时间上不能够完全满足需要。由于受到目标函数的影响，会出现把较多的航班分配给较少的有吸引力的停机位，同时航班时刻的微小变化都会容易引起停机位分配的混乱和计算量的大增，降低了分配方案的鲁棒性。Zhu等[6]建立了一个以乘客步行距离最小和飞机的延误最小为目标的模型；李军会等[7]提出了基于贪婪算法的停机位分配方案；冯程等[8]提出了考虑滑行路径的分配方案。禁忌搜索(tabu search，TS)算法最早由Glover于1986年提出[9]，它是对局部邻域搜索的一种扩展。遗传算法(genetic algorithm, GA)是由美国Holland教授于1975 年首先提出的一种新的全局优化搜索算法[10]。GA算法具有内在的隐并行性，与其他优化算法相比，具有更好的全局寻优能力，但由于GA算法采用根据适应度的大小来决定个体是否被复制的选择机制，易出现来源于同一种群的个体被大量繁衍的情况，形成近亲繁殖，造成算法的局部搜索和过早收敛，从而导致全局寻优过程失败[11]。为了克服GA算法和TS算法的缺点，发挥它们的优势，针对新增卫星厅的机场，在参考已有文献的基础上，建立基于成功分配航班数最多、登机口使用数目最少以及中转旅客花费时间最短为目标的登机口分配的数学模型，采用遗传禁忌搜索(GA-TS)算法[12]，在解决航班能成功分配登机口数量最大的前提下，给出中转旅客最短流程时间之和最小的方案，以期得到满足机场实际运行需求的分配方案。

1 问题描述

考虑某机场在已有航站楼T的基础上，新增卫星厅S。航站楼T具备完整的国际机场航站楼功能，包括出发、到达、出入境和候机，而卫星厅S作为航站楼T的延伸，可以出发、到达、候机，没有出入境功能，机场布局如图1所示。

图1 机场航站楼T与卫星厅S的布局示意图Fig.1 Schematic diagram of layout of airport terminal T and satellite hall S

新增引入卫星厅后，缓解了原有航站楼登机口不足的压力，但对中转旅客的航班衔接具有负面影响。考虑登机口数和航班到离场时刻等条件下，加入中转旅客换乘因素，着手解决如何优化分配登机口，使得航班尽量多的分配到登机口，降低中转旅客的换乘紧张程度，并在此基础上减少登机口的使用数量，从而提高方案的鲁棒性。当加入中转旅客换乘因素，在换乘航班时需要有一定的时间来办理相关手续，将其定义为最短流程时间。由于航站楼T和卫星厅S不能直达，需通过捷运线连接(电车轨道)。乘客在候机楼中从廊桥到候机楼中心步行的时间由表1给出，最短流程时间和捷运乘坐次数如表2所示。

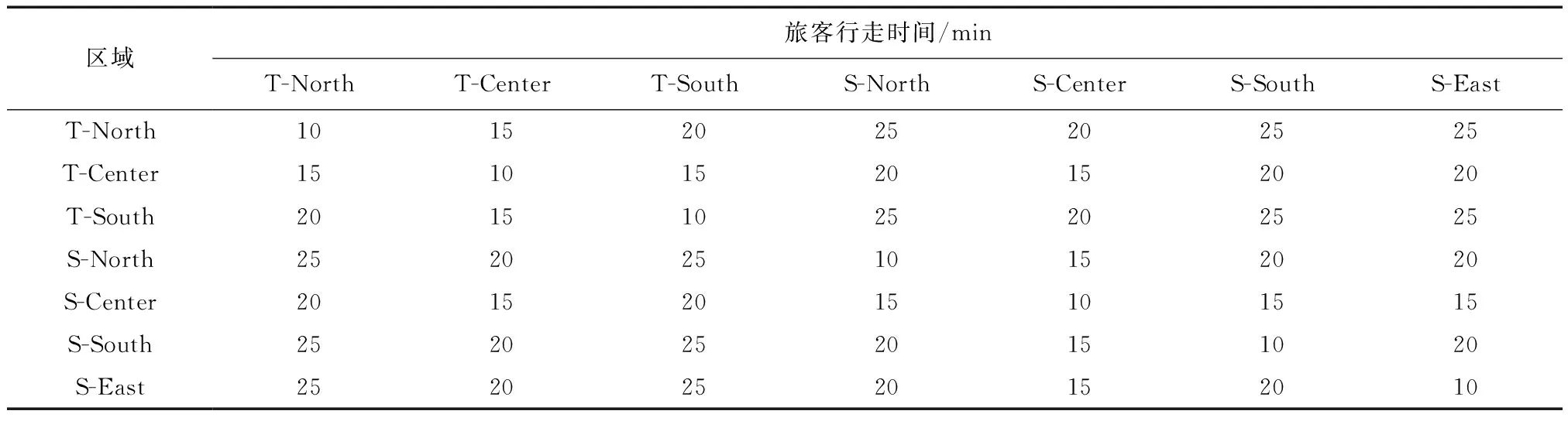
表1 旅客行走时间Table 1 Walking time of passengers

表2 最短流程时间及捷运线乘坐次数Table 2 Minimum process time and number of MRT rides

2 问题描述

2.1 问题的条件假设

为了方便问题的处理，需要对问题进行一些简化处理，具体如下。

(1) 航班的到达、离开，飞机的停靠、离开均按公布时间完成。

(2)飞机到达后，如没有分配登机口，则将该机停靠在远机位，此时摆渡车送人到航站楼或者卫星厅的时间可忽略不计，可认为飞机停靠在航站楼或者卫星厅。

(3)飞机一旦分配登机口，则一直占用登机口，不能移至其他登机口或临时停机坪，直到该机起飞。

(4)飞机占用登机口，到起飞离开后，占用此登机口时间机型按标准时间执行。

(5)有中转旅客的捷运时间和行走时间均以表1、表2为准，忽略个体差异。

2.2 问题的分析和建模

首先考虑约束条件：①飞机类型，需与登机口相匹配，大中型飞机不能被分配至小型登机口；②每个飞机只能分配一个登机口，或者不分配登机口；③分配到同一登机口的相邻飞机之间需要间隔45 min以上。

因此，模型具有三个目标函数，优先级从高到低。

(1)

式(1)中：Mij为航班-登机口匹配矩阵M的元素；ai为停靠登机口飞机类型；n为需要安排登机口的飞机架次，为当日的航班架次； 1≤i≤n；gj表示第登机口能够停靠飞机的类型；m为所有登机口数量，1≤j≤m。

飞机的集合为F，登机口的集合为G，F和G的笛卡儿乘积记作F×G，即，F×G={〈fi,gj〉fi∈Fandgj∈G}为飞机对应登机口有序对的集合。对于航班序列(f1,f2,…,fn)分配到对应的登机口(g1,g2,…,gm)，其有序对xi=〈fi,gj〉构成的序列x称为航班序列的分配方案。

根据假设构建登机口分配优化问题的数学模型，目标函数综合如下。

(1)航班分配数目标函数：

(2)

式(2)中:fi为0-1变量，表示第i架飞机是否分配登机口。

(2)最短流程时间和目标函数：

(3)

式(3)中：l为有效中转旅客组数；P为有效中转旅客集合，P={P1,P2,…,Pl}；Pk为0-1变量，表示第k组中转旅客是否成功转机；Tk表示第k组中转旅客最短流程时间。

(3)登机口使用数目标函数：

(4)

式(4)中：Gj为0-1变量，表示第j号登机口是否使用。

约束条件：

(1)Ai,j为0-1变量，表示航班-登机口实际匹配矩阵。飞机登机口类型匹配表示为

Ai,j≤Mi,j, ∀i∈n,∀j∈m

(5)

每架飞机至多安排一个登机口：

(6)

(2)飞机时间不允许冲突，即

(7)

(3)只考虑出发到达航班分配了登机口的旅客，得：

Pk=FAkFDk， ∀k∈m

(8)

式(8)中：下标Ak表示第k组中转旅客到达航班；下标Dk表示第k组中转旅客离开航班；引入其他变量的附加约束条件如下。

(4)飞机航班是否分配与实际分配间的约束表示为

max(Ai,j)≤Fi, ∀i∈n,∀j∈m

(9)

(10)

(5)航班-登机口实际分配与登机口的是否使用的约束表示为

max(Ai,j)≤Gj, ∀i∈n,∀j∈m

(11)

(12)

(13)

式(13)中：wf为航班因素权重；wg为登机口因素权重；wp为中转旅客因素权重。

根据多目标函数的处理方法，对不同优先级设定不同的权重。

(14)

(15)

3 模型的求解算法

式(14)、式(15)具有三个不同优先级的目标函数，属于多目标规划模型。由于数据量大，约束条件多，不易获得精确解，采用遗传禁忌搜索算法，以期求得较好结果。

使用GA算法和TS算法相结合组成GA-TS 混合算法，即以GA 算法为整个算法的框架，对GA 经过遗传操作运算后产生的新种群的个体，用TS 算法进行局部搜索，改善群体的质量。GA-TS 算法可以有效结合GA算法并行的大范围搜索能力和TS算法的局部搜索能力，其主要操作步骤如下。

(1)确定种群大小n，交叉概率pc，变异概率pm。

(2)通过先到先服务原则(first come first service,FCFS)，初始化种群：产生n组可行解组成初始种群p0。

(3)计算种群中个体的适应度值并进行选择操作。

(4)按照交叉概率pc、变异概率pm进行遗传操作。

(5)对GA 产生的新种群进行TS算法收索，改进种群个体的质量，产生新一代的个体。

(6)算法终止条件判断，如果满足终止条件，则输出最优解，算法结束，否则转步骤(3)。具体流程如图2、图3所示。

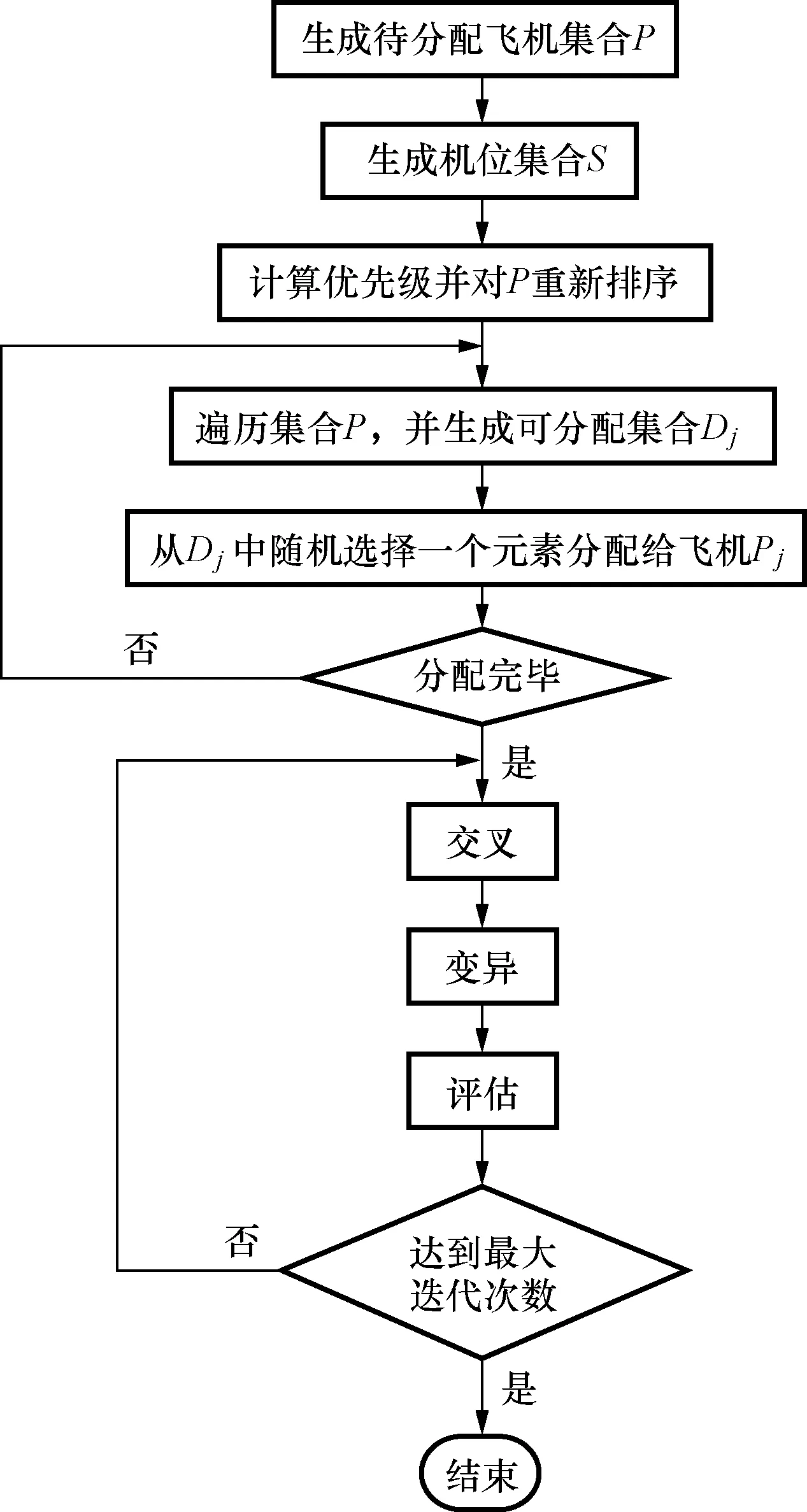
图2 基于遗传算法的机位分配流程图Fig.2 Flow chart of airport gate assignment based on GA

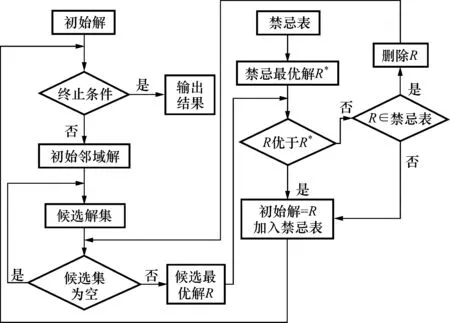
图3 禁忌搜索算法流程图Fig.3 Flow chart of TS algorithm

本文模型中，种群即为航班登机口分配方案，使用随机化的FCFS算法生成初始种群，种群大小为100。遗传运算中，交叉概率pc取值0.95，变异概率pm取值0.05，在计算适应度时，使用TS算法来改进种群个体质量，使得找到最优解效率有所提升。适应度函数fitness选取：

(16)

4 实例计算与结果分析

4.1 数据处理分析

数据来自某机场，其中航站楼T有28个登机口，卫星厅S有41个登机口。登机口的属性有：所在终端厅(T/S)、区域(North/Center/South/East)、能接受的航班到达类型(国际I/国内D)、能接受的航班出发类型(国际I/国内D)以及能停靠飞机的宽窄(宽W/窄N)类型。登机口属性不可修改，且只能接受航班到达类型、出发类型、机体宽窄类型以及适合的转场计划。

根据统计，当天的数据涉及303架飞机转场，1 649组中转乘客，69个登机口。表3仅列出了部分飞机转场数据，飞机转场数据包括：飞机转场记录号、到达日期、到达时刻、到达航班号、达到类型、飞机型号、出发日期、出发时刻、出发航班号、出发类型、上线机场及下线机场。限于中转换乘旅客数据较多，仅列出了部分中转数据。中转数据包含：旅客记录号、乘客数、到达航班、到达日期、出发航班、出发日期。飞机转场、登机口、中转乘客部分数据如表3～表5所示。根据机场航班登机口分配的要求，仅考虑20号到达或者20号出发的航班，数据中给出的时间均为年、月、日、时、分，为方便后期处理，统一将所有的时间全部转化为与2018年1月19日凌晨零时的时间之差。

表3 飞机转场数据Table 3 Data of the transferring aircrafts

表4 登机口数据Table 4 Data of the gates

表5 中转乘客数据Table 5 Data of the transferring passengers

根据假设，涉及的转场飞机、登机口数、有效中转旅客乘客组数分别为

(17)

4.2 计算结果分析

利用MATLAB程序对模型进行编程求解，模型求解部分结果如图4所示。

图4 航班-登机口分配甘特图Fig.4 Gantt chart of flight-gates allocation

(1)该模型能够给510个航班(255架飞机)成功分配登机口，占有效航班数的84.16%，其中使用了64个登机口，占可用登机口的92.75%；宽体机成功分配航班数为98个航班，分配成功率为100%，窄体机成功分配航班数为412，分配成功率约为81.10%。此时的有效中转旅客的最短流程时间之和为64 735 min，约合1 078 h。图4中为航班-登机口分配方案的甘特图，以及航班的具体分配情况，仅包含20日00：00—24:00数据。

(2)航班停靠了26个位于航站楼T的登机口，使用率为57.4%；航班停靠38个位于卫星厅S的登机口，使用率为61%。

(3)图5为以5 min为单位间隔的不同间隔时间段的中转旅客的概率及概率累计图。通过概率累计图来反映旅客中转的所花费时间，从而为降低中转时间提供了方向。

柱状图表示为每5 min为间隔的中转旅客的概率；折线图代表从0 min到当前 min概率累计图图5 中转旅客最短流程时间的所处时间段的概率及概率累计图Fig.5 Probability cumulative diagram of the shortest process time for transit passengers

5 结论

建立基于航班成功分配登机口最多的规划模型，客观合理地抽象了航班-登机口分配问题。在考虑中转旅客最短换乘时间的请款下，建立了在成功合理安排更多航班的前提下的中转旅客最短流程时间总和最少的规划模型。在求解过程中，采用了将遗传算法和禁忌搜索算法相结合互补的遗传禁忌搜索算法，得到了优化后结果。提出的计算模型对于计算航班-登机口分配方案仍有一些不足，例如模型并没有考虑旅客换乘航班为不同架次飞机的情况。在后期的研究中，应更多考虑机场的实际运营情况，还应考虑航班的动态进场和离场以及航班停靠和推出登机口时刻变动等因素。