斜撑支护体系在深厚淤泥区域基坑中的应用

刘晓玉, 黄 剑, 岳云鹏

(1.广州大学土木工程学院，广州 510006；2.国家知识产权局专利局审查协作广东中心，广州 510700)

进入21世纪以来，中国各大城市的经济和人口都得到了爆炸式增长。而建筑密度的加大，也更加考验深基坑支护技术对周边地表变形的控制能力。同时密集的建筑及地下管线等复杂的基坑周边地下环境，对深基坑支护形式也有很大的限制。考虑工期要求和经济成本因素，合理地选择最佳的支护形式和施工方案，将是一项非常有价值和现实意义的研究课题。斜撑支护体系由于其布置灵活、工期较短、造价低廉等优点被广泛应用的基坑工程中。

针对深基坑支护体系，中外学者做了大量研究，Addenbrooke[1]研究了基坑支护结构的位移柔度曲线，并对支护结构柔度指数进行研究；O’Rourke[2]等分析了在桩墙+内支撑支护形式下，基坑开挖引起的土体变形；史贵才等[3]对悬浮式水泥土框架支护结构的相关参数进行正交试验，确定了该支护结构在支护过程中的主要影响因素；杨博等[4]对格栅状地下连续墙进行试验研究，分析了地下连续墙的效应特征及变化规律；杨永新等[5]对土钉支护形式基坑在开挖过程中的变形及土压力进行研究，推导了考虑水平位移的土压力计算形式。一些学者[6-8]对基坑开挖过程中支护结构的变形进行数值计算，为不同地层中支护结构的选择提供依据。徐德馨等[9-10]分析了地表及基坑变形随开挖过程的变化规律，为优化施工方案提供参考；徐洋等[11]通过工程实例分析了不同支撑方案的优缺点及内力分布特点。

目前考虑斜撑支护体系的基坑支护形式研究相对较少。易奇雄[12]依据实际工程案例，介绍了一种新型斜撑支护形式，并推导出了斜撑水平及竖向承载力验算公式；宫喜庆等[13]介绍了使用盆式开挖加斜撑支护的施工工法，肯定了斜撑支护体系在减少成本及工期上的重要作用；唐浩[14]讲述了斜撑支护加中心岛开挖的施工流程及施工要点，充分论证了在大面积基坑中，斜撑支护体系独具的成本及工期优势；程胜一等[15]对钢支撑进行轴力测试,得到了应变计频率与支撑轴力的线性关系方程；刘燕等[16-17]、刘俊岩等[18]研究分析了斜撑体系的协同变形理论，推导了分区段拆撑长度的计算公式。

基于此，依据某工程实例，通过有限元建模模拟开挖工况，分别从地表沉降、桩体水平位移及斜撑轴力三个方面对计算结果进行分析，得出了斜撑支护体系在深厚淤泥区基坑中的变形及受力规律，相关结果可为未来的斜撑支护设计与施工提供参考及建议。

1 工程概况及基坑监测

1.1 工程概况

项目用地位于佛山市科技路南侧、天宇路北侧地块内，用地面积约67 369 m2，该项目塔楼距离项目围护结构约为47 m，该公馆住宅项目采用灌注桩承载形式。项目东侧为某在建地铁车站，距一期基坑最近距离105 m。采用分段组合支护形式。其中基坑紧邻绿荫路段距施工用地红线3 m，距路对面某公馆建筑的最近距离为47 m。基坑毗邻天宇路段距施工用地红线3 m，距天宇路外侧河涌40 m。基坑在天宇路与绿荫路交汇处向内凹进，该预留地块将用于售楼部建设。其余段为一期二期重合段，总长323 m。为保证基坑工程的安全性，同时尽可能地降低工程造价，本基坑支护设计根据不同剖面采用不同支护形式的分段组合支护方案，基坑位置及支护形式如图1所示。

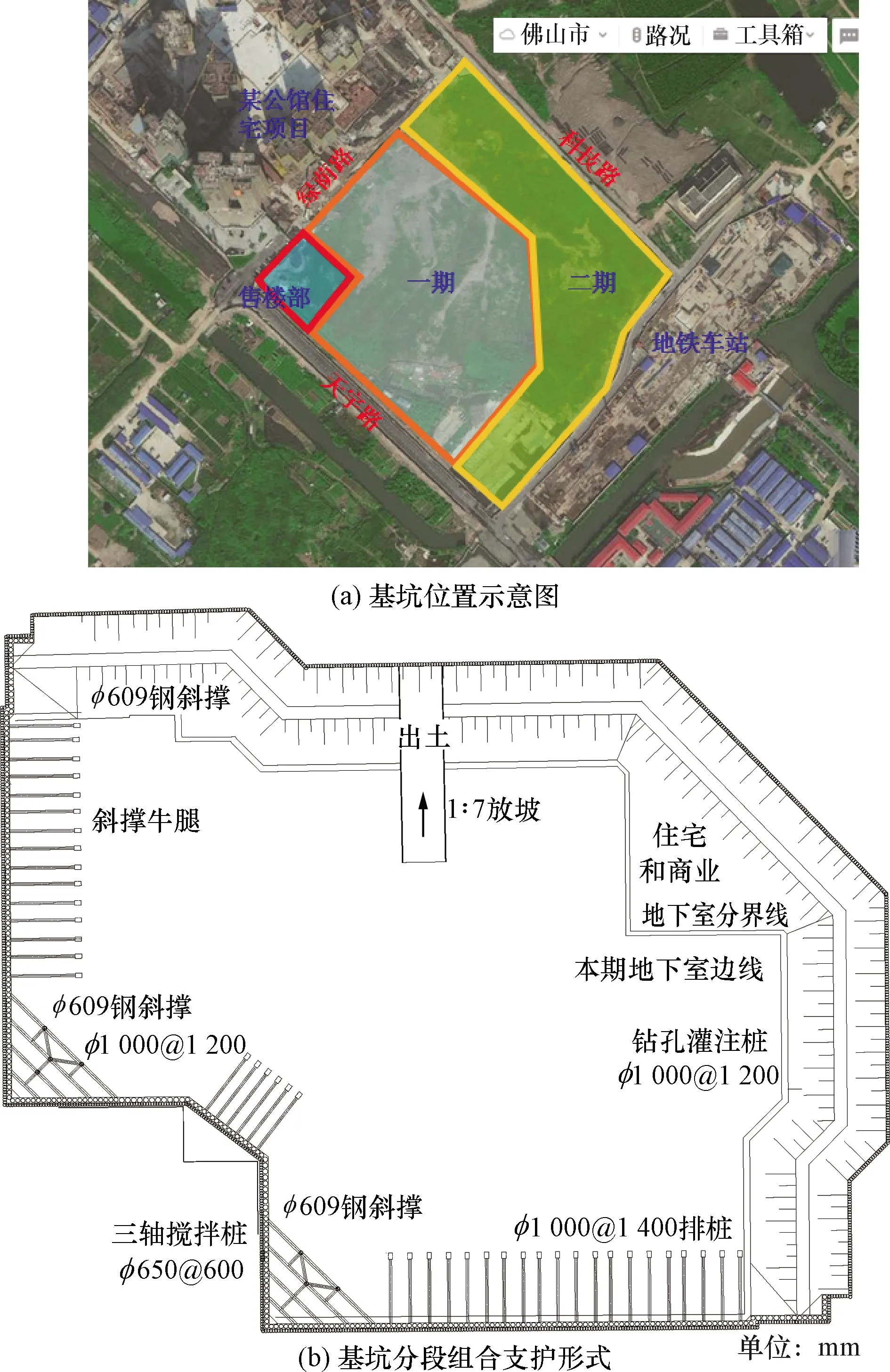
图1 基坑位置及支护形式示意图Fig.1 Schematic diagram of pit location and support form

1.2 基坑监测

研究的基坑工程监测项目主要有：围护结构水平位移及沉降观测、周边地表沉降观测、立柱沉降观测、地下水位观测、周边建筑物沉降观测、钢支撑轴力观测、土体深层水平位移观测、桩体深层水平位移观测，监测点布置如图2所示，根据实际监测情况需要可加大监测范围及增加监测点，基坑降水井数量可根据现场抽水试验适应进行增加或液少，在开挖前疏干待开挖基坑内的水后，再进行开挖，降水深度至地板地面以下0.5～1 m。

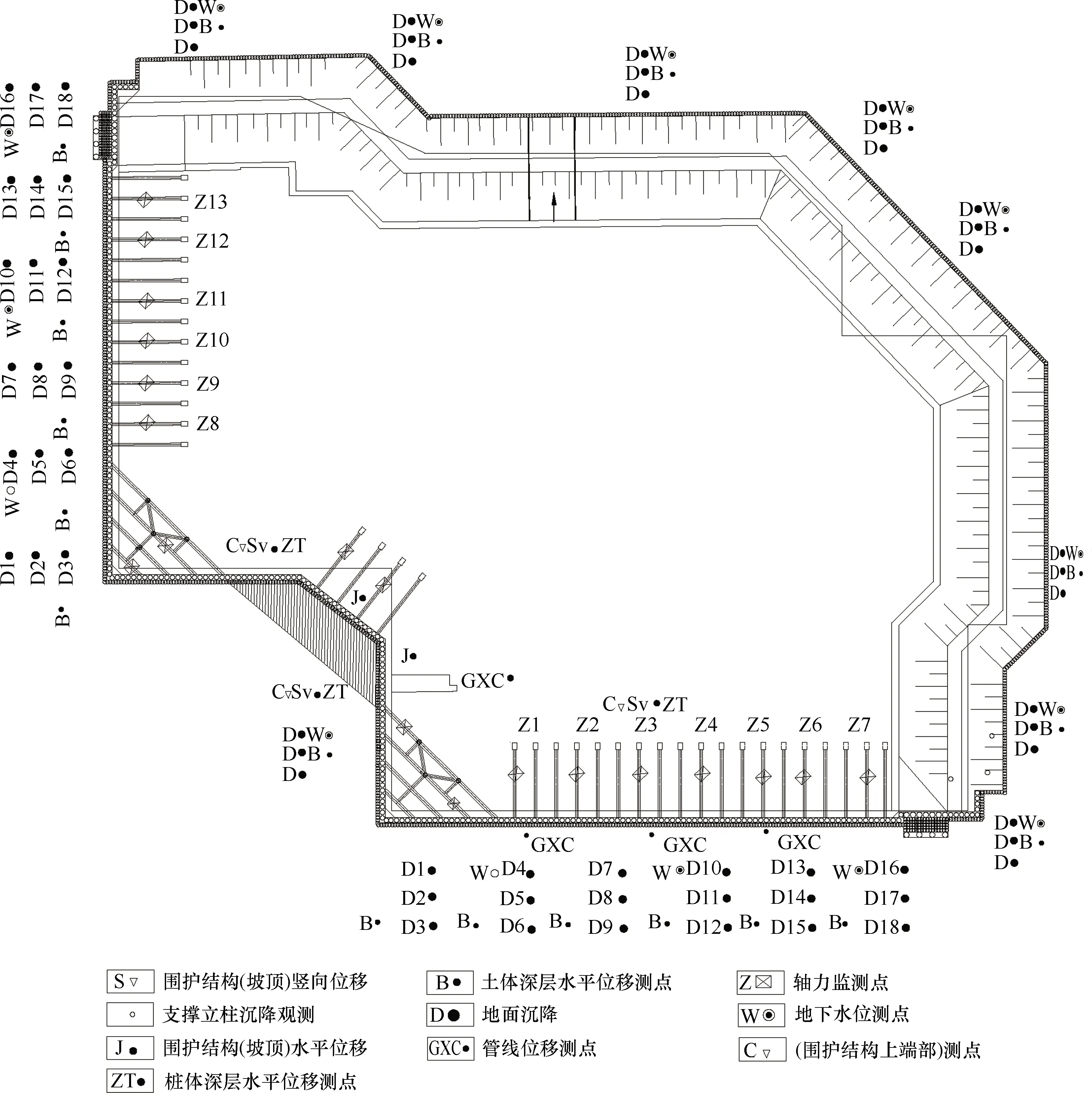
图2 基坑监测点布置Fig.2 Foundation pit monitoring point layout

2 模型建立

2.1 整体模型建立

利用MIDAS GTS NX中修正莫尔-库伦本构对模型进行建立，修正莫尔-库伦本构是基于莫尔-库伦本构进行完善后得到的本构模型，该模型可以较好地对卸载过程中土体刚度的变化进行模拟，且可以同时考虑压缩硬化与剪切硬化。修正莫尔库伦的主要参数有加载试验的初始刚度、三轴试验的切线刚度、卸载模量。该模型的剪切屈服面与莫尔-库伦本构是一致的，其压缩屈服面呈现为椭圆形的帽子本构。并且在修正莫尔-库伦本构中，对扁平面进行了圆角处理，消除了分析过程中产生的不稳定因素，使得运算收敛性更好。

通过前期固结压力与塑性应变对土体压缩硬化与剪切硬化进行等效模拟。

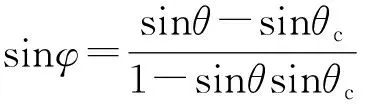
(1)

(2)

(3)

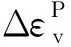
模型整体尺寸为180 m×120 m×40 m，基坑开挖范围为65 m×45 m，基坑开挖过程中土体处于卸载状态，现场卸载模量与土体的弹性模量接近。根据勘察报告及相关工程经验，基坑土层参数取值如表1所示。

表1 场地岩土层计算参数Table 1 Calculation parameters of ground rock and soil layer

2.2 支护体系参数选取

支护桩采用φ1 000@1 200的钻孔灌注桩，在有限元模拟中，往往通过刚度等效原则，将支护桩等效成地下连续墙来进行分析。研究经验表明，将支护桩等效成地连墙进行计算，是合理的，且其结果也比较安全。地连墙的厚度可利用等效公式求得。

为了更真实地反映现场基坑受力变形情况，主要构件斜撑采用1D梁单元进行模拟。根据设计方案，斜撑的布置跟地下室基础位置有关，其最大间距为4.5 m，最小间距为3.3 m，为简化建模过程，数值模拟中斜撑间距取值4 m。同时按照模型简化原则，斜撑一端的牛腿并不是研究重点，故不考虑牛腿的受力情况。而在模拟中，桩基采用植入式梁单元，从而使得模型更易耦合，提高计算效率。本模型支护结构计算参数如表2，按照现场位置关系建立模型如图3所示。

表2 结构材料计算参数Table 2 Calculation parameters of structural materials

图3 斜撑支护体系位置关系示意图Fig.3 Diagrammatic diagram of position relation of inclined brace support system

2.3 施工工况设置

基坑的支护与开挖施工是一个动态的、连续的过程，在进行数值模拟支护及开挖工况时，应尽量保持与现场情况一致。模拟设置的具体工况如表3所示，主要开挖工况的完成时间为：工况4开挖完成预计为2018年11月13日，工况5底板施工完成时间预计为2018年12月9日，工况6斜撑安装完成时间预计为2018年12月17日，工况7土坡开挖完成时间预计为2019年1月12日。

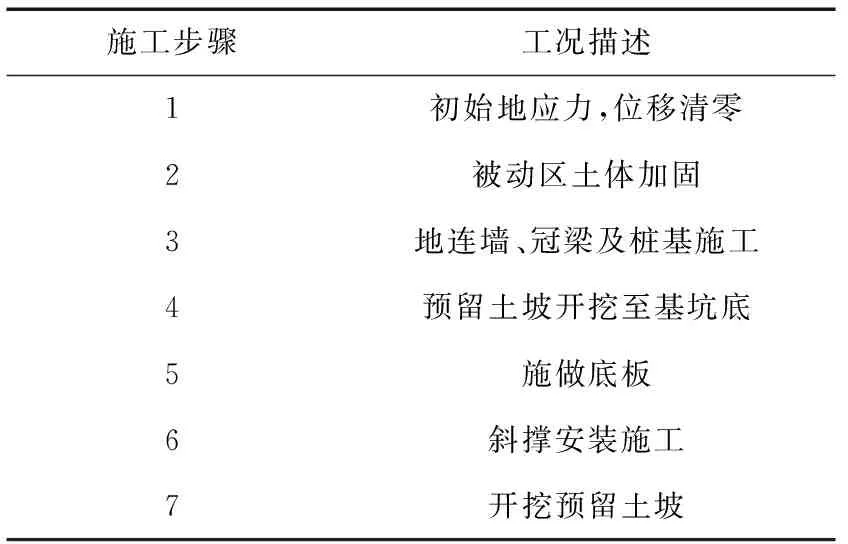
表3 工况设置Table 3 Conditions set

2.4 算例验证

基于以上参数及工况，选取桩顶水平位移监测点S18～S20的监测数据与工况计算结果进行对比，如图4所示。

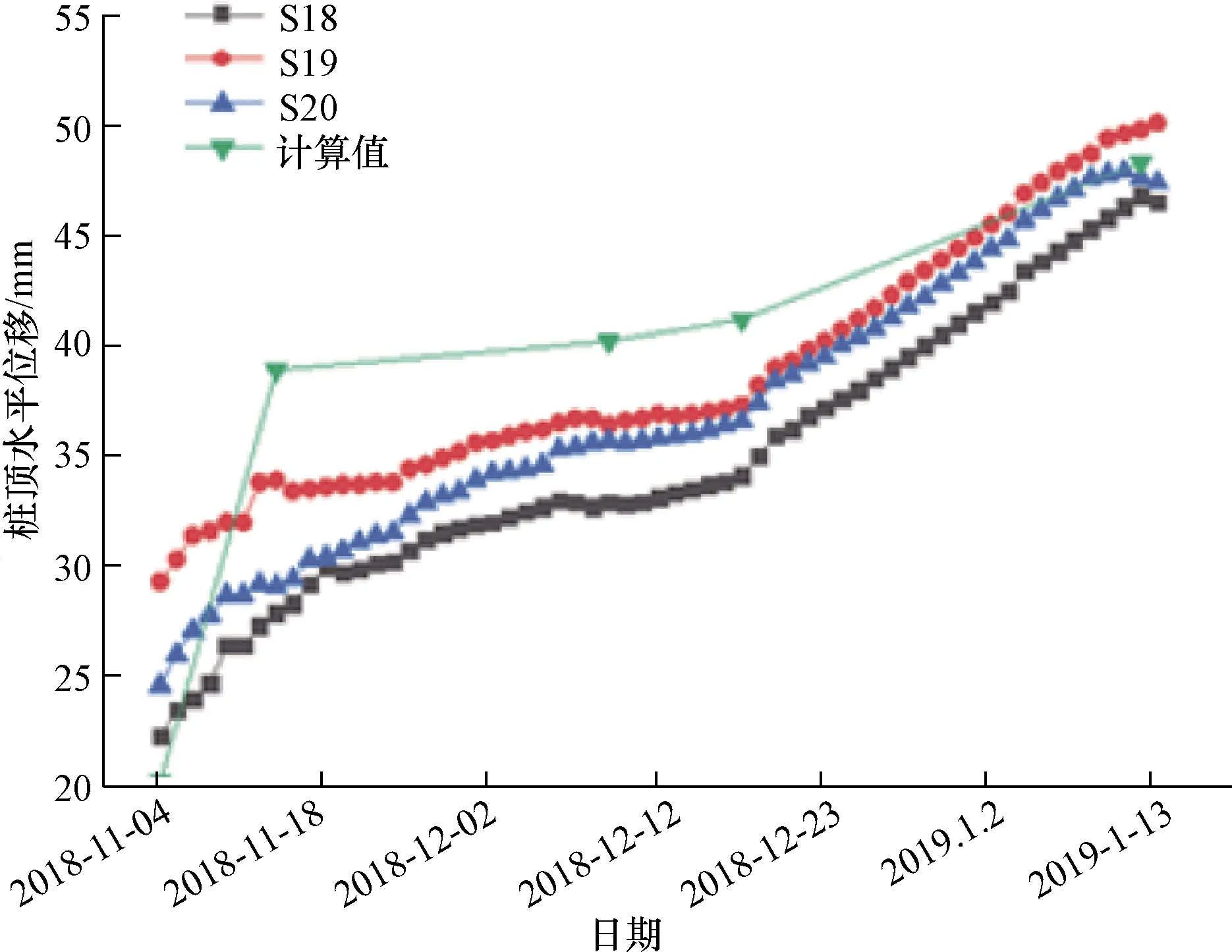
图4 S18～S20监测数据与计算结果桩顶水平位移对比Fig.4 S18～S20 monitoring data and calculation results of pile top horizontal displacement comparison

从图4可以看出，计算结果曲线与桩体水平位移监测曲线的变化趋势是一致的，且每个工况的位移增长斜率与监测数据较为相似。各个工况的计算结果基本大于监测数据的水平位移值，说明计算结果较为保守，本模型土层参数与结构参数取值合理，依此进行设计得到的支护结构也更为安全。

3 数值模拟计算结果分析

3.1 地表沉降数据分析

在斜撑作用下，分析工况4、工况5、工况6、工况7开挖过程中地表沉降规律，主要开挖工况对应的地表沉降曲线如图5所示。

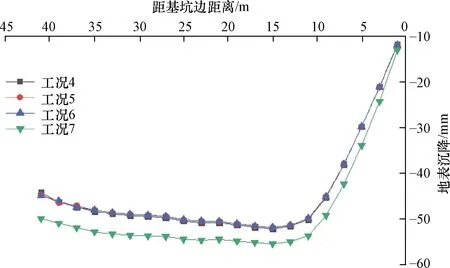
图5 开挖工况对应的地表沉降曲线Fig.5 Surface settlement curve corresponding to excavation conditions

从图5可以看出，4个工况的地表沉降曲线变化趋势一致，且工况4、5、6的地表沉降曲线基本重合，说明底板和斜撑的施工能有效控制地表继续下沉的趋势，而随着预留土坡的开挖，地表沉降量进一步增大。但在距基坑40 m处，4条曲线的地表沉降量依然较大，说明在深厚淤泥区，基坑地表沉降的影响范围较为深远。

选取距基坑边5 m处地表沉降监测点D34的监测数据与工况计算结果进行对比，如图6所示。

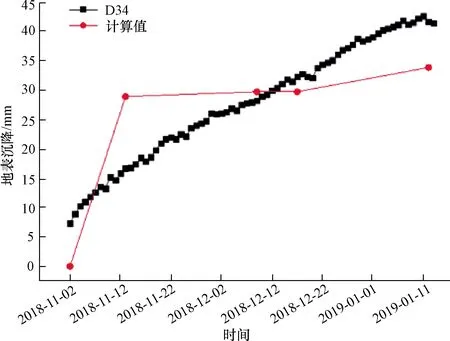
图6 D34地表沉降量监测数据与计算结果对比Fig.6 D34 comparison of monitoring data and calculation results of surface subsidence

从图6可以看出，计算结果曲线能较好地拟合地表沉降监测曲线的变化趋势，部分沉降量值与监测值相差不大，如工况5、工况6，但两次开挖工况的沉降与监测值相差较大，其中工况4计算结果较监测值大，而工况7小于监测值。可见，仅通过数值模拟并不能真实地反映现场地表沉降情况，在深基坑工程中对地表沉降进行监测是十分必要的。

3.2 桩体水平位移数据分析

主要开挖工况对应的桩体水平位移曲线如图7所示。

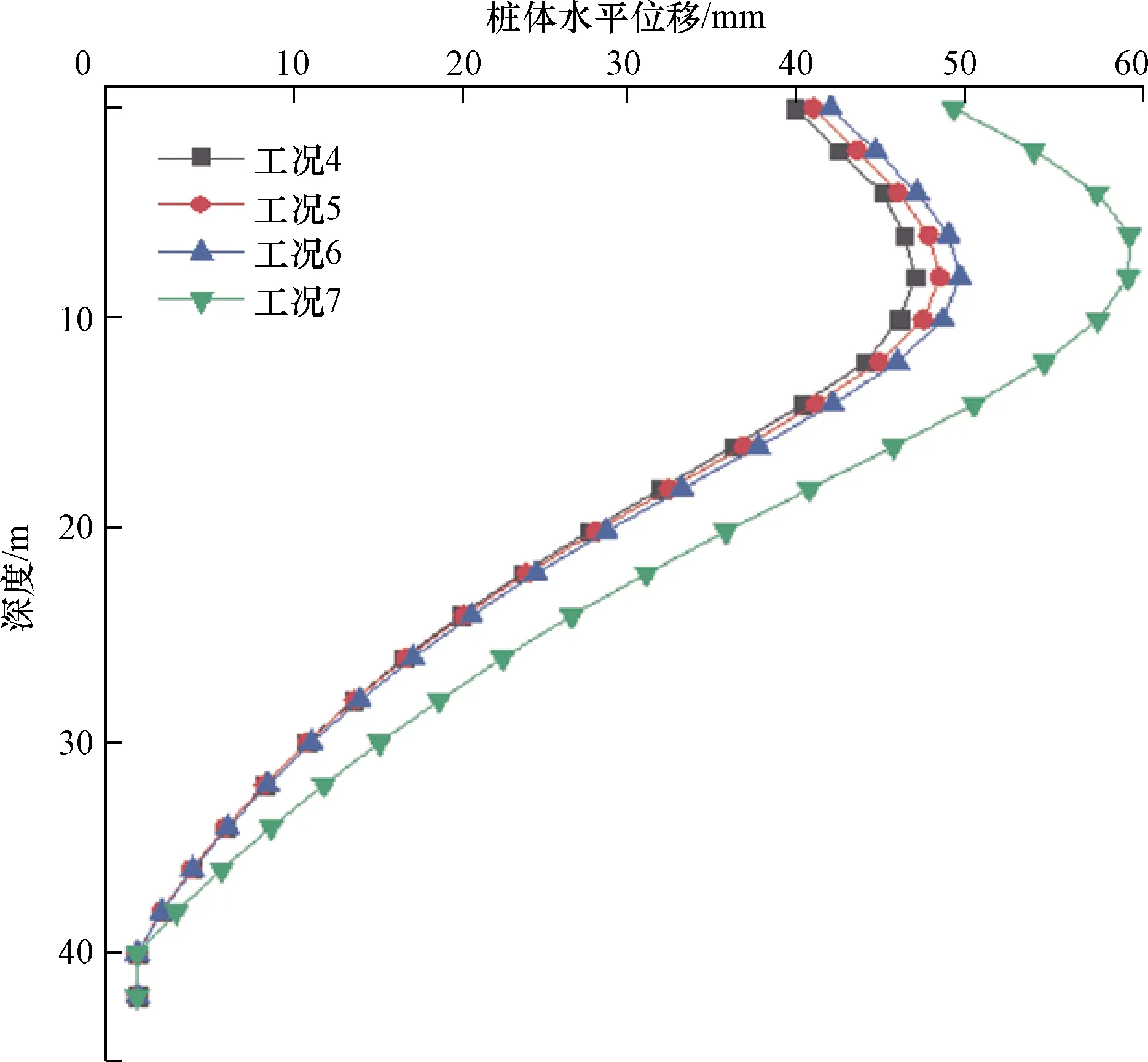
图7 开挖工况对应的桩体水平位移曲线Fig.7 Horizontal displacement curve of pile under excavation conditions

从图7可以看出，4条桩体水平位移曲线变化趋势相同，即桩顶有一段较大水平位移，但最大水平位移出现在基坑底下方1～3 m，超过位移最大值点，曲线(图7)随着埋深的增大逐渐收缩，在进入中风化砂岩土层后趋近于0。同时对比4条曲线(图7)可以看出，由于预留土坡的开挖，整个桩体的水平位移均有不同幅度的增加，且在斜撑的作用下，桩顶水平位移增量得到了有效控制。

3.3 斜撑轴力数据分析

数值模拟主要开挖工况斜撑轴力分布如图8所示。斜撑在基坑支护过程中承受压力。从图8可以看出，斜撑轴力最大值为 1 142 kN，出现在本支护段最左侧，斜撑轴力最小值为 1 089 kN，出现在支护段中间部位，且最大值与最小值相差53 kN。

图8 工况7斜撑轴力分布Fig.8 Axial force distribution diagram of inclined brace in working condition 7

4 斜撑支护体系单因素有限元分析

4.1 斜撑倾角变化对基坑工程的影响

建立斜撑倾角分别为15°、17°、19°、21°的四种工况对基坑变形的影响进行分析，不同斜撑倾角对应的坑底隆起曲线如图9所示。

图9 不同斜撑倾角对应的坑底隆起曲线Fig.9 The heave curve of pit bottom corresponding to different inclination angle of inclined bracing

四条曲线在斜撑支点处及桩基位置均出现了极小值，说明斜撑和桩基的存在对减小坑底隆起具有显著作用。处于斜撑支点与第二排桩基位置的土体隆起量受到了明显的约束作用，而在图9中坑底隆起曲线末端，斜撑倾角17°、19°、21°对应的曲线均存在巨大的隆起增量，这可能是因为第二排桩基与边界间的空间变大，从而出现了明显边界效应。仅从本图来看，斜撑倾角在15°时，其隆起曲线起伏情况较为均衡。

不同斜撑倾角对应的桩体变形曲线如图10所示。由图10可以看出，四种不同斜撑倾角的桩体变形都发生在基坑内侧，且桩顶有一段较大的水平位移，但最大水平位移发生在基坑底附近，之后随着深度的增加，桩体变形逐渐收缩直至趋近于0。四条曲线最大水平位移点所处深度依次为9、6、4.6、4.5 m，当斜撑倾角不断增大时，桩体最大水平位移值点由基坑底下方迅速向上移动，直至在坑底上方某一位置趋于稳定。当斜撑倾角在一定范围内时，桩体最大水平位移值随斜撑倾角的增大而增大，且增幅不断减小。而超出这一范围时，桩体最大水平位移出现了小幅度收缩。

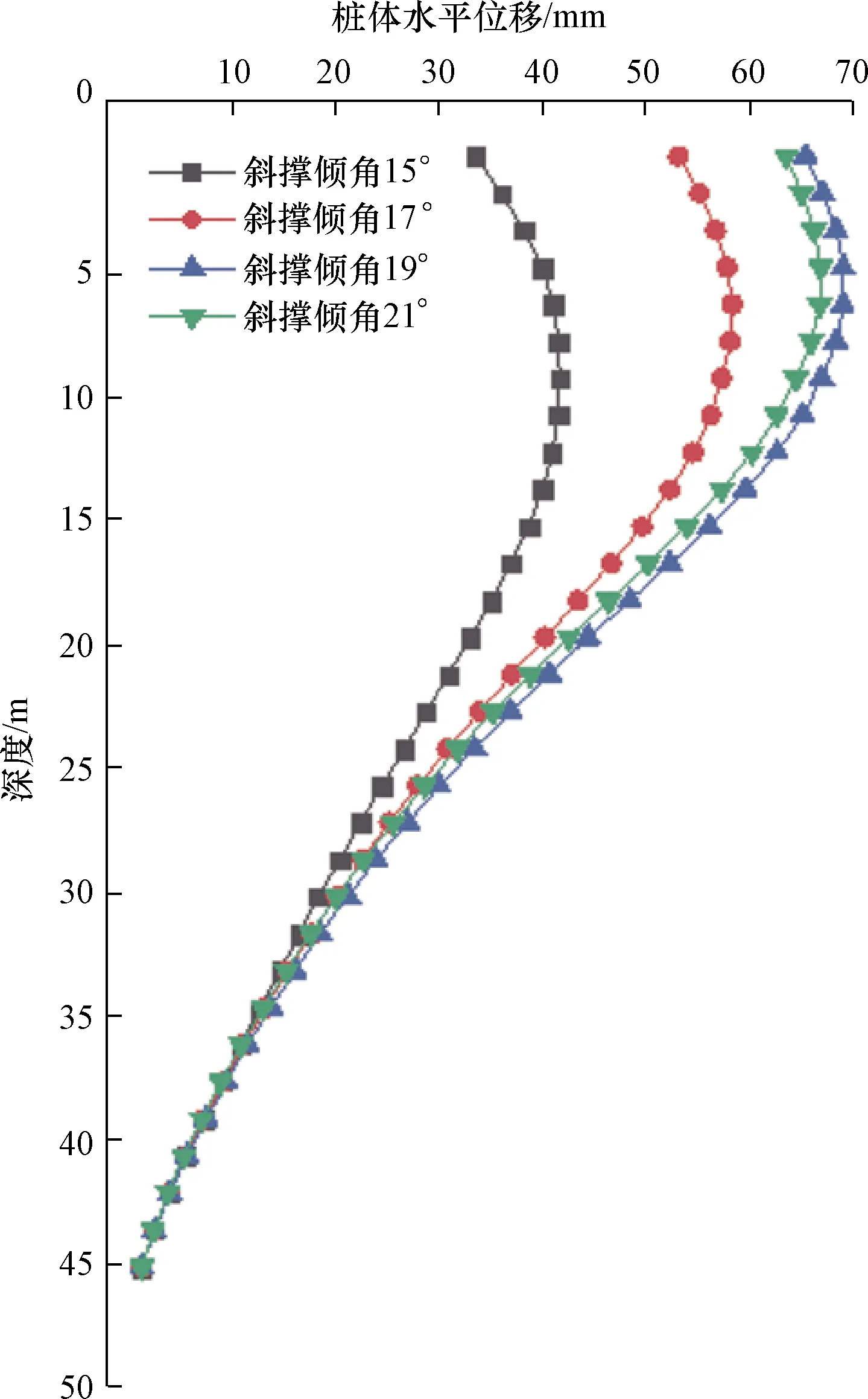
图10 不同斜撑倾角对应的桩体水平位移曲线Fig.10 Horizontal displacement curve of pile corresponding to different inclination angle of inclined bracing

4.2 斜撑间距变化对基坑工程的影响

固定斜撑倾角为15°，建立斜撑间距依次为4、5、6、7 m的四个工况，不同斜撑间距对应的坑底隆起曲线如图11所示。由图11可以看出，四条曲线几乎重合在一起，这说明斜撑间距对坑底隆起的影响微乎其微。

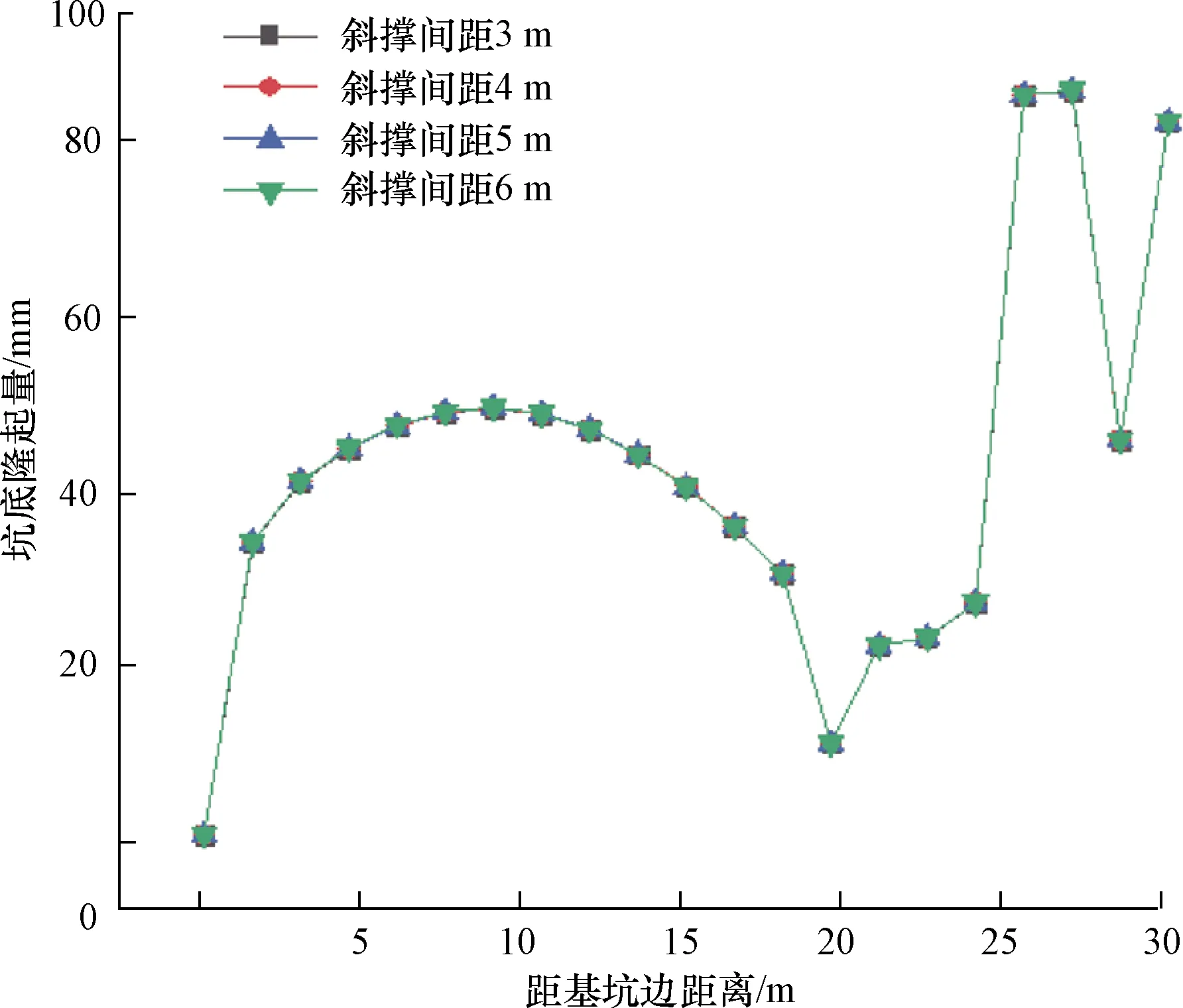
图11 不同斜撑间距对应的坑底隆起曲线Fig.11 The uplift curve of pit bottom corresponding to different diagonal bracing spacing

不同斜撑间距对应的斜撑轴力如图12所示。由图12可以看出，随着斜撑间距的增大，斜撑轴力大幅增长，且其增长斜率基本不变。

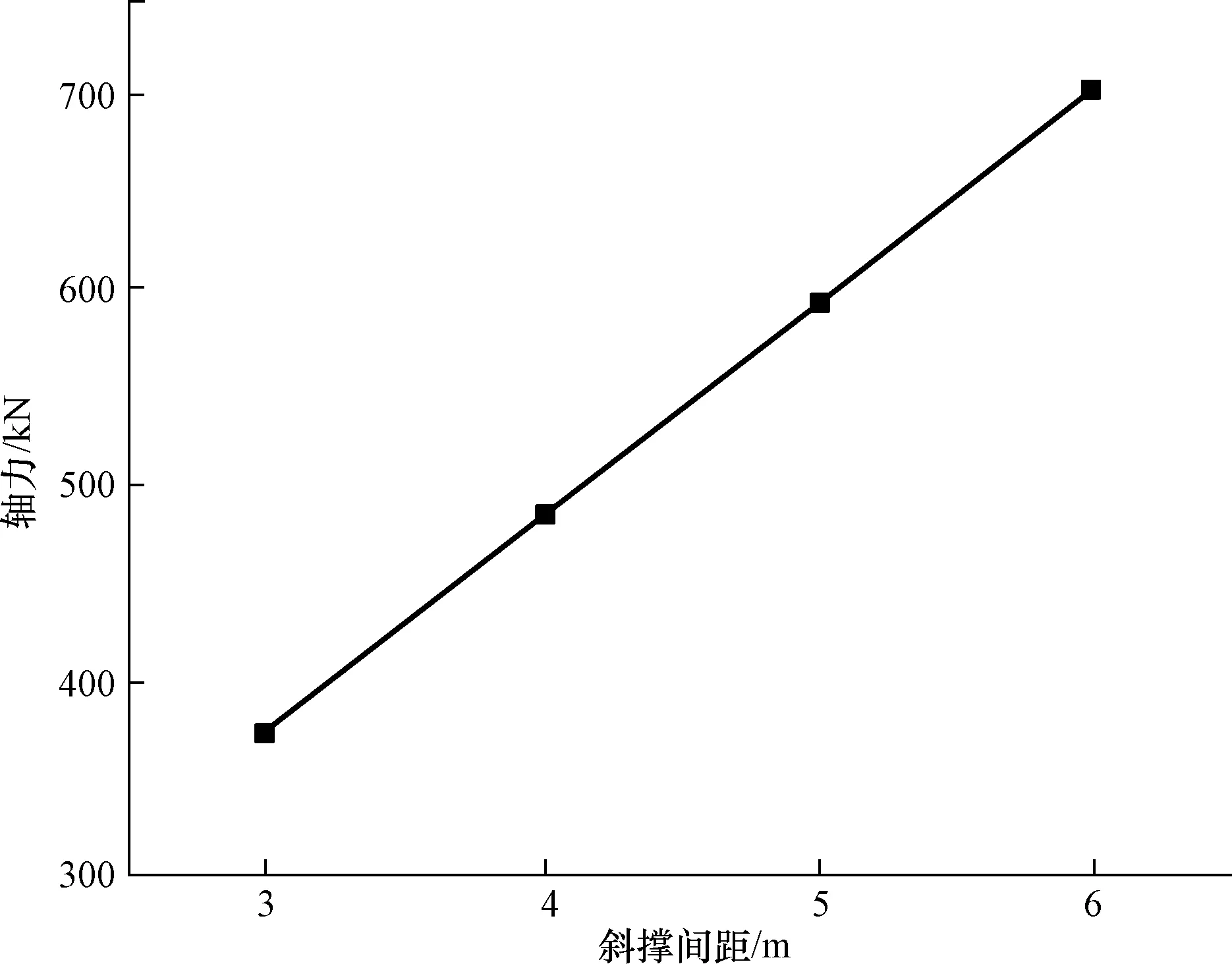
图12 不同斜撑倾角对应的斜撑轴力Fig.12 Axial force of inclined bracing corresponding to different inclined bracing inclination

5 结论

(1)通过监测数据与数值模拟计算结果的对比，得出了采用数值模拟能较好地拟合监测数据变化趋势这一结论。尤其是在桩顶水平位移的比较中，数值模拟计算结果略高于监测值，说明采用数值模拟方法来辅助基坑支护设计，得到的支护结构体系安全性更高。

(2)各个主要工况对应的地表沉降最大值位置发生在距基坑10～15 m处，最大桩体水平位移发生在距基坑底1～3 m，坑底隆起曲线在桩基及斜撑处均出现极小值。

(3)斜撑倾角增大的情况下，斜撑下方土体因为其距斜撑支撑点的距离更近，坑底隆起曲线有了明显的下降趋势。所以在确定斜撑倾角时，需考虑的因素较多，应权衡各方面变形及结构内力等因素，合理取值。

(4)斜撑间距变化对坑底隆起的影响不大，但斜撑轴力受其影响较为明显，且两者间呈等斜率线性增长趋势。

(5)在数值模拟过程中，并未考虑地下水及渗流的作用。而在深基坑工程领域，特别是在深厚淤泥区基坑中，这两者对基坑变形具有较大影响。如需更加准确的模拟基坑的完整变形，应该考虑地下水及渗流的作用。