基于核因子分析的捷联惯组稳定性评估技术

李 亚, 单 斌, 徐军辉, 甄占昌

(火箭军工程大学导弹工程学院，西安 710025)

随着惯性技术的快速发展，以及惯性导航不依赖外部信息的独特优势，捷联式惯性测量组合在航空航天、战略战术导弹及民用领域得到了广泛的应用[1]。稳定性是评价捷联惯组性能状态的重要作战指标，捷联惯组的稳定性是否合格决定了其能否被使用，但是受制造工艺、使用情况(通电时间、存储时间、温度、气压等)的影响，目前捷联惯组的稳定性较差。为了保证其使用性能，必须采用定期循环测试方案，且稳定性评估的结果仅有“稳定”和“不稳定”两项，存在太过单一、无法量化的缺点，不能给使用单位选用捷联惯组提供足够的信息支撑，极大地影响了捷联惯组的使用效率。

陈效真等[2]提出了一种利用大数据理论对惯组全寿命周期内的海量测试数据进行充分挖掘、分析与应用的数据分析平台的基本框架，但该框架中仅是一个雏形，其中数据挖掘、数据分析等关键技术还有待进一步展开深入的研究。当前，以惯组为主体进行状态评估的研究还比较少。但在旋转机械、机电设备等领域，基于数据驱动的状态评估已经得到广泛的应用。葛蒸蒸[3]等对弹上产品加速退化过程建模,然后利用方差-协方差矩阵研究了一种弹上产品的可靠性评估方法；陈建春等[4]利用时序主成分分析研究了捷联惯组的稳定性随时间序列变化的状况；邓超等[5]等基于维纳过程对某数控机床进行性能退化建模，然后用逼近理想解法和马氏距离实现了对该设备的健康状态评估。

因子分析(factor analysis, FA)[6]是主成分分析(principal component analysis, PCA)[7]的拓展，它与主成分分析最大的不同在于降维得到的各因子具有可解释性。利用同一批次，同一履历的捷联惯组在性能上相似的特点，改进了传统的因子分析方法，利用统计学习中的核化原理将其拓展为一种非线性特征提取方法——核因子分析(kernel factor analysis, KFA)，并基于核因子分析提取的特征进行了因子综合评价，实现了对捷联惯组的稳定性评估。基于KFA的捷联惯组稳定性评估方法流程见图1。

图1 基于核因子分析的综合评估方法Fig.1 Comprehensive evaluation method based on KFA

为了检验该方法的正确性和实际效果，推导了KFA中因子得分和因子载荷矩阵的求解过程，证明了KFA的合理性；利用K最邻近分类算法(K-nearest neighbor,KNN)[8]对基于KFA的捷联惯组稳定性评估结果与其他评价方法进行了对比，分析了其有效性和不足。

1 因子分析模型

因子分析的基本思想是通过分析多变量间的相关矩阵，找到支配变量间相关关系的少数几个相关独立的潜在因子，达到简化观测数据，用少数变量解释研究复杂问题的目的[9]。因子分析的一般模型为

X=AF+ε

(1)

式(1)中：X=[X1,X2,…,Xm]T为标准化的观测变量；AF称为公共分量，表示各个观测变量的共性信息；ε=[ε1,ε2,…,εn]为特殊因子分量，表示各个观测变量不能被公共因子解释的部分；F=[f1,f2,…,fr]T为公共因子向量；A=[aij]m×r为因子载荷矩阵，aij为变量Xi在公共因子fi上的载荷，它反映了公共因子fi对变量Xi的重要程度。

与主成分分析不需要假设条件不同，因子分析的一般模型基于以下假设[6]。

(1)E(F)=0,即各因子的均值为零，其中E表示均值。

(2)Cov(F)=E(FF′)=I，即各公共因子互不相关，其中Cov表示协方差。

(3)Cov(F,ε)=0，即各公共因子与特殊因子互不相关。

(4)E(ε)=0，即各特殊因子的均值为零。

2 核因子分析及稳定性评估

通过核函数使线性数据处理拓展到非线性数据处理的方法已得到广泛应用，典型的运用有核主成分分析、核独立成分分析、Fisher核判别分析等[10]。

传统因子模型的求解方法主要有极大似然估计法、主因子法和主成分法等，前两者都是基于相关矩阵求解的，但核空间中的相关矩阵不易求解；而主成分法既可以通过相关矩阵求解，也可以通过协方差矩阵求解。因此先用核主成分分析求解出原始观测变量在核空间中的主元，标准化后作为因子得分，再利用多元线性回归求出近似因子载荷矩阵用于解释各因子的意义，然后采用最大方差化方法进行因子旋转，求解旋转后的因子得分再进行综合评价。

2.1 基于KPCA的因子得分求解

假设Xm×n为一个经过标准化处理后的有m个变量、n个样本的“相关变量集”。将原输入空间映射到一个高维的特征空间F中进行因子分析。假设映射数据为零均值，则Xm×n经过非线性映射在F空间数据的协方差矩阵为

(2)

式(2)中：Φ(·)为进行非线性变换时使用的非线性映射函数。

假设协方差矩阵CF的特征值为λ，对应的特征向量为V，可得:

λV=CFV

(3)

将式(3)两边乘以Φ(xk)，式(3)可等价为

λ〈Φ(xk),V〉=〈Φ(xk),CFV〉,k=1,2,…,n

(4)

根据核再生理论，存在系数αi,使得CF的特征向量V可由Φ(xi)线性表示：

(5)

由式(3)、式(4)可得：

(6)

定义核阵K，令Kij=〈Φ(xi),Φ(xj)〉，则式(6)可以等价为

λnα=Kα,α=[α1,…，αn]T

(7)

令〈Vk,Vk〉=1，则

〈αk,λknαk〉=1

(8)

则样本的第k个主元为

(9)

由于在实际应用中映射数据为零均值的条件不是永远成立的，所以需要做如下式的中心化处理：

(10)

式(10)中：(1n)ij=1/n,(i,j=1,2,…,n)。

(11)

(12)

2.2 基于多元线性回归的因子载荷求解

所求fk为因子得分，由于映射数据的维数与大小是未知的，故F空间中的因子载荷矩阵A不可解。对这一非线性关系线性化，基于多元线性回归求解近似因子载荷矩阵。其关系式表达为

Xi=ui+(ai1,ai2,…,air)(f1,f2,…,fr)T+Δ

(13)

式(13)中:Xi为标准化的第i个观测变量；ui为截距；(ai1,ai2,…,air)为线性近似因子载荷矩阵的第i行；(f1,f2,…,fr)T表示样本在一定贡献率下各因子对应的因子得分；Δ表示残差。

主成分法确定的因子载荷不完全符合因子模型的假设前提，但当共同度较大时，特殊因子所起的较小，特殊因子之间的相关性所带来的影响几乎可以忽略[6]。当ui和ε很小时，忽略其对整体的影响，可以认为所提出的核因子分析满足因子分析模型的假设(3)～假设(5)。

多元线性回归本质上是利用最小二乘法使得残差最小，残差越小，拟合效果越好。所提出的近似因子载荷矩阵的拟合效果可以用模型的贡献率G表示，如式(14)所示：

(14)

式(14)中：p为观测变量的维数；r为因子数目;aij为近似因子载荷矩阵的元素。贡献率G越大时，残差越小，说明近似因子载荷矩阵解释的信息越多。

2.3 因子综合评价

因子综合评价是指以各因子的方差贡献率为权，由各因子的线性组合得到综合评价函数对样本进行评价的方法，表达式为

W=w1|f1|+w2|f2|+…+wr|fr|

(15)

式(15)中：wi为第i个因子的贡献率，fi为第i个因子的因子得分；W为综合评价结果。

fi实际上是各观测变量降维后的结果，它的绝对值大小反映了稳定性的大小，同时考虑到各个因子的贡献率之和不为1，不利于比较，取稳定性评价函数W为

(16)

3 实例分析

实验数据来自同一批次，同一履历的16套捷联惯组，剔除严重超差的测试数据之后，共有116组用于稳定性判断的数据，其中稳定的有84组，不稳定的有32组。考虑到不同误差系数的稳定性会随储存时间的变化而变化，故每组用于稳定性评估的数据为两次测试间的时间差和各误差系数(共33个)之差。使用的核函数为高斯径向基(RBF)核函数[11]:

K(x,y)=exp(-‖x-y‖2/σ2)

(17)

3.1 核参数的选择

高斯核函数只有一个可调参数σ，图2为提取核空间内原始数据最低贡献率85%时因子数目随σ的变化情况，它表明核因子分析的降维效果在特定样本总体下是有限的。

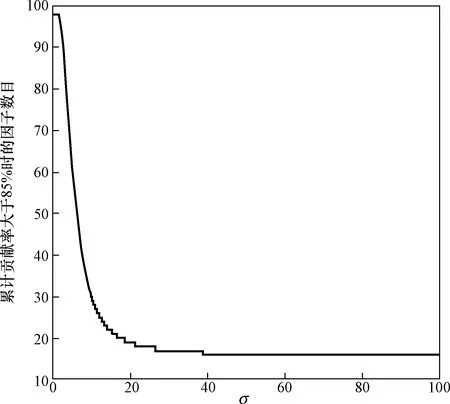
图2 最低贡献率为85%时的因子数目Fig.2 Number of factors with a minimum contribution rate of 85%

构建函数F(σ)=(sσ1+sσ2)/sb，sσ1、sσ2分别为稳定数据、不稳定数据核映射后的类内离散度，sb为两类数据核映射后的类间距离平方和，F(σ)可以用来表示一定核参数两类数据非线性可分程度。大量实验研究表明，在解决完全非线性可分的问题时存在着极小值点[12]。图3为F(σ)随着σ的变化，当σ取9.45时，F(σ)取得最小值，稳定数据与不稳定数据在核空间里最大程度非线性可分，但由于σ取较小值时降维后的因子数目较多，不利于解释各个因子的意义。选择因子数目为16，此时F(σ)最小时对应的σ为38.87。

图3 F(σ)变化曲线Fig.3 Change curve of F(σ)

3.2 因子解释

表1为部分的旋转成分矩阵。由表1可知，所提出的KFA方法降维后的各因子在方差最大化旋转后，具有较好的可解释性。

表1 旋转成分矩阵Table 1 Rotation component matrix

3.3 稳定性评价及结果分析

图4为所有样本的稳定性评价结果，其中前84个为稳定样本，后32个为不稳定样本。从图4可以看出，评分较低的主要是不稳定样本，但也存在一些不稳定样本的评分较高。

图4 KFA综合评价结果Fig.4 Result of KFA comprehensive evaluation

3.4 稳定性评估效果评价

为了对比提出的基于核因子分析的捷联惯组稳定性评估方法，将核因子分析与因子分析、熵值法两种方法进行了比较。采用KNN[13]这一经典分类算法分析不同的评估方法对于稳定样本和非稳定样本的的区分能力。为了取得相对稳定的结果，取100次十折交叉验证的平均正确率为指标；针对两类样本数目严重不均衡的问题，对算法中的投票原则[14]进行了调整使得其与两类样本的数目之比一致；KNN使用的距离量度为欧氏距离。

3.4.1 熵值法

熵值法[15]是一种绝对客观的赋权方法，它的评价过程完全依赖于客观的数据规律，从而很大程度上避免了人为因素的影响。

在熵值法中进行异质指标同质化时，采用负向指标进行归一化，即各误差系数的变化值越小，稳定性越好。

在熵值法中，第i个指标的权重为

(19)

式(19)中：di、Hi分别为第i个指标的偏离度和熵值。

3.4.2 结果分析

图5为原始数据-熵值法评估方法、因子分析评估方法(16个因子、贡献率为86.92%)、KFA评估方法(σ取38.87，16个因子，贡献率G为86.08%)的分类正确率比较图。在图5中，K大于30时3种方法的平均正确率都趋于稳定，并且在K大于60时平均正确率几乎一致；当K为30～60时，熵值法的评估效果要较好于KFA法和因子分析法，这是由于熵值法使用了原始数据，而其他两种方法在降维后失去了部分原始信息；KFA法和因子分析法的评估效果近乎一致，且都与熵值法的评估效果差别较小，这说明提出的基于KFA的捷联惯组稳定性评估方法是合理的。

图5 KNN分类结果Fig.5 Result of KNN classification

当K接近于交叉验证的训练样本数时，3种方法的分类正确率都逐渐稳定在77%左右。这是由于这3种方法都是只利用数据客观规律的方法，即稳定性评估效果最好的样本是样本总体里各观测变量变化最小的一个，但这并不能严格地与稳定性指标各个阈值的评价结果完全一致。

相对于熵值法不能用于降维的缺点和因子分析只能提取线性特征的不足，提出的KFA法具有能较好地提取原始变量的非线性特征并解释其含义的优点，比较适用于非线性关系较强的数据集。

4 结论

对捷联惯组的稳定性进行评估能更好地帮助使用单位了解捷联惯组的稳定状态，从而提高使用的效率。提出的基于核因子分析(KFA)的捷联惯组稳定性评估方法，从理论上证明了该方法能够满足因子分析的5个假设条件，并将其与熵值法和传统的因子综合评价方法进行了比较，证明了其有效性。

KFA方法的不足在于不能较好地与稳定性指标结合起来，将稳定与不稳定两种状态的捷联惯组完全区分开，实际上这也是熵值法等客观评价方法的共同存在的不足。下一步，可以将KFA法与其他主观评价方法结合起来，以取得更好的稳定性评估结果。