基于气动弹性载荷的电动飞机复合材料机翼结构优化及试验验证

李东辉, 杨凤田*, 马宏图, 邓立东

(1. 沈阳飞机设计研究所，沈阳 100135；2. 辽宁通用航空研究院，沈阳 110136)

电动飞机是当今通用航空发展的主要方向[1]。与油动飞机相比，电动飞机最大航时不超过1.5 h，最大航程小于350 km，在续航能力方面还有很多不足。影响电动飞机航程的主要因素包括电池能量密度、飞机升阻比、电池质量及推进系统效率等[2]。由于轻型运动类飞机有飞机总重的限制[3]，增加电池是提高其航程的方法之一，但这也对结构设计及质量控制提出了更高的要求。电动飞机机翼结构有两大特性：①现阶段电动飞机为提高升阻比，大多采用大展弦比机翼，因此机翼结构占全机质量比重较大；②电动飞机机翼内没有油箱，导致机翼惯性载荷相对油动机翼小[4]，因此翼根气动力与惯性力的合力及力矩比同重量级油动飞机大。由于上述特性，电动飞机机翼结构设计需根据精确弹性飞行载荷，对飞机机翼铺层优化进行研究，从而减轻结构质量对提升电动飞机续航能力有一定帮助。

文献[5]对大展弦比后掠机翼的气动载荷受静气弹效应影响进行了实验与分析，研究表明机翼刚度越低，后掠翼弹性机翼的载荷越低；文献[6]对复合材料后掠机翼的气动弹性剪裁方法进行研究，并归纳出提高机翼颤振速度的蒙皮铺层角度比例规律；文献[7]对复合材料无人机机翼结构进行优化设计，并通过静力实验进行验证。

前人研究主要集中在后掠翼的静气弹实验、复合材料机翼的气动剪裁设计、复合材料结构铺层优化及飞机静力试验等方向。 由于后掠翼机翼受气动载荷变形后，顺气流剖面的迎角减小，导致考虑气动弹性载荷的机翼载荷减小，为达到设计过载，总载荷相同，但靠近翼尖的气动载荷相对刚体气动载荷减小，因此机翼展向压心内移，从而达到减载的效果。后掠翼的静气弹特性，对机翼结构减重有着重要的意义。对于低速通用飞机，大多采用直机翼气动布局，机翼结构受气动载荷作用后，由于气动载荷弦向压心在机翼刚轴前，因此机翼会产生扭转变形，而该变形会增加局部翼型迎角，越靠近翼尖迎角变化越明显。在设计过载下，弹性机翼的气动载荷展向压心外移，导致翼根载荷增大，机翼刚度越低载荷越大。提高机翼刚度会减小气动弹性载荷的增量，但过度提高机翼刚度会增加结构质量，而过低的机翼刚度会使气动载荷增量加大，为满足翼根强度也会提高机翼结构的质量。基于RX1E-A电动飞机机翼对考虑气动弹性载荷的结构优化方法进行研究，通过合理的铺层控制机翼的刚度，从而达到机翼结构最轻的目的。

1 理论方法

1.1 优化设计方法

遗传算法由美国密执安大学教授Holland提出，通过模拟生物自然选择过程，保留适应度高的个体，寻求最优解的智能优化算法[8]。

机翼铺层优化设计过程中，由于轻型飞机翼肋铺层很薄，设计变量较少，因此翼肋铺层不作为设计变量。由于翼梁缘条仅承受轴向力，并且翼梁幅板及蒙皮属于薄壁结构，因此假设铺层顺序对层合板性能没有影响，但保证对称铺层。将翼梁缘条、翼梁幅板及机翼蒙皮沿展向分成n段，机翼蒙皮沿弦向分成n段，每段铺层厚度及0°、±45°铺层百分比作为设计变量。机翼蒙皮为泡沫夹心结构，泡沫厚度不作为设计变量。以实数编码创建种群，根据各染色体对应的机翼模型进行静气弹分析，强度及工艺性作为设计约束，以质量最小为设计目标。优化流程如图1所示。

图1 优化流程图Fig.1 Optimization flow chart

1.2 约束条件

1.2.1 强度约束

复合材料强度准则主要分为区分失效模式的准则(如Hashin失效准则[9]、Puck失效准则[10]及LaRC03失效准则[11]等)和不区分失效模式的准则[如极限强度准则[12](包括Max-Stress准则及Max-Strain准则)、Tsai-Hill强度准则[13]、Hoffman强度准则[14]及Tsai-Wu强度准则[15]等]。机翼结构优化过程中，通过Puck准则对结构强度进行判定。该准则能合理地模拟纤维间失效机制，且试验结果表明有很好的准确性[16]。

Puck准则区分了纤维断裂及纤维间破坏两种失效形式，除纤维拉压失效模式外，纤维间破坏模式又包括(Mode A、Mode B、Mode C)[10]。

纤维拉伸破坏模式损伤系数eft:

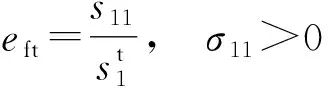
(1)

纤维压缩破坏模式损伤系数efc：

(2)

纤维间破坏Mode A模式损伤系数eModeA：

(3)

纤维间破坏Mode B模式损伤系数eModeB：

(4)

纤维间破坏Mode C模式损伤系数eModeC：

(5)

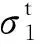
复合材料强度设计要求为极限载荷下不发生纤维破坏，限制载荷下不发生基体破坏。在Puck准则中纤维拉压破坏直接导致结构整体失效。Mode A失效模式为断裂表面彼此分离，在宏观表现为模量降低，而不会发生分层破坏。Mode B失效模式断裂面会挤压在一起，对于模量的影响不及Mode A。而Mode C失效模式为断裂面为斜面，破坏层与相邻层之间会发生分层破坏。因此在限制载荷下，不允许发生任何模式的破坏。限制载荷与极限载荷之间只允许发生Mode A与Mode B模式破坏，而纤维拉伸、压缩破坏及Mode C模式不允许发生。强度约束表示为

(6)

1.2.2 损伤容限设计约束

机翼结构损伤容限通过设计结构应变来进行控制。层合板最大拉应变为5 000，最小压应变为3 800，最大剪切应变为7 600。

1.2.3 工艺约束

为防止层合板的泊松比过大，层合板中各层角度所占比例为8%～67%。

1.3 气动载荷

机翼的气动载荷采用涡格法(VLM)计算。该方法将翼面延弦向、展向离散成有限个网格，每个网格布置强度为Γ的马蹄涡。马蹄涡又包括附着涡和自由涡，附着涡与网格的1/4弦线重合，自由涡则顺气流方向延伸到无穷远处。在3/4弦线的中点上布置有控制点，机翼的绕流在控制点处必须满足边界条件。利用Biot-Savart定律计算各个马蹄涡对控制点的诱导速度，根据边界条件解出马蹄涡的强度，进而求出与升力有关的气动系数[17]。机翼的气动网格如图2所示。

图2 涡格法翼面气动网格Fig.2 VLM aerodynamic grid

该机翼采用低速翼型，在使用涡格法计算气动载荷时必须考虑翼型弯度的影响。同时，翼面参数包括安装角及扭转角，因此各平板单元通过设置初始气动力下洗来实现上述机翼特性。下洗关系式为

(7)

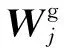
为验证考虑翼型弯度的涡格法计算的准确性，将缩比机翼模型分别进行CFD与考虑翼型弯度的涡格法计算，并将仿真结果及进行对比。CFD网格及压强分布如图3所示。

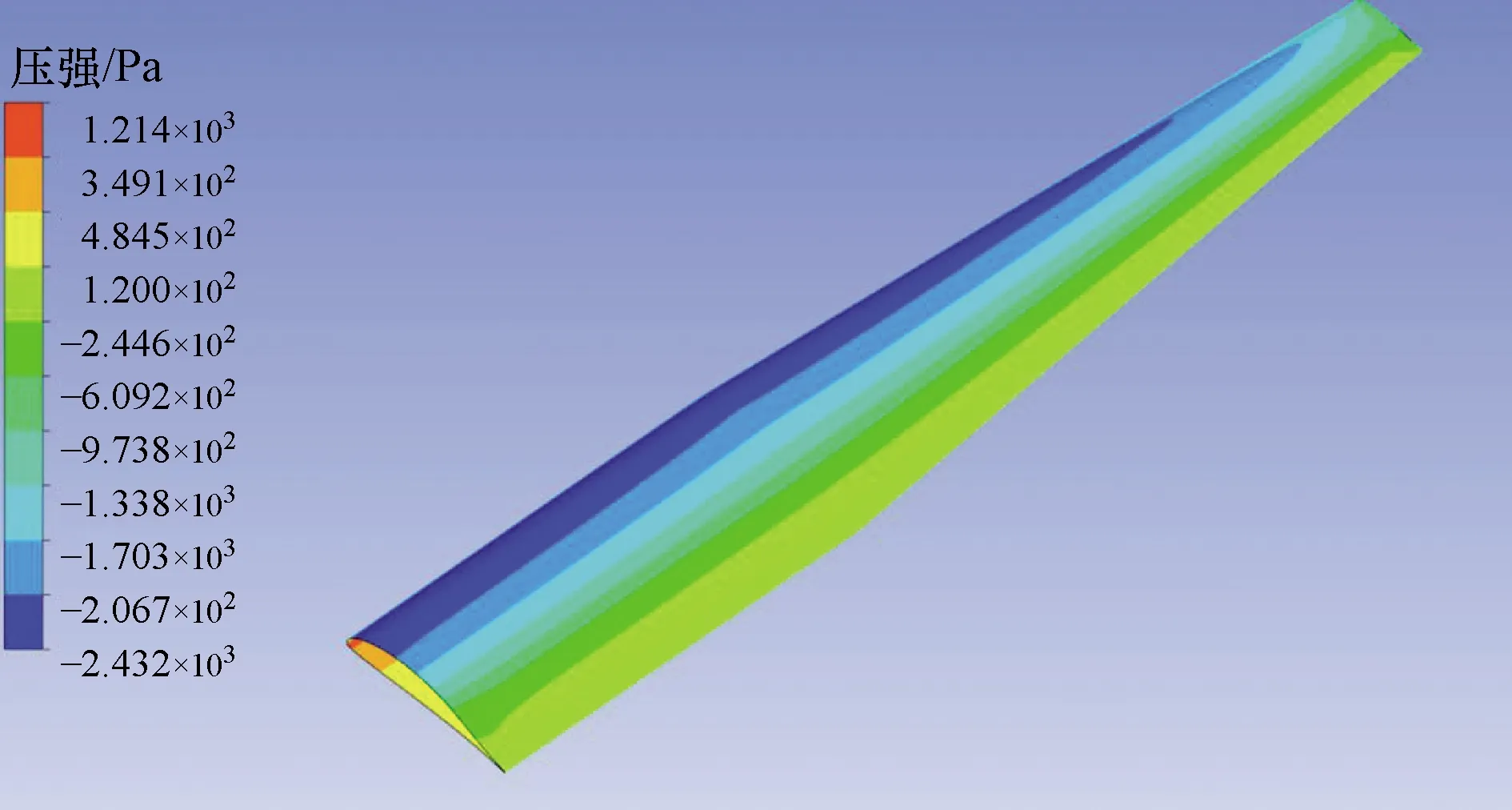
图3 CFD压强分布Fig.3 CFD pressure distribution

对比发现，涡格法最大升力系数误差为8.58%，俯仰力矩最大误差为5.5%。迎角-升力系数及迎角-俯仰力矩系数对比曲线如图4所示。

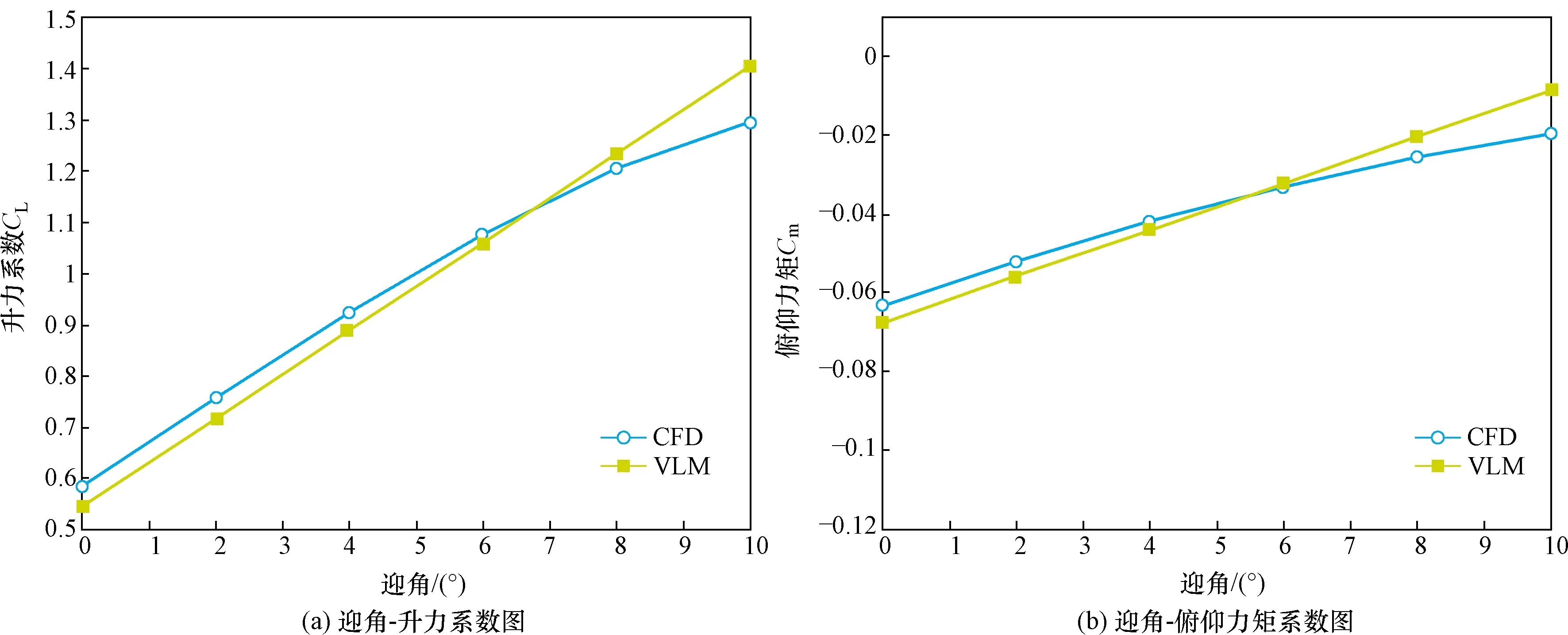
图4 CFD与涡格法升力机翼系数及俯仰力矩系数对比Fig.4 Comparison of aerodynamic data between CFD and VLM

10°迎角下载荷展向分布如图5所示。由仿真对比分析可知，考虑翼型弯度的涡格法计算结果能较好地与CFD计算数据吻合，可用于机翼载荷计算。

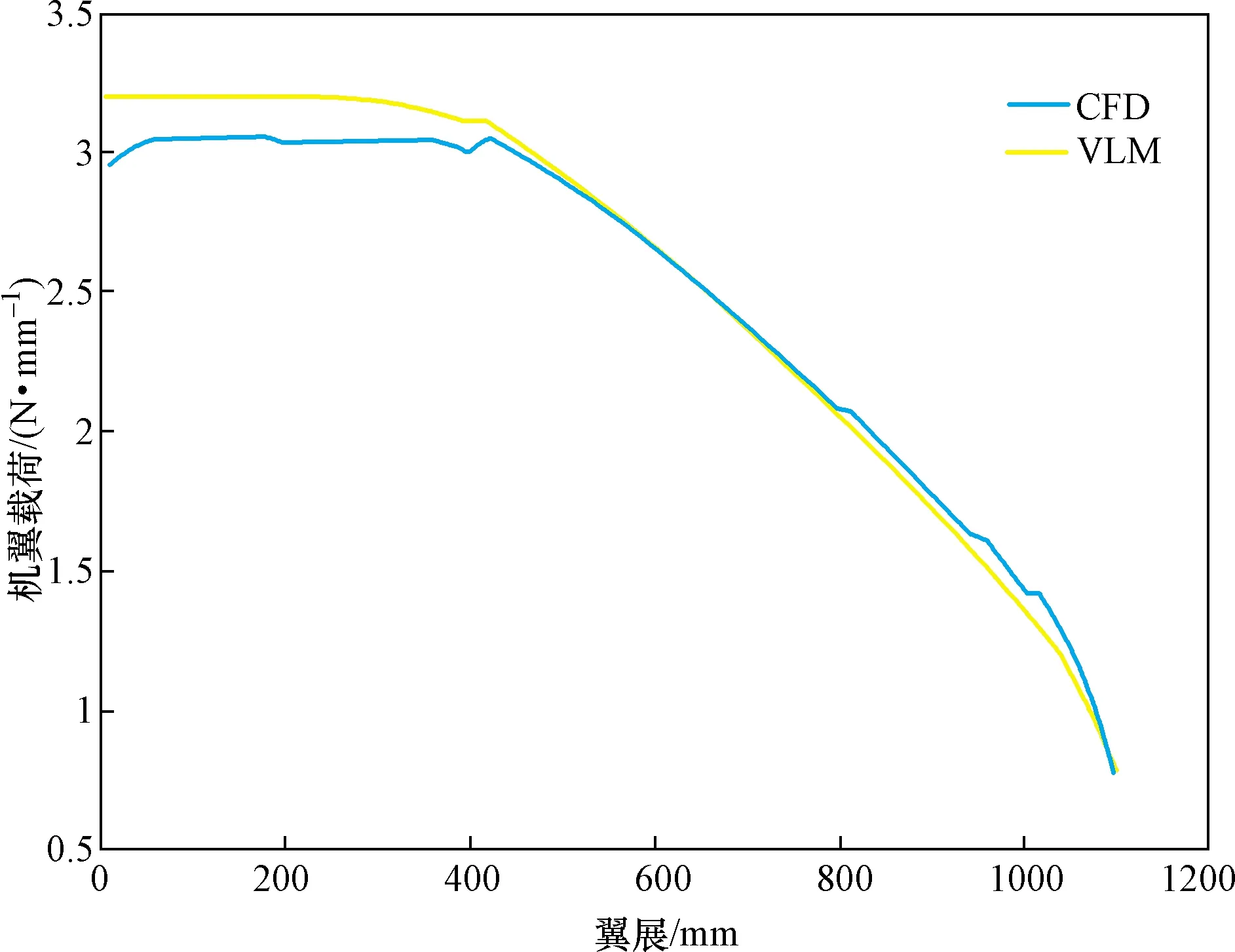
图5 CFD与涡格法计算机翼展向载荷分布对比Fig.5 Comparison of load distribution between CFD and VLM

1.4 气动弹性载荷对机翼结构的影响

RX1E-A飞机最大起飞质量600 kg，翼展为14.5 m，机翼面积为12 m2，最大过载系数为4，最大飞行速度为180 km/h。机翼采用单梁结构，展向分布10个肋，蒙皮为泡沫夹心铺层，泡沫厚度为4 mm，机翼结构仿真模型如图6所示。

图6 机翼结构仿真模型Fig.6 Wing structure simulation model

取最大飞行速度，过载系数为4的飞行状态，分别使用刚体载荷和气动弹性载荷对机翼结构进行仿真。限制载荷下，结构变形如图7所示。图7(a)为刚性载荷机翼变形，图7(b)为气动弹性载荷机翼变形，最大变形分别为 840、893 mm。载荷展向分布如图8所示，由于机翼的扭转变形，机翼剖面迎角沿展向逐渐增大，因此气动弹性载荷展向分布较刚性载荷大。翼根处载荷比较如表1所示，扭矩参考点为机翼刚轴，刚轴位置为38%翼型弦长。

图7 刚性载荷与气动弹性载荷作用机翼的位移Fig.7 Displacement of wing with rigid load and flexible load

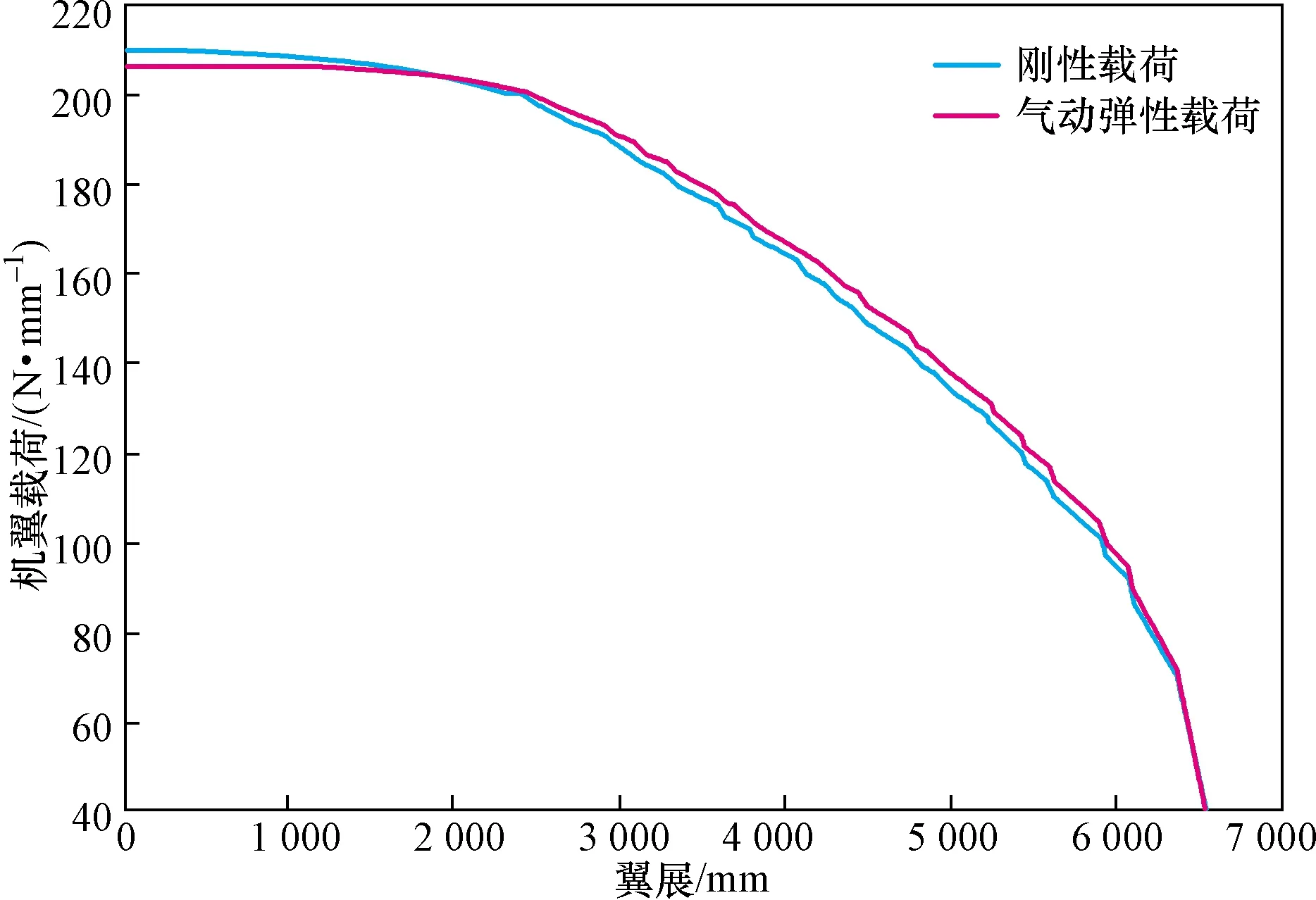
图8 刚体载荷与气动弹载荷延展向分布Fig.8 Distribution of rigid body load and flexible load of span

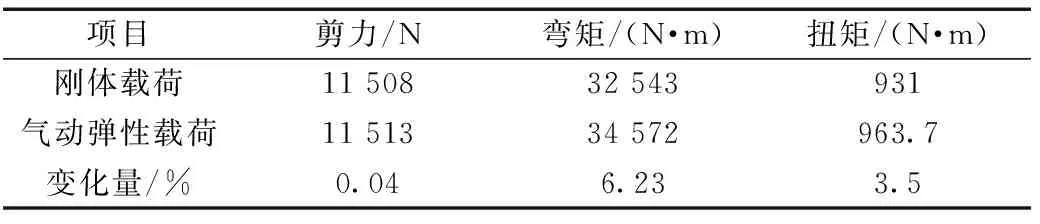
表1 翼根载荷Table 1 Load of root wing

仿真数据(表1)表明，直机翼结构承受气动载荷后，其弹性载荷为增量，限制载荷下弯矩增量最大为6.23%。因此在结构优化设计及试验验证中，应考虑载荷弹性载荷的影响。

2 优化仿真结果对比分析

2.1 优化结果

原机翼结构按照刚体气动载荷设计，结构刚度未作为设计约束，因此考虑气动弹性载荷后，由于弯矩及扭矩增加，结构强度不满足设计要求。将结构进行局部补强，确保考虑气动弹性载荷载荷后结构能够满足强度要求。补强后结构质量为33.79 kg。补强后结构作为优化前结构构型。

经过120代进化后结构质量基本稳定。机翼质量进化过程如图9所示，优化后Puck准则各破坏模式如图10所示，纤维拉伸破坏模式损坏系数为 0.951 2<1；纤维压缩破坏模式损坏系数为0.995 5<1；Mode A模式损坏系数为0.936 1<1；Mode B模式损坏系数为0.483 2<1；Mode C模式损坏系数为0.663<1。由上述参数判定结构满足设计强度要求。

图9 机翼结构质量进化Fig.9 Evolution of wing structure weight

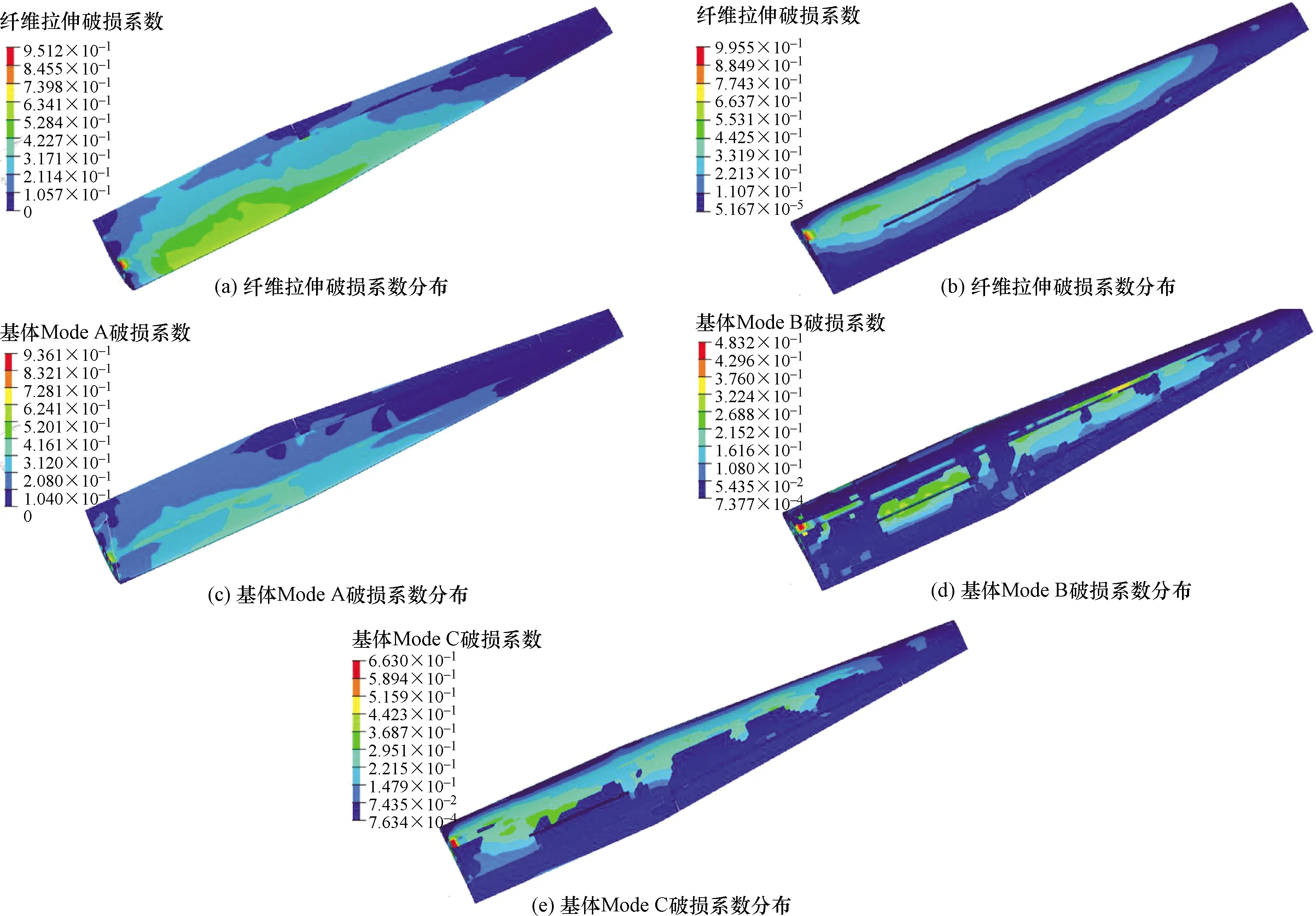
图10 Puck失效模式Fig.10 Puck failure mode

2.2 对比分析

机翼变形图如图11所示，优化前机翼极限载荷下最大变形为1 337 mm，翼尖扭转角为3.17°[图11(a)]；优化后最大变形为1 245 mm；翼尖扭转角为2.02°[图11(b)]。由图11可知，优化后机翼刚度有所提高。机翼载荷变化如下：翼根弯矩相对原载荷减少4.33%，扭矩减少2.72%。优化后结构刚度提高，导致弯矩、扭矩载荷降低，，因此机翼结构优化后质量为32.19 kg，减重4.74%。优化前后结构变化如表2所示，t表示该区域层合板厚度，P0°表示0°铺层厚度占该区域总厚度的百分比，P±45°表示45°铺层厚度占该区域总厚度的百分比。

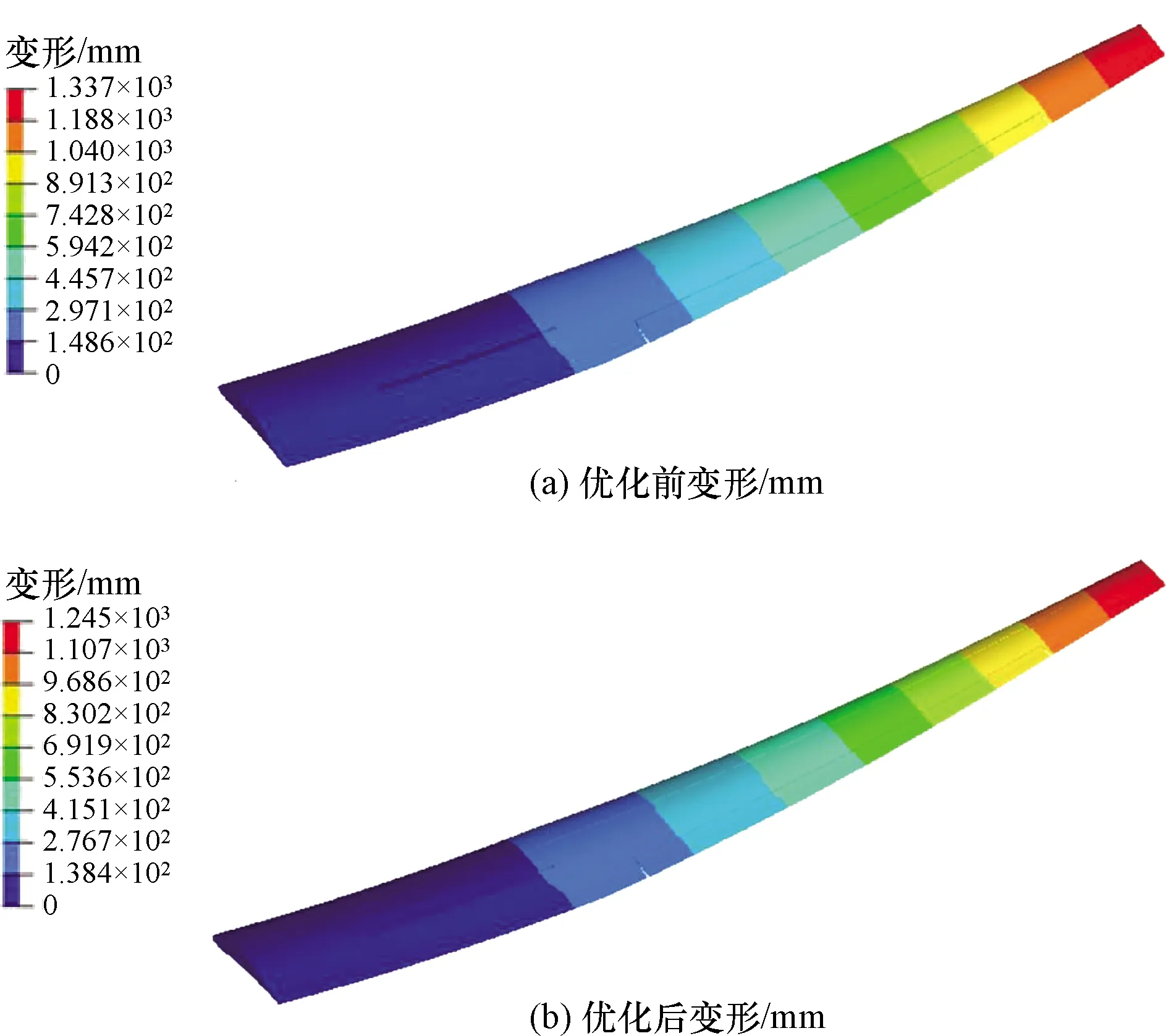
图11 机翼变形对比Fig.11 Comparison of wing deformation

表2 结构优化数据对比Table 2 Structure optimization data comparison

3 试验验证

3.1 试验方案

对于轻型通用飞机机翼静力试验，由于载荷较小，为降低成本，通常采用沙袋加载。试验为单侧右机翼加载，为防止台架倾覆，将左侧机翼简化成梁结构，根据载荷展向压心确定梁长度，在梁端施加平衡载荷，试验方案如图12所示。施加载荷考虑弹性载荷，并将载荷沿机翼展向分成10个加载区域。加载弦向位置为载荷弦向压心，试验过程中将沙袋放在载荷压心处。

图12 试验方案Fig.12 Experiment plan

试验过程中，依次以30%、50%、67%(限制载荷保持30 s)、75%、80%、85%、90%、95%、100%(极限载荷保持3 s)极限载荷加载。极限载荷后再通过每次5%极限载荷增量继续加载直到结构破坏。

机翼结构上下蒙皮翼梁位置分别沿展向粘贴应变片(s1、s2、s3、s4)，位置如图13所示，试验过程中实时监测结构应变。翼尖处分别在翼型前后缘处测量变形量，并通过差值计算机翼扭转角。

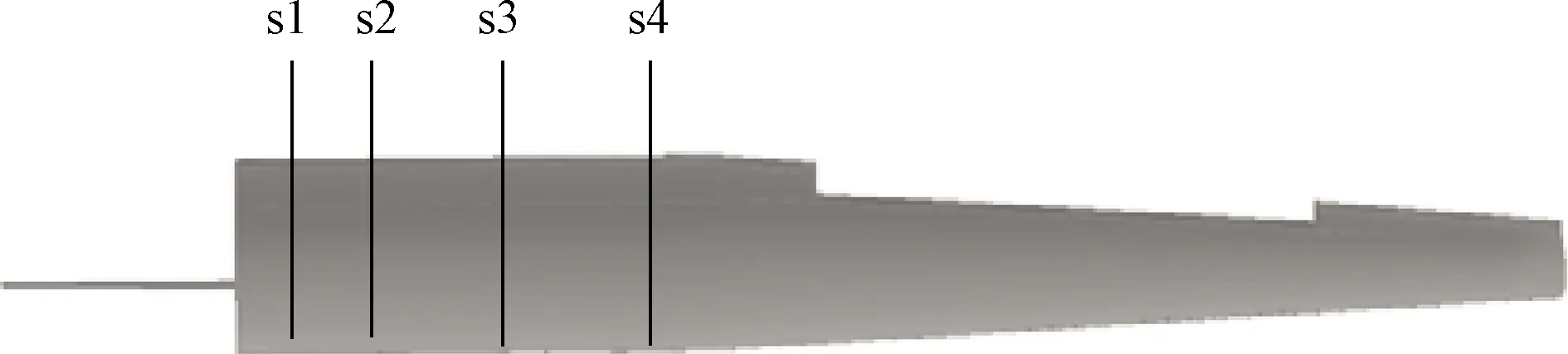
图13 应变片位置Fig.13 Location of strain gauge

3.2 试验结果

载荷由30%分步增至67%极限载荷后维持30 s，整个过程结构未发生异响及破坏，应变测量值在安全范围内，限制载荷加载状态如图14所示；载荷增加到100%极限载荷并维持3 s，过程中局部有开胶异响，但对整体结构没有影响；当载荷增加到110%～115%时结构发生破坏，结构破坏如图15所示。

图14 限制载荷机翼静力试验Fig.14 Wing static experiment of limit load

图15 机翼结构破坏Fig.15 Failure of wing structure

3.3 试验数据对比分析

极限载荷下仿真结果与实测应变对比如表3所示，实测最大拉应变位置为下表面1号应变片，为 4 733；最小压应变位置为上表面1号应变片，为-3 678；最大理论误差为15.59%，为下表面4号应变片。实测翼尖最大位移为1 142 mm，理论计算误差为9.02%。实测最大扭转角为1.63°，理论计算误差为24%。机翼结构加载到115%极限载荷时发生破坏，强度计算误差为15%。

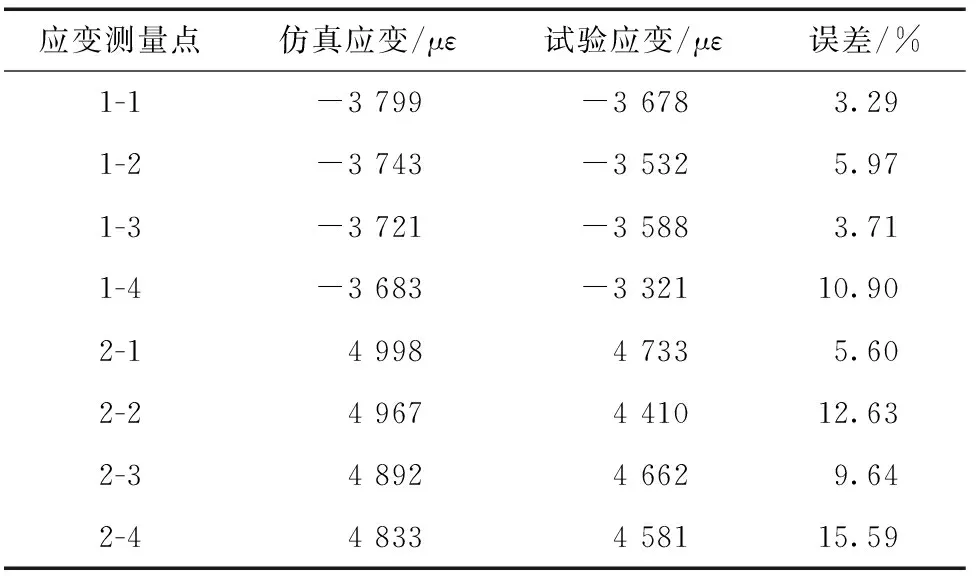
表3 应变数据对比Table 3 Comparison of strain data

机翼扭转角误差超过20%，分析其原因是沙袋加载方式对弦向载荷压心控制不准确所致。

4 结论

基于RX1E-A飞机机翼对考虑翼型弯度的涡格法气动载荷计算方法进行比对研究，并将考虑气动弹性载荷方法在机翼结构铺层优化设计中应用，最后进行结构破坏静力试验，并将试验数据与理论分析结果进行对比，得到以下结论。

(1)通过考虑翼型弯度的面元法可以有效地计算机翼的气动力系数，与CFD计算结果对比升力系数最大误差在8.83%，俯仰力矩系数误差为5.3%。

(2)对于直机翼考虑气动弹性载荷后，载荷相对刚体载荷有所增加，弯矩增加6.23%，扭矩增加3.5%。

(3)基于考虑气动弹性载荷的机翼结构铺层优化设计方法，可以找到整体最优解，相对优化前构型可减重4.74%。

(4)通过静力试验对优化后机翼结构进行验证，仿真结果与试验测量结果有较好的匹配性，计算应变最大误差为15.59%，翼尖位移误差为9.02%。通过沙袋加载方式载荷弦向压心很难控制，因此翼尖扭转角误差较大为24%。