有效开展数学结构化学习——以苏教版三下《认识一个整体的几分之一》的教学为例

施 丽

美国教育家布鲁纳认为：“学习一门学科，就是要掌握这门学科的基本结构。”数学常被称为“结构的科学”，它的学科知识之间有着千丝万缕的关联。数学结构化学习，是指建立在数学知识系统和学生已有认知的基础上，以动态建构为核心，以整体关联为抓手，以思维发展为方向，以数学素养培育为目标追求的学习过程、学习方式和方法。在数学教学中倡导结构化学习，有助于学生将新获取的个别的、无规律的、零散的知识进行分析、筛选、归纳后纳入自己原有的数学知识网络中，最终在头脑中形成更加完善的认知结构。在开展数学结构化学习时，要注意突出整体性、关联性、系统性，站在整体、联系、系统的高度把握和处理教材，引导学生充分把握和感受数学的知识结构，体验数学知识的形成、发展和运用过程。下面，笔者以苏教版三下《认识一个整体的几分之一》一课的教学为例，谈谈如何有效开展数学结构化学习。

一、依据知识结构，让课堂从“线性”走向“网状”

“线性”的课堂以教学内容的逻辑为依据，以主要问题为连接点，以提出问题、分析问题和解决问题为基本操作手段，整个教学过程仿佛连成了一条由一个个具有严格间距的教学环节所构成的直线一般，虽然操作上严密且易把握，但是一旦教师“圈”得过牢，“把”得过多，课堂就易变得亦步亦趋，最终可能导致学习空间的窄化和学生思维的僵化。在“网状”的课堂中，教师以联系的观点组织教材，以发展的手段设计教学过程，引导学生将获取的“线性”知识结构进行整理，重组到自己的知识网络中，让知识元素有机联系。数学结构化学习让课堂从“线性”走向“网状”，要求教师从知识结构入手，立足整体，统揽全局，摆脱课时束缚，把握知识之间的内在关联，促进知识的融合和沟通，让学生知一节联一片。如在导入环节，教师遵循知识的序列化，注重知识网络框架的搭建，以故事切入，复习了三上“认识分数”的内容，并强调分数与份数有关，为接下来的新知学习做铺垫。

师：有一个叫花果山的地方，山上有许多猴子。正逢收获的季节，猴王正在给小猴们分山果呢，瞧！猴王给两只小猴带来了什么呀？（一个桃）

师：两只小猴，一个桃，怎么分？

生：平均分。

师：那在图上可以怎么表示平均分呢？

生：用虚线从中间分开。

师：真好！把1 个桃平均分给2 只小猴，每只小猴能分得这个桃的几分之几呢？

生：每只小猴能分得这个桃的二分之一。

师（指名解释二分之一后）：真厉害！每只小猴分得半个桃，大家想到用分数二分之一来表示，还关注到分母2 表示2 份和分子1 表示1份，也就是说分数与份数有关（板书“份数”）。

二、生成模块结构，让教学从“个别”走向“整体”

按部就班地教学局部知识是一种个别性的教学行为方式，不利于学生获得完整的知识体系，也会使学生学习迁移能力的培养效果大打折扣。数学结构化学习呈现出从个别性走向整体性的趋势。它要求教师聚焦模块教学，大胆优化教学内容，让学生学一块通一类。本节课中，“辨析模块”“探究模块”和“完善模块”这三个教学模块始终围绕“分数与份数直接相关，与数量无关”的主题，展开充分的辨析、自主的探究和实践的完善与总结，让知识的深度得以凸显。

“辨析模块”初识二分之一的知识，受物体个数的影响，学生很容易出错，教师直面普遍问题，给学生提供讨论的空间，引导他们在不断质疑和讨论中关注“整体”。

师：把一盘桃（6 个）平均分给2 只小猴，每只小猴分得这盘桃的几分之几？请在小组内充分讨论后再汇报。

生1：我认为是六分之三，因为一共有6 个桃子，每只小猴分得了3个。

生2：我认为是二分之一，因为是把一盘桃平均分成2份，每只小猴分得了其中的1份。

生3：我认为六分之三和二分之一都可以。

师：我听明白了，认为是六分之三的同学，你们的意思是每只小猴分得3 个，而认为是二分之一的同学，你们的意思是每只小猴分得1份，是吧？看来咱们的分歧就出在份数与个数上。同学们，没关系，在学习道路上遇到新问题时，咱们不妨退到一开始而又不失去重要性的地方去重新思考，也就是分数与何有关联（指着板书“份数”），现在你觉得到底哪个分数更合适呢？

生：二分之一。

师：认为是六分之三的同学还坚持吗？（生摇头）为什么不坚持了？

生：因为黑板上二分之一不是指2 个桃子，而是指平均分成2 份，那六分之三就应该是平均分成6 份，这里是平均分成了2 份，所以是二分之一才对。

“探究模块”深入认识二分之一的知识，教师引导学生自主画一画、分一分，并结合对比各种画法与分法的相同点与不同点，使他们从整体上关注到平均分与桃子的数量没有直接关系，从而加深对二分之一的理解，不断完善认知结构，发展思维能力。

师：这一盘桃，大家会分了，可淘气的猴王又准备了一盘桃，不知道有多少个，仍然平均分给2 只小猴，每只小猴又能分得这盘桃的几分之几呢？在学习单（如下页图1）上画一画、分一分，并根据自己的画法填一填。

生汇报：把4 个桃平均分成2 份，每只小猴分得这盘桃的二分之一；把8 个桃平均分成2份，每只小猴分得这盘桃的二分之一；把3 个桃平均分成2 份，每只小猴分得这盘桃的二分之一……

师：同学们真厉害，想到了这么多种画法，咱们来仔细看看这些画法和分法，有什么相同的地方呢？

生：无论哪种分法，每只小猴都分得这盘桃的二分之一。

师：真爱观察！它们又有什么不同呢？

生：每盘桃个数不同，每份桃个数也不同。

师：这就奇怪了，每盘桃个数不同，每份桃个数也不同，为什么都能用二分之一表示呢？

生：因为都是平均分给2 只小猴，每只小猴分得2份中的1份。

师：真了不起！4个、6个、8个甚至更多桃，我们都看成一盘桃，只要把一盘桃平均分成2份，每份就是这盘桃的二分之一。

“完善模块”认识三分之一的知识，与上述两个模块一起，让学生在环环相扣的活动中完善和提升，让教学逐步走向整体。

师：听到有桃分着吃的消息后，又来了一只小猴。想一想，这时猴王会怎样分这盘桃？如果把一盘桃平均分成3 份，每份是这盘桃的几分之几？

生：三分之一。不管有多少个桃，把一盘桃平均分成几份，每份就是它的几分之一。

三、拓展练习结构，让思维由“单一”走向“多元”

数学结构化学习能促进学生的思维由单一化走向多元化，这一点尤其体现在数学课堂练习上。教师应轻于题海战术，重于题质推敲，探索对比变式性题组练习，让学生练一组长一技。本节课的巩固练习是在教材的基础上进行变式重组的，将“一个物体”和“一个整体”进行直观对比分析，使学生在题组练习中清楚地掌握了分数的内涵，最终理解了“一个整体”的本质，为学生从单一认知到多元思维创造了更加有利的条件。

出示练习题：数一数，比一比，用数表示涂色部分。（逐步出示图2中的各个元素）

追问：相同的苹果，为什么可以用不同的数表示呢？

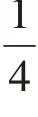
生：因为左边是2个正方体，用2表示；而右边是把8 个正方体看作一个整体，平均分成4份，每份就是它的四分之一。

师：同学们真厉害！对“一个整体”的认识真深刻！

总之，要有效实现数学结构化学习，需要教师在正确解读新课程理念的基础上，多维度地为学生创设条件，让学生在学习中形成良好的认知结构，让数学学习深度发生。