“‘关·联’数学”的教学主张与实施策略

刘丽娟

一节课的呈现不可能是孤立的，既要追问它的知识基础、方法基础，又要考虑其今后的延展。笔者在日常教学中发现，不少教师的教学容易走入两个极端：一是过度瞻前顾后，大量占用本节课的教学时间和内容，导致本节课的教学目标难以达成；二是只着眼于当下，不提供让学生经历知识发生、发展过程的机会，致使学生被动学习。基于此，我们研究团队于2016 年提出“关联数学”的教学主张，并于2017年申报江苏省“十三五”规划立项课题获批。历经两年多的研究，我们的视角从单纯关注文本扩展到关注学情，从分别关注教与学扩展到关注教与学的关系，从关注文本结构扩展到关注师生数学素养的提升，我们的教学主张也转变为“‘关·联’数学”。

一、“‘关·联’数学”的内涵诠释

“关”，作为名词的解释有“事物或时间演进过程中的重要时刻、阶段”，作为动词的解释有“牵连、涉及”。“‘关·联’数学”的“关”可以理解为知识发生过程中的重难点和关键处，以及知识点之间的相互衔接与联系，指向学习内容、知识之间纵向和横向的关系，概念要素之间独立和并存的关系，思想方法之间部分和整体的关系，学科之间内部与外部的关系，等等。“联”，作为动词的解释有“连接、连续；结、结合”。“‘关·联’数学”的“联”可以理解为由此及彼、举一反三，在相关、相似和相通的内容中寻找共同本质，指向学生的思维发展。“‘关·联’数学”从“关”和“联”两个方面展开研究，基于文本的“关”和思维的“联”二者关系的思考，落于教师的“关”和学生的“联”二者关系的设计，它们的关系如下页图1所示。

二、“‘关·联’数学”的理论依据

美国语言哲学家格赖斯说：在关系范畴底下，我只使用一条原则——要有“关联”。加拿大学者西门思提出了连接主义学习理论的六点主张：一是学习是将知识节点或信息源连接在一起的过程；二是保持连接对于持续学习非常重要；三是保持知识的即时性和准确性是一切关联学习的目标；四是寻找知识的能力比现有知识更重要；五是核心能力是发现不同领域、观点和概念之间的联系；六是学习知识存在于多样化观点中。美国心理学家桑代克提出了联结主义学习论，他认为学习要遵循三条重要原则：一是准备律，指学习者在学习开始的预备定势；二是练习律，指一个学会了的反应的重复将增加刺激反应之间的联结；三是效果律，如果一个动作跟随着情境中一个满意的变化，在类似的情境中这个动作重复的可能性将增加，反之则减少。美国数学教师协会2000 年颁布《中小学数学原则与标准》，“数学联系”成为其十条标准之一。这些对关联的理解和定位表达和支持了“‘关·联’数学”的核心思想，即学习源于“关”，指向“联”。

东北师范大学史宁中教授在其主编的《义务教育数学课程标准（2011 年版）解读》一书中多次提到“关联”：教材的编写应考虑学段的关联，以利于学生学习的延续性；教材编写应整体考虑知识之间的关联，不同知识之间、不同课程领域之间都存在实质性联系，教材应着重体现这些联系，而不是忽略它们；各学段数学教材在整体设计时应考虑如何反映课程内容之间存在的实质性联系，这既包括不同领域内容之间的实质性联系（如代数与几何之间、代数与统计概率之间的联系），也包括相同领域内容之间的联系。史宁中教授的观点对“‘关·联’数学”具有很强的指导意义。“‘关·联’数学”教学正是教师基于对文本的整体认识，找准知识的内在实质性联系，引导学生通过想象迁移、比较沟通、拓展创新，在一次次关·联中提升数学素养的活动。

三、“‘关·联’数学”的实施策略

1.找准关点，确立联动目标。

每一节课、每一次活动都有其独特的价值追求，它们既不是单纯对上一节课的重温，也不是盲目对下一节课的越位。只有准确地找到这个关点，才能科学地制定课时目标，从而合理地规划要达成的目标。为了更好地落实国家课程标准的总目标，使之更贴近地方办学特点，凸显学校办学特色；更好地细化年段目标，使之更贴近学生的成长背景，符合每一位学生的认知水平，我们开展了“学习目标能级系列化”研究，具体做法如图2所示。

如教学苏教版三下“两位数乘两位数”单元，要通过每一节课的关点，有效落实课程标准中“能计算两位数乘两位数的乘法”的总目标。第2 课时《两位数乘两位数（不进位）》的教学重点（即关点），是两位数乘两位数（不进位）的笔算，它是多位数乘一位数笔算方法的扩展，是两位数乘两位数（进位）的基础。学生用第二个乘数个位上的数去乘第一个乘数，已经具备了显性基础，但用第二个乘数十位上的数去乘第一个数，只具备隐形基础——乘的方法和顺序与上一步相同，但乘得的结果如何表达（特别是定位问题）是新的内容，需要连接上节课的内容加以理解。正是在这样突破与连接一个个关点的过程中，学生不断建构学习框架、完善自我认知体系。

2.明晰关子，连接新旧认知。

关子比喻事情的关键，它在解决困难或分歧时起决定性作用。数学学习逻辑性很强，一环套一环，无论哪个环节出了问题，学习就会“掉链子”。这个链子，从开始时的线状连接到后来的网状连接，慢慢形成各式各样的立体状连接。要让连接的点更加牢固，教师就要明晰每个关子，并帮助学生理解、内化、掌握和熟练应用它。

如教学《两位数乘两位数（不进位）》一课，要引导学生掌握笔算方法，关键在于两点：一是要掌握乘的顺序，即先用第二个乘数个位上的数去乘第一个乘数，再用第二个乘数十位上的数去乘第一个乘数，最后把两次乘得的结果相加；二是要理解和掌握用第二个乘数十位上的数去乘时得到的数的末位要和第二个乘数的十位对齐，这个关子既需要运用前面的旧知来突破，也直接影响着下一节课《两位数乘两位数的进位乘法》的学习。在教学中，以前学过的两、三位数乘一位数的笔算方法有助于学生进行方法迁移，完成第一次乘积过程。上一课时的学习内容有助于学生预估新知24×12 的计算结果，同时有助于学生完成第二次乘积——10 乘两位数和整十数乘整十数。最关键的是，还能帮助学生理解“为什么竖式计算时用第二个乘数十位上的数去乘第一个乘数，乘得的末位应写在十位上”。明晰关子，既是对教师解读文本、设计教法和指导学法的要求，也是对学生温故知新、自主建构和综合运用的挑战。

3.辨析关系，联系数学思想。

事物的关联极其复杂，在内容和形式上多种多样，不同的关联对事物的存在和发展所起的作用不同。教师在数学教学中要抓住这些联系，培养学生主动联想的学习习惯和关联思考的思维方式，从而使他们对数学学习内容形成整体的认知。数学表达也不是千篇一律的，多维比较、辨析这些表达的异同，从关系的角度审视它们，渗透数学思想，能促进学生的学习由浅层转向深层。

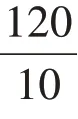
4.融通关节，促进联想生成。

华东师范大学叶澜教授认为，现代学校教育系统的总体结构在形式上呈现为四层阶梯状，其中第四层次为教与学的配合以及教向学的转化。该层次的任务是把教师提出的对学生的要求内化为学生的自觉要求，把教育内容内化为学生个体的身心发展。这就要求教师在对教学内容结构化重组时，要注重整体性、长效性和发展性，要满足学生在学习中自主迁移、前思后虑、触类旁通的需要。

如教学“两位数乘两位数”单元，可以先让学生想一想：两位数乘两位数有哪些类型？学生经历过数的类型和两位数乘一位数类型的整体认知过程，因而很容易就能得出两位数乘两位数可以分成整十数乘整十数、两位数乘整十数和两位数乘两位数（这里的两位数是指非整十数的两位数），而两位数乘两位数又可以分为不进位和进位两种。学生凭借学习经验，可能做到的迁移有：学习的先后顺序是从易到难——先学和整十数相乘的，再学不进位的，最后学进位乘；整十数的关键作用是学到不进位的时，能想到把非整十数看成和它最接近的整十数来乘或者拆成和整十数相关的数来乘……学生今天的迁移源于以往的经验积累，以及教师对文本的智慧处理。教学新知时，教师应注重引导学生调动自己内在的认知需求和经验，在感知、经历、理解和内化的过程中建构自己新的认知框架。

总之，“‘关·联’数学”就是这样，基于教和学的双边共生，通过四个环节的层层推进，实现师生的双向共学和素养提升。