对一道中考试题的再探究

孙静

1 原题呈现

武汉市2019年中考数学第16题：

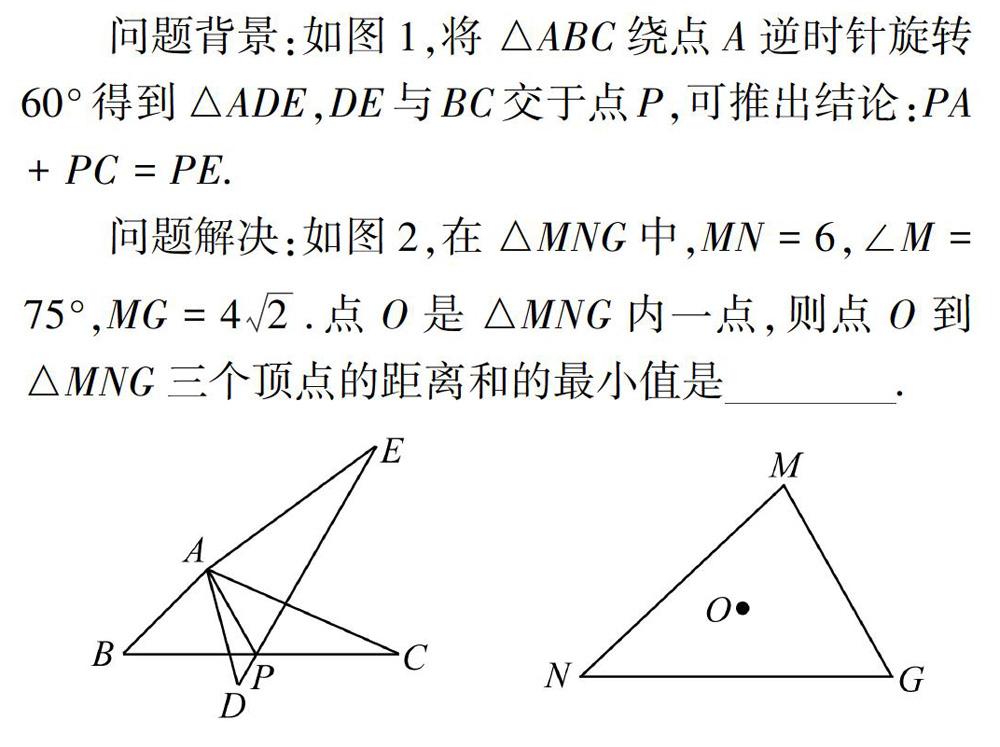
问题背景：如图l，将△ABC绕点A逆时针旋转60°得到△ADE，DE与BC交于点P，可推出结论：PA+PC=PE。

辅导中，许多学生面对此题茫然无措，不知从何处下手。我们引导学生重点思考以下两个问题：①题目中的问题背景与后续问题之间有怎样的内在联系？②前后图形之间是否有相同或相似之处？

2 思路分析

2.1 从图形人手，寻找二者之间的相同或相似之处

经过前述铺垫，部分学生很快找到了突破口：图1中隐含着一个△ADC，其中的点P很可能就是图2中要寻找的点O的特殊位置。该位置能使点O到△MNG三个顶点的距离之和最小。

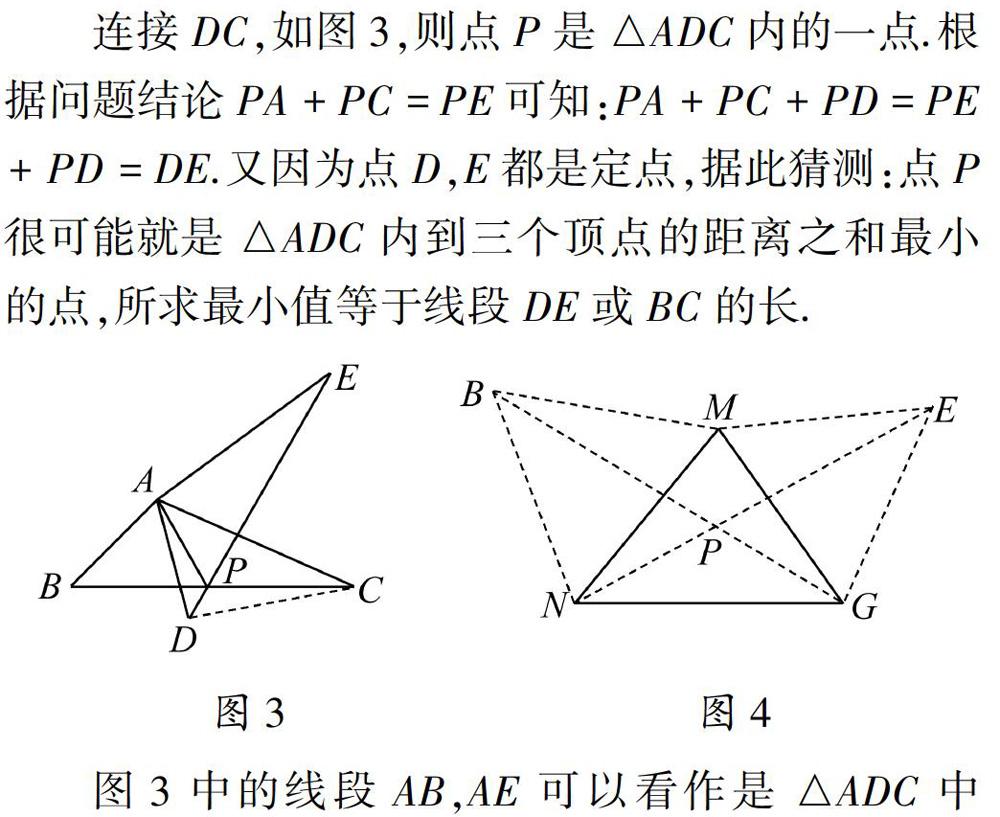
连接DC，如图3，则点P是△ADC内的一点。根据问题结论PA+PC=PE可知：PA+PC+PD=PE+PD=DE。又因为点D，E都是定点，据此猜测：点P很可能就是△ADC内到三个顶点的距离之和最小的点，所求最小值等于线段DE或BC的长。图3中的线段AB，AE可以看作是△ADC中∠DAC的两边分别以点A为中心向三角形外部旋转60°得到的。仿照图3，构造图4，则BG或NE的长很可能就是题目中要寻找的最小值。

2.2 从文字人手，寻找二者之间的内在联系

3 继续探究

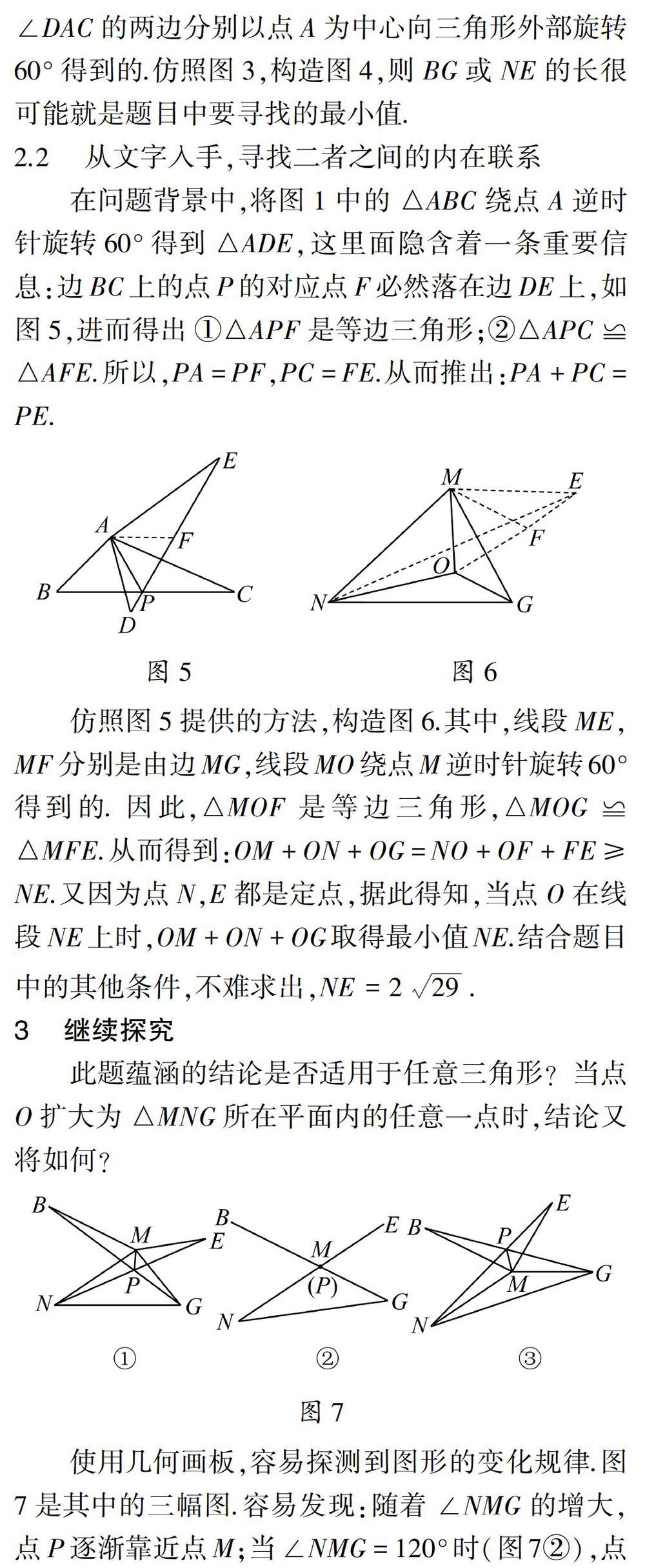
此题蕴涵的结论是否适用于任意三角形？当点O扩大为△MNG所在平面内的任意一点时，结论又将如何？

使用幾何画板，容易探测到图形的变化规律。图7是其中的三幅图。容易发现：随着∠NMG的增大，点P逐渐靠近点M;当∠NMG=120°时（图7②），点P与点M重合，此时NE=MN+MG：当120°<∠NMG<180°时（图7③），点P移出△MNG。此时，PG=PM+PE。PM>0.所以。PM+PN+PG=NE+2PM>NE，上述结论不再成立。

4 归纳结论

5 教学思考

本例教学启示我们，为了培养学生的问题探究能力，应重视以下几点：

5.1 要重视培养学生挖掘隐性条件的能力

许多试题除了明白表达的显性条件外，往往还含有深藏于字面之下图形之中含而不露的隐性条件。如何挖掘出这些隐性条件，往往成为解决这类问题的关键。为此，我们不仅要重视培养学生掌握扎实的基础知识。还要重视培养学生学以致用的应用意识和丰富的想象能力、联想能力、猜想能力、推理能力和几何直观能力等。

5.2 要让学生经历探究的过程

《义务教育数学课程标准（2011年版）》中提到：课程内容要符合学生的认知规律。它不仅包括数学的结果。也包括数学结果的形成过程和蕴涵的数学思想方法。在辅导学生处理本题时。我们采用了引导而不是简单传授的方法，让学生经历结论的获得过程，教师尽量“不愤不启不悱不发”，引领学生“绝知此事要躬行”。

5.3 要重视培养学生深入思考某一问题的能力

深入思考某一问题。才能彻底“消灭”这一问题。这种经历经久难忘，并会最终形成一种强大的能力，“辐射四方”。看似浪费时间，其实节省时间。它为后续学习扫清了障碍，化负担为动力，使学生轻松上阵。蟾蠍行路，越积越重：夏季流冰，渐行渐轻。

5.4 要重视现代信息技术手段在教学中的应用

本例正是利用了几何画板提供的直观和便利，动态地展现了数据随图形变化的过程，使学生能够清楚地看见事件发展的全貌，从而激发探究的欲望，这是传统教学手段很难做到的。