中小学生计算思维能力影响因素分析
赵明 王小红 杨冬 朱道鑫 罗建坤
摘要:计算思维能力被认为是未来创新型人才必备的基本技能之一,世界各国的教育工作者和研究者开展了大量促进和培养学生计算思维能力的实证研究。然而,却鲜有研究者对计算思维能力的影响因素进行探究。文章在已有的促进学生计算思维能力发展的研究基础上,对影响学生计算思维能力的因素进行了梳理。采用问卷调查法和分层多阶段整体抽样方法在成都市选取了302名中小学生作为研究对象,通过对回收数据的分析,构建和验证了影响因素结构方程模型。研究结果发现,学生的科学态度、数学态度和思维风格对计算思维能力有显著的正向影响,信息技术态度对计算思维能力有显著的负向影响,性别、学段、先前经验和数学成绩对学生的计算思维能力没有显著性影响。
关键词:计算思维;影响因素;创客教育
中图分类号:G622 文献标志码:A 文章编号:1673-8454(2020)06-0001-06
计算思维能力如同阅读、写作和数学等基本技能一样,成为21世纪创新型人才必备的基本技能之一。为了在日益增长的全球经济中保持竞争力,世界各国的教育改革皆提出要加强对学生计算思维能力的培养。在此背景下,国内外学者主要对计算思维定义及如何促进学生计算思维能力的发展进行了大量相关研究,鲜有研究者关注K-12教育中学生的相关因素对计算思维能力的影响。基于此,本研究在借鉴已有促进学生计算思维能力发展研究的基础上,对影响学生计算思维能力的因素进行了梳理,然后采用定量研究的方法以探索计算思维能力与各因素之间的关系,进而探寻培养学生计算思维能力的有效路径,为我国更好地开展培养学生计算思维能力的教育提供借鉴与建议。
一、研究假设的提出
1.性别和学段
Hsu等人[1]认为编程语言是培养学生计算思维能力最简单、最合适的方法。已有的研究表明,编程自我效能感与能力的高低与计算思维能力之间存在着显著性的关系,并且性别不同对编程活动、机器人等也持有不同的态度。Askar和Davenport[2]探讨了性别与编程自我效能感、编程能力的关系,研究表明男生在编程自我效能感及编程能力方面均高于女生。Kiss[3]认为与女生相比,男生更有可能发展编程技能,并且对编程更感兴趣。Román-González等人[4]通过对5-12年级的学生进行干预,研究结果表明学生的计算思维能力在性别方面存在差异性,男生比女生更占优势。然而,Werner等人[5]的研究结果却表明学生的计算思维能力与性别没有显著性关系。类似的结论我们在Atmatzidou等人[6]的研究中也能看到,他们认为计算思维能力虽然不因年龄和性别而异,但是女生则需要付出更多的努力和时间才能达到与男生相同的计算思维能力水平。通过已有的研究我们可以发现,计算思维能力与性别差异是否存在影响关系尚未有统一的研究结论,因此本研究就性别差异对学生计算思维能力的影响关系提出以下假设:
H1:学生的性别对计算思维能力有显著影响。
在探讨学段与计算思维能力之间关系的研究方面,Basogain等人[7]将计算思维定义为与认知发展相关的技能,并认为学生的学段与计算思维能力之间可能存在相應的关系。在Román-González等人[4]的研究中不仅发现学生的学段与计算思维能力之间存在正相关关系,还认为学生的认知发展水平和成熟度水平是影响学生计算思维能力发展的重要因素。关于学生学段与计算思维能力之间关系的研究还相对较为缺乏,然而明确学生的学段对计算思维能力的影响程度却是一个不容忽视的问题。基于此,本研究就学生的学段对学生计算思维能力的影响关系提出以下假设:
H2:学生的学段对计算思维能力有显著影响。
2.学生的先前经验
计算机科学被公认为是培养学生计算思维能力的一个重要领域。编程教育有助于培养学生的计算思维能力,已有研究表明编程包括展示设计的产品和计算思维能力。此外,美国国际教育技术协会(ISTE)和美国国家科学研究委员会(NRC)认为学生即使不使用技术工具进行创造性实践,他们也能展示计算思维能力。换而言之,学生与技术的互动是反映学生计算思维能力的一个重要方面。基于此,我们认为学生的先前经验(使用计算机方面的经验)可能对其计算思维能力产生影响,并提出以下假设:
H3:学生的先前经验对计算思维能力有显著影响。
3.学生对数学、信息技术和科学课程的态度和数学成绩
计算思维这一概念不仅与计算机科学相关,而且它和数学、科学也有着紧密的关系。换而言之,虽然计算思维一直在使用计算机科学的一些基本概念,但它在发展数学和科学常用的技能(比如问题解决能力、算法思维、抽象等)方面仍具有重要的作用。Perkins等人[8]认为学生在学习数学、科学、计算机科学和编程等领域中相似的概念和技能时,在数学、科学、计算机科学等学科有着相同的根源。Hambrusch等人[9]认为计算思维的子技能(如算法思维、批判性思维等)是学习数学和科学的有效工具。学生对数学和科学的态度是否会对计算思维能力有影响的研究还较为缺乏。已有研究表明学生的态度与课程的成功有着显著性关系,因此学生对数学的态度是影响数学成绩的重要因素之一。基于此,本研究将探讨计算思维能力与学生对数学、科学的态度及数学成绩之间的关系,并提出以下假设:
H4:学生对数学的态度对计算思维能力有显著影响。
H5:学生对科学的态度对计算思维能力有显著影响。
H6:学生的数学成绩对计算思维能力有显著影响。
Korkmaz等人[10]认为计算思维的概念和应用以计算机和计算机科学的基本概念为基础。计算思维包括与计算机科学相关的基于认知和应用的知识结构,比如问题的表示和解决、抽象等。此外,Sengupta等人[11]认为计算思维使用着和计算机科学相关的基本概念与主题。因此,Kafai和Burke [12]认为在K-12阶段应该设计能够激发学生对计算机科学兴趣的相关主题来培养计算思维能力。
从上述观点来看,为学习计算思维技能而创建的应用程序必须以和计算机科学交织在一起的方式进行设计。K-12教育中的编程与学习计算机系统的工作系统之间有着密切关系,并且与计算机系统相关的主题可以构成培养计算思维的有效工具。在教学过程中学生所取得的成就是通过超越知识、技能的态度和价值观来实现的,由于我国K-12阶段的学生在学校教育中接触计算机科学的主要途径为信息技术课程,因此本研究提出以下假设:
H7:学生对信息技术的态度对计算思维能力有显著影响。
4.学生的思维风格
思维风格是指个体在寻找解决方案时倾向于使用的与技能、知识和能力相关的表现方式。学生需要掌握一些思维技能才能适应知识爆发式增长的时代,才能成为21世纪的创新型人才。从计算思维的定义和应用来看,计算思维包括问题解决、算法思维、分析思维等能力,它是学生必备的思维技能之一。Barr等人[13]认为计算思维与批判性思维、数学思维和算法思维的区别在于:计算思维是一种新的强大的组合,它通过使用不同的思维技能来解决问题。由此来看,不同的思维技能能够与计算思维结合在一起形成一个思维系统。在这个思维系统中,学习者的思维风格将是获得计算思维能力的重要组成部分。因此,在学生思维风格对计算思维能力的影响关系这方面,本研究提出以下假设:
H8:学生的思维风格对计算思维能力有着显著影响。
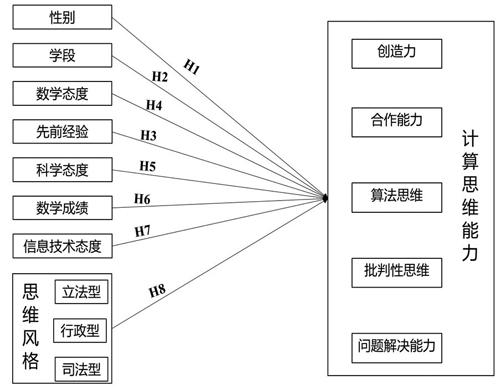
基于上述文献综述确定的8个假设,本研究确定了计算思维能力的8个影响因素,分别为性别、学段、先前经验、数学态度、科学态度、数学成绩、信息技术态度、思维风格,并构建了如图1所示的假设模型。
二、调查与数据收集
1.研究对象
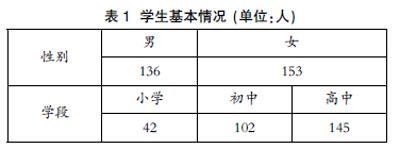
本研究采用分层多阶段整体抽样方法,在成都市选取了302名中小学生为研究对象,其中小学生42人(占14%),初中生107人(占35%),高中生153人(占51%);女生155人(占51%),男生147人(49%)。参与此次调查的学生皆为自愿参与,我们以问卷星的形式发布本研究中所使用到的相关量表,并由信息技术课教师在课堂上引导学生填写问卷,问卷共回收302份,回收率为100%,经剔除无效问卷后,有效问卷共289份(占96%),具体如表1所示。
2.研究工具
本研究使用的问卷由三部分构成,包括个人信息、思维风格和计算思维能力。个人信息部分由研究者根据国内外学者已有研究,与领域专家共同讨论后编制,该问卷共包含13个题目,主要收集参与者的先前经验、数学成绩、数学态度和科学态度信息。问卷项目因问题而异,一般具有李克特量表性质。计算思维能力量表由Korkmaz等人[10]编制而成,该量表原本的使用对象为在校大学生,包含创造力、合作能力、算法思维、批判性思维和问题解决能力5个维度,共29个题目。后经Korkmaz等人的修改并将题目减少至22个,使之适用于中小学生,修改后的量表依旧包括原有的5个维度。
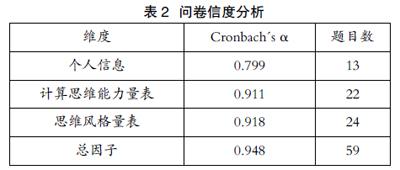
本研究将计算思维能力量表进行了本土化翻译并适度修改,利用SPSS 20.0进行了信效度检验。思维风格量表由Sternberg 等人[14]编制而成,该量表旨在揭示主导的思维风格,包括5个维度下的13种思维风格,共104个题目。本研究选用立法、行政和司法三个因素构成的24个题目,进行本土化翻译和适度修改后又进行了信效度检验。最终,本研究所使用的总体问卷共59个题目,Cronbach's α系数为0.948。总问卷题目及各部分问卷题目均有较高的内部一致性,结果如表2所示。
本研究采用的分析方法为探索性因子分析,在总体问卷中共抽取12个因子,经分析后KMO值为0.906,Bartlett的球形度检验显著(p=0.000)。数据表明,总体问卷的题目之间存在着共同因素,效度良好,并且能够解释各个变量之间的关系,适合用来进行因子分析。问卷效度检验结果如图2所示。
三、数据分析结果
1.描述性统计
此次研究对象的中小学阶段数学成绩为百分制,而初中和高中阶段的数学成绩为150分制。因此我们在SPSS 20.0中进行数据分析前,需要将百分制的成绩转换为150分制成绩(转换公式:当前百分制成績×1.5)。经分析,数据样本的各变量二点平均值、标准差和相关系数如图3所示。从数据分析结果可以发现,被测学生的计算思维能力(M=3.569,SD=0.548)为较好的水平,说明学生具有一定的计算思维基础;先前经验(M=3.714,SD=0.851),说明被调查学生在使用计算机方面具有丰富的经验;数学态度(M=3.765,SD=0.883),说明被调查的学生对数学具有较高的态度;科学态度(M=3.937,SD=0.734),说明被调查的学生对科学具有较高的态度;信息技术态度(M=3.326,SD=0.692),说明被调查的学生对信息技术具有较高的态度。
我们从各个变量因素之间的相关性进行分析后发现,除了数学成绩和学段外,性别、先前经验、数学态度、科学态度、信息技术态度、立法型思维风格、行政型思维风格和司法型思维风格的显著性概率值都为p<0.01,其中,行政型思维风格与计算思维能力存在强相关(相关系数r<0.8),其余因素与计算思维能力存在中低度相关(相关系数r<0.6)。性别和学段与各变量之间相关程度偏低,性别与数学态度、信息技术态度、司法型思维风格、计算思维显著性概率都为p<0.01,说明学生的性别与学生数学态度、信息技术态度、司法型思维风格、计算思维线性相关性很强。
2.回归分析
为了对本研究提出的假设进行验证,我们对各变量进行了回归分析,以了解变量间相关性的因果关系。
(1)计算思维能力与影响因素的回归分析
我们将学生的计算思维能力作为因变量,以其影响因素中的性别、学段、数学成绩、先前经验、数学态度、科学态度、信息技术态度、思维风格8个变量作为自变量。其中,我们将思维风格自变量具体划分为立法型、行政型和司法型3个维度,然后进行回归分析并构建了模型,数据分析结果如表3所示。
由表3可知,学生的计算思维能力与其影响因素的多元相关系数R为0.737,判定系数R2=0.542,调整后R2=0.526,上述数据表明8个影响因素对因变量有73.7%的信息解释度,所建立的回归模型整体解释变异量达到显著水平(F=32.962,p<0.001)。影響学生计算思维能力的因素从小到大依次为:学段、数学成绩、先前经验、性别、信息技术态度、立法型思维风格、司法型思维风格、科学态度、数学态度、行政型思维风格。因此,我们可以得到计算思维能力的回归方程为:
Y计算思维能力=常量+0.006×学段+0.016×数学成绩+0.037×先前经验-0.058×性别-0.073×信息技术态度+0.183×科学态度+0.219×数学态度+0.126×立法型思维风格+0.309×行政型思维风格+0.175×司法型思维风格
(2)计算思维能力与各个影响因素的回归分析
周以真(Jeannette M.Wing)首次提出计算思维是每个人必备的基本技能之一,之后“计算思维”一词在全世界范围内开始变得流行起来。目前学术界关于计算思维的定义有很多,但却没有达成统一共识。在本研究中,我们采用被高度认可的美国国际教育技术协会(ISTE)于2015年给出的计算思维定义:计算思维由创造力、算法思维、批判性思维、问题解决能力和合作能力5个部分构成。因此,我们将计算思维能力的创造力、合作能力、算法思维、批判性思维及问题解决能力5个维度作为因变量,将8个影响因素作为自变量依次进行回归分析,可以发现:
①影响创造力的回归分析
以计算思维能力中的创造力维度为因变量,从分析结果可以发现创造力与影响因素的多元相关系数R为0.686,判定系数R2为0.471,调整后R2为0.452,表明8个影响因素对创造力维度有68.6%的信息解释度。其中,科学态度、信息技术态度、思维风格(立法型、行政型和司法型)对创造力具有显著影响。性别、学段、数学成绩、先前经验和数学态度等5个影响因素对学生的创造力没有显著性影响。
②影响合作能力的回归分析
我们将计算思维能力中的合作能力这一维度作为因变量,发现合作能力与影响因素的多元相关系数R为0.594,判定系数R2为0.353,调整后R2为0.330,表明8个影响因素对合作能力维度有59.4%的信息解释度。其中,科学态度、行政型思维风格和司法型思维风格对合作能力具有显著性影响,其余影响因素对学生的合作能力没有显著性影响。
③影响算法思维的回归分析
当我们以计算思维能力中的算法思维这一维度作为因变量时,发现算法思维与影响因素的多元相关系数R为0.622,判定系数R2为0.387,调整后R2为0.365,表明8个影响因素对算法思维维度有62.2%的信息解释度。其中,数学态度、行政型思维风格和司法型思维风格3个影响因素对算法思维具有显著性影响,其余影响因素对学生的算法思维没有显著性影响。
④影响批判性思维的回归分析
以计算思维能力中的批判性思维这一维度作为因变量进行分析时发现,批判性思维与影响因素的多元相关系数R为0.709,判定系数R2为0.503,调整后R2为0.485,表明8个影响因素对批判性思维维度有70.9%的信息解释度。影响因素中的数学态度、科学态度、思维风格(立法型、行政型和司法型)对学生的批判性思维具有显著性影响,其余影响因素对学生的批判性思维没有显著性影响。
⑤影响问题解决能力的回归分析
以计算思维能力中的问题解决能力这一维度作为因变量进行分析发现,问题解决能力与影响因素的多元相关系数R为0.363,判定系数R2为0.132,调整后R2为0.101,表明8个影响因素对问题解决能力维度有36.3%的信息解释度。影响因素中仅行政型思维风格这一自变量对学生的问题解决能力具有显著性影响。
3.模型分析
通过在SPSS 20.0中分析得到的路径模型(见图4),我们可以发现:①在计算思维能力的创造力这一维度,学生的科学态度和思维风格(立法型、行政型、司法型)对其创造力具有显著的正向影响。学生的信息技术态度对创造力具有显著的负向影响,说明学生对信息技术的态度越高,则创造力越低。现阶段,我国K-12教育阶段中学校及科任教师对信息技术课的重视度不够高,在实际教学中放任学生自由探索,这可能会让学生在潜意识中认为信息技术课是“玩耍课”,导致学生对信息技术课程非常感兴趣,然而在知识与技能方面的收获却非常匮乏。②在计算思维能力的合作能力这一维度,科学态度、行政型思维风格和司法型思维风格这3个影响因素对合作能力具有显著的正向影响。③在计算思维能力的算法思维这一维度,数学态度、行政型思维风格和司法型思维风格对学生的算法思维具有显著的正向影响。其中,学生的算法思维受到数学态度的影响较大,达到0.389。④在计算思维能力的批判性思维这一维度,数学态度、科学态度和思维风格(立法型、行政型和司法型)对学生的批判性思维具有显著的正向影响。⑤在计算思维的问题解决能力这一维度,行政型思维风格对学生的问题解决能力具有显著的正向影响。
综上所述,学生的科学态度、数学态度、信息技术态度和思维风格对计算思维能力有显著影响。进一步分析发现,学生计算思维能力的影响因素主要有以下几方面表现:①科学态度对学生的批判性思维、创造力和合作能力具有显著的正向影响,在培养学生批判性思维、创造力及合作能力方面可通过提高学生科学态度的教学活动来实现。②数学态度对学生的算法思维和批判性思维具有显著的正向影响,这一发现也被Blikstein和Wilensky[15]的研究结论所支持:算法思维是学习数学概念的有效工具,算法思维与数学态度两者相辅相成。③思维风格对学生的问题解决能力、批判性思维、算法思维、合作能力和创造力具有显著的正向影响。换而言之,思维风格对学生计算思维能力具有显著的正向影响。这说明如果在日常的机器人、编程等教学活动中注重对学生思维方式的引导,那么就能更有效地培养学生的计算思维能力。该发现与Cohen[16]的研究结论一致:学习思维风格可以提高学生的创造性学习技能,提高学生解决问题和抽象等技能。④信息技术态度对学生的创造力具有显著的负面影响。Kafai和Burke[12]认为在培养学生的计算思维能力时,可以通过提高学生对信息技术的态度来设计产品实现。然而,本研究的研究结论却表明学生对信息技术的态度越高,那么学生在计算思维能力的创造力这一维度就越低。究竟学生对信息技术的态度能否对学生的创造力或计算思维能力产生影响以及产生什么样的影响,还需要后续进行进一步的深入探究。
此外,性别、学段、先前经验和数学成绩对学生的计算思维能力没有显著性影响。关于性别是否会对学生的计算思维能力有影响这一话题,已有学者进行过相关的研究,但尚未有统一的结论。本研究在性别与学生计算思维能力关系的研究结论与Román-González等人对5-12年级学生进行干预后的研究结果相悖,但却被Werner和Atmatzidou等人的研究结论所支持。然而,Prottsman[17]在其论文中却认为女性在计算机科学和获得计算思维技能方面更有天赋。目前,就性別能否对学生的计算思维能力产生影响,尚未有统一的研究结论,还需进一步研究。就学生的学段和先前经验对计算思维能力的影响关系来说,Durak和Saritepeci[18]认为学段对学生的计算思维能力具有负向的影响,然而在本研究中却发现学段这一因素并不会对学生的计算思维能力产生影响。在Kalelio lu[19]的研究中发现数学成绩能够对学生的计算思维能力产生影响,然而本研究却发现数学成绩与计算思维能力并无关系。
四、总结与展望
在未来培养学生计算思维能力的研究中,本研究建议在教学方法上注重对学生思维进行引导,而不是填鸭式的教学;在教学活动的设计方面,可以根据学生的思维方式设计针对计算思维的活动,提供更简单、更持久的计算思维学习。此外,在日后的教学中可考虑将编程与数学结合,以此提升学生的数学态度与计算思维能力。换而言之,提升学生的数学态度是培养学生算法思维的有效途径之一。因此,编程与学科结合进行教学在未来具有很大的研究空间,值得深入探索。
参考文献:
[1]Hsu T C, Chang S C, Hung Y T. How to learn and how to teach computational thinking: Suggestions based on a review of the literature[J].Computers & Education,2018,126: 296-310.
[2]Askar P , Davenport D . An Investigation of Factors Related to Self-Efficacy for Java Programming Among Engineering Students[J].Online Submission,2009,8(1):26-32.
[3]Kiss G. A comparison of informatics skills by genders of Hungarian grammar school students[A]. In: 2010 7th International Conference on Ubiquitous Intelligence & Computing and 7th International Conference on Autonomic & Trusted Computing[C].Xian,China: IEEE,2010,2:17-27.
[4]Román-González M, Pérez-González J C, Jiménez-Fernández C. Which cognitive abilities underlie computational thinking?Criterion validity of the Computational Thinking Test[J]. Computers in Human Behavior,2017,72:678-691.
[5]Werner L, Denner J, Campe S, et al. The fairy performance assessment: measuring computational thinking in middle school[A]. In: SIGCSE. Proceedings of the 43rd ACM technical symposium on Computer Science Education [C]. New York,NY,USA:ACM,2012:215-220.
[6]Atmatzidou S, Demetriadis S. Advancing students computational thinking skills through educational robotics: A study on age and gender relevant differences[J]. Robotics and Autonomous Systems,2016,75:661-670.
[7]Basogain X, Olabe M A, Olabe J C, et al. Mathematics education through programming languages[A]. In: 21st Annual World Congress on Learning Disabilities [C]. Ovieda, Spain: Learning Disabilities WOLDWIDE,2012:553-559.
[8]Perkins D N, Simmons R. Patterns of misunderstanding: An integrative model for science, math, and programming[J]. Review of Educational Research,1988,58(3): 303-326.
[9]Hambrusch S, Hoffmann C, Korb J T, et al. A multidisciplinary approach towards computational thinking for science majors[J]. ACM SIGCSE Bulletin,2009,41(1):183-187.
[10]Korkmaz ?魻, ?覶akir R, ?魻zden M Y. A validity and reliability study of the Computational Thinking Scales(CTS)[J].Computers in Human Behavior,2017,72:558-569.
[11]Sengupta P, Kinnebrew J S, Basu S, et al. Integrating computational thinking with K-12 science education using agent-based computation: A theoretical framework[J]. Education and Information Technologies,2013,18(2):351-380.
[12]Kafai Y B, Burke Q. The social turn in K-12 programming: moving from computational thinking to computational participation[A]. In: SIGCSE. Proceeding of the 44th ACM technical symposium on Computer science education [C]. New York, NY, USA:ACM, 2013: 603-608.
[13]Barr D, Harrison J, Conery L. Computational thinking: A digital age skill for everyone[J]. Learning & Leading with Technology, 2011, 38(6): 20-23.
[14]Sternberg R J, Grigorenko E L. Are cognitive styles still in style?[J].American psychologist, 1997, 52(7): 700-712.
[15]Blikstein P, Wilensky U. An atom is known by the company it keeps: A constructionist learning environment for materials science using agent-based modeling[J]. International Journal of Computers for Mathematical Learning, 2009,14(2): 81-119.
[16]Cohen A D. Strategies in learning and using a second language[M].2nd Edition. London: Routledge, 2014: 221-225.
[17]Prottsman C L L. Computational thinking and women in computer science[D]. Eugene: University of Oregon, 2011.
[18]Durak H Y, Saritepeci M. Analysis of the relation between computational thinking skills and various variables with the structural equation model[J].Computers & Education,2018,116:191-202.
[19]Kalelio luF. A new way of teaching programming skills to K-12 students: Code. org[J]. Computers in Human Behavior,2015,52:200-210.
(編辑:李晓萍)

