基于GF(28)域上的机密文件分解分存与恢复
刘海峰, 熊 梦, 梁星亮
(陕西科技大学 文理学院, 陕西 西安 710021)
0 引言
随着计算机和网络通信的广泛应用,人们使用电子方式来存储重要机密信息的做法越来越普遍.近年来,网络环境自身也存在着一定的安全隐患,可能会导致重要的信息和秘密数据丢失、以及被不法分子恶意篡改利用等问题.国家还是公司对于上述情况都是不希望看见的,然而目前主要还是通过对数据进行加密、存储等技术方法来实现数据的三大性能,即可用性、可靠性和安全性能[1,2].因此在网络通信中如何安全存放重要的数据,这是所有信息系统都必须关注的关键问题.把重要数据分组存放于不同点,等实际需要时再从部分存放点取出合成是一种非常好的数据保存方式[3].也可以通过密码学的技术手段实现数据安全存储与安全计算[4],但在传统的密码体制中,加密后一旦用户密钥丢失或者损坏,很可能会导致数据泄露或者无法解密,但秘密共享方案就有效的解决了这个问题.
秘密共享是现代密码学的一个重要方向,也是信息安全的一个重要分支,在政治、军事等领域运用十分广泛,其主要的思想就是把一个重要的数据分成不同的份额并由不同的人管理.能够分散安全风险,容忍入侵,不仅可以对隐私数据进行保护,也可以对解密密钥进行保护,防止攻击者对数据窃取、破坏,为密钥管理提供有效的管理.
文献[5]介绍了Shamir于1979年提出的基于一元Lagrange插值的秘密共享方案.其基本思想是通过构建的秘密多项式将共享秘密S分成n份子秘密分发给不同的参与者,当且仅当多于门限数量t个参与者合作才能重构共享的秘密.文献[6]实现了一个基于Lagrange插值多项式的门限方案,包括秘密分割和秘密恢复两方面.文献[7]在Shamir秘密共享方案的基础上讨论此种情形下秘密共享问题,通过引入影子秘密的线性组合——拉格朗日因子来恢复秘密,并进一步将其扩展为一个多秘密共享方案.文献[8]基于单向散列链的特性,提出了一种新型可更新的秘密共享方案.使用单向散列链构造更新多项式,避免了生成随机多项式带来的计算开销.文献[9]针对传统基于插值多项式的秘密分享方案,提出一种结合数据分块方法以及仅需要在GF(2)上的异或运算的秘密分享方案.
然而传统的Shamir方法运算都是在GF(p)上的多项式运算,计算代价过大,当需要分享较大的秘密(如大规模数据)时非常困难,并且效率非常低[10].与此同时,有限域GF(p)中p是素数,但计算机信息系统常采用8个二进制位构成ASCII码或者16个二进制位构成Unicode码,8和16都不是素数,因此在数学上使用GF(2n)域[11]作码字的演算更为合适.
针对上述问题提出一种基于有限域GF(28),利用(t,n)门限对机密文件进行分组拆分、分存和恢复的算法,更适合计算机系统的二进制运算体系,具有很高的运算效率,性能能够得到很大的提升,同时GF(28)域上的运算较为复杂,使得被破解难度增加.
1 有限域GF(28)概述
1.1 有限域GF(28)多项式运算
GF(2n)域中的元素可以表示为式(1)所示:
f(x)=a1xn-1+a2xn-2+…+an-1x+an=
(1)
也可以由它的n个二进制系数(a1,a2,…,an)唯一表示.因此GF(28)域中的每一个元素都可以表示成为一个7次多项式,多项式的系数只能是0或者1.以7次多项式为元素,选用8次不可约多项式m(x)=x8+x4+x3+x+1作为模多项式[11].
有限域GF(28)上的多项式运算[12]定义如下,用⊕表示多项式的加法,用⊗表示多项式的乘法:即对
∀a(x),b(x),c(x)∈GF(28)记a(x)=
其中ai,bi,ci∈{0,1}.有限域GF(28)上相关运算如下:
b(x)⊕a(x))
(2)(a(x)⊕b(x))⊕c(x)=a(x)⊕(b(x)⊕
c(x))
(3)-a(x)=a(x)
(4)a(x)⊕0=a(x)
2)xi+j) modm(x)
(6)a(x)-1:当且仅当a(x)⊗a(x)-1=1 mod
m(x)(a(x)≠0)
(7)a(x)⊗1=a(x)
(8)(a(x)⊗b(x))⊗c(x) modm(x)=
a(x)⊗(b(x)⊗c(x)) modm(x)
(9)(a(x)⊕b(x))⊗c(x) modm(x)=
(a(x)⊗c(x))⊕(b(x)⊗c(x))
modm(x)
(10)c(x)⊗(a(x)⊕b(x)) modm(x)=
(c(x)⊗a(x))⊕(c(x)⊗b(x))
modm(x)
1.2 有限域GF(28)乘法逆元
早在电子计算机时代之前最有名的一个算法就是Euclid算法,现在Euclid算法和扩展Euclid算法在数据加密领域被广泛应用.Euclid算法可以用来求两个多项式的最大公因式,扩展Euclid算法则可以用来求一个多项式的乘法逆元.
如果多项式b(x)的次数小于a(x)的次数且gcd[a(x),b(x)]=1,那么该算法能求出b(x)以a(x)为模的乘法逆元.给定两个多项式a(x)和b(x),其中a(x)的次数大于b(x)的次数,解方程:a(x)w(x)+b(x)w(x)=d(x).获得v(x),w(x),以及d(x),其中d(x)=gcd[a(x),b(x)].如果d(x)=1,则w(x)是b(x)模a(x)的乘法逆元.
2 传统的shamir的(t,n)门限方案
2.1 (t,n)门限中子秘密分发
Shamir的秘密分享方案是通过构造一个一元(t-1)次多项式,如下所示:
f(x)=a1xt-1+a2xt-2+…+at-1x+at
(2)
式(2)中:常数项at为需要分享的秘密,其中t-1个系数a1,a2,…,at-1是GF(p)上均匀选取的随机数.每个子秘密(或称份额)则是取n个不同x值对应的函数值.将这n个子秘密分别发送给n个参与者,只有其中任意t个或者t个以上的参与者合作才能恢复秘密数据,该方案又被称为(t,n)门限方案[13].
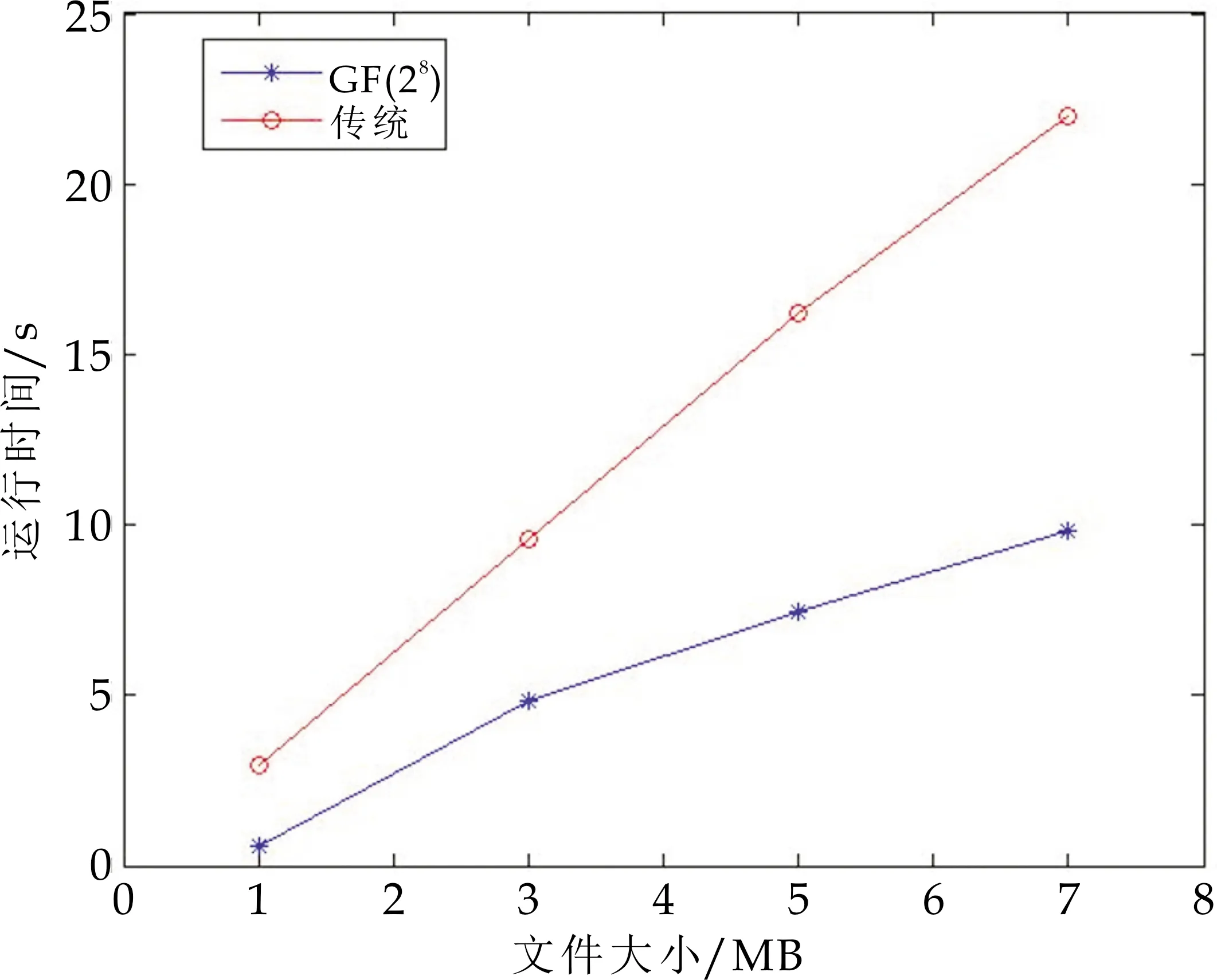
n是参与者的数目,t是门限值,p是一个大素数,要求p>n,并且秘密S小于p,秘密空间与子密钥空间均为有限域GF(p).秘密分发者D给n个参与者pi(0 (1)随机选取一个GF(p)上的t-1次多项式使得f(0)=at=S. (2)秘密分发者D在GF(p)选择n个互不相同的非零元素x1,x2,…,xn,计算yi=f(xi)(0 (3)将(xi,yi)分配给n个参与者,秘密S不公开,每个参与者必须对自己所持有的子秘密(xi,yi)高度保密. (t,n)门限方案在进行秘密恢复时,需要在n个参与者中任选至少t个参与者才可以重构多项式恢复出秘密.每个用户的共享看作是二维平面上的一点(xi,yi),采用Lagrange插值公式构造多项式[6],如式(3)所示: (3) 从而可得秘密S=f(0). 然而参与者仅需知道f(x)的常数项f(0)而无需知道整个多项式f(x),所以仅需式(4)就可求出S,可表示为: (4) Shamir门限方案在进行秘密恢复时,一个多项式只能恢复出一个秘密,在面对大规模秘密数据时效率非常低,而这种新的基于有限域GF(28)的算法可以快速分享大规模数据的秘密. 机密文件可以是文本文件、图像文件或者音频文件,将机密文件按字节(8个二进制位)进行读取,每t个字节为一组,在每组中按顺序以一个字节的数据(GF(28)的元素)作为构建一元(t-1)次多项式f(x)一项的系数,若是机密文件的字节总数不能被t整除,要特殊说明以什么方式补充最后一组文本信息,本课题采取重复前一个字节为补充的方式. 该算法是基于GF(28)有限域的,通过构造多项式f(x)来确定要分发的信息(x,y),里面所有的运算都是在GF(28)里面,此时秘密S不是原算法中多项式的常数项,而是多项式f(x)中的所有系数,不可以公开,通过拉格朗日插值多项式[14]来进行秘密S的重构.该算法由文件分解分发和重构两个阶段组成. 3.1.1 文件分解分存阶段 (1)按组构建一元(t-1)次多项式f(x)=a1xt-1+a2xt-2+…+at-1x+at,x前面的系数分别是原始文件拆分后每一组中一个字节所对应的ASCII值,同时需要选取GF(28)上不可约多项式m(x)为模多项式,比如m(x)=x8+x4+x3+x+1. (2)根据(t,n)门限方案来计算要分发的信息点(xi,yi),yi=f(xi)(i=1,2,…,n)并将(xi,yi)存入相对应文本文件——第i个参与者所持有的子秘密文件,不妨设子秘密文件名为Xi. 3.1.2 原始文件数据重构阶段 若要将机密文件进行数据恢复,在n个文本文件中任意选t个文件其序号相同的数据重构(t-1)次拉格朗日多项式(5),如下所示: (5) 继而得到a1,a2,…,at的信息--原文件中的一组字符. 以“U and Me!”为机密文件的信息来实现拆分和数据恢复,采用(3,5)门限因此每3字节为一组进行拆分,“U and Me!”分成三组“U a”、“nd ”、“ME!”,他们的ASCII值构成三个向量分别为[85,32,97]、[110,100,32]、[77,101,33].在GF(28)域上构建3个不同的一元二次多项式,“U a”对应的多项式为f1(x)=85x2+32x+97,“nd ”对应的多项式为f2(x)=110x2+100x+32,“Me!”对应的多项式为f3(x)=77x2+101x+33.选取不可约多项式为m(x)=x8+x4+x3+x+1,将xi(1≤i≤5)带入多项式中,计算要分发的信息(xi,yi),其中yi=f(xi).下面对f1(x)=(a6+a4+a2+1)x2+(a5)x+(a6+a5+1) modm(x)进行计算,为方便计算不妨令xi=i,得: f1(x1)=(a6+a4+a2+1)·1+a5·1+ (a6+a5+1) modm(x)=a6+a4+a2+1+ a5+a6+a5+1 modm(x)=a4+a2mod (a8+ a4+a3+a+1)=a4+a2:=(20)10 f1(x2)=(a6+a4+a2+1)·a2+(a5)·a+ (a6+a5+1) modm(x)=a8+a6+a4+a2+ a6+a6+a5+1 modm(x)=a8+a6+a5+ a4+a2+1 mod (a8+a4+a3+a+1)= a6+a5+a3+a2+a:=(110)10 f1(x3)=(a6+a4+a2+1)(a+1)(a+1)+ a5(a+1)+(a6+a5+1) modm(x)=(a6+ a4+a2+1)(a2+1)+a6+a5+a6+a5+1 modm(x)=a8+a6+a4+a2+a6+a4+a2+ 1+a6+a5+a6+a5+1 modm(x)= a8mod (a8+a4+a3+a+1)=a4+a3+ a+1:=(27)10 f1(x4)=(a6+a4+a2+1)a2·a2+a5·a2+ (a6+a5+1) modm(x)=(a6+a4+a2+1)a4+ a7+a6+a5+1 modm(x)=a10+a8+a6+a4+ a7+a6+a5+1 modm(x)=a10+a8+a7+a5+ a4+1 mod (a8+a4+a3+a+1)=a7+a6+a2+ a:=(198)10 f1(x5)=(a6+a4+a2+1)(a2+1)(a2+1)+ a5(a2+1)+(a6+a5+1) modm(x)=(a6+ a4+a2+1)(a4+1)+a7+a5+a6+a5+1 modm(x)=a10+a8+a6+a4+a6+a4+a2+ 1+a7+a5+a6+a5+1 modm(x)=a10+ a8+a7+a6+a2mod (a8+a4+a3+a+1)= a7+a5+a4+a+1:=(179)10. 类似的可以计算f2(xi)以及f3(xi)得: f2(x1)=a5+a3+a:=(42)10 f2(x2)=a6+a3+a+1:=(75)10 f2(x3)=a6+1:=(65)10 f2(x4)=a4+1:=(17)10 f2(x5)=a4+a3+a+1:=(27)10 f3(x1)=a3+1:=(9)10 f3(x2)=a7+a6+a5+a2:=(196)10 f3(x3)=a7+a6+a5+a3+a2:=(236)10 f3(x4)=a4+a:=(18)10 f3(x5)=a5+a4+a3+a:=(58)10 进行子秘密的分发,每个参与者的子秘密如下: 第1个参与者所持有的子秘密文件X1为(20,42,9); 第2个参与者所持有的子秘密文件X2为(110,75,196); 第3个参与者所持有的子秘密文件X3为(27,65,236); 第4个参与者所持有的子秘密文件X4为(198,17,18); 第5个参与者所持有的子秘密文件X5为(179,27,58). 根据拉格朗日插值公式 第一组中选取点(x1,y1),(x3,y3),(x4,y4)构成,根据拉格朗日插值公式得: (a5+a3+1)(a4+a2)[x2+(a2+a+1)x+ (a3+a2)]+(a7+a6+a5+a2+1)(a4+a3+ a+1)[x2+(a2+1)x+a2]+(a7+a6+a3+ a2)(a7+a6+a2+a)[x2+ax+(a+1)] modm(x)=a[x2+(a2+a+1)x+(a3+a2)]+ (a7+a3+a2+a+1)[x2+(a2+1)x+a2]+ (a7+a6+a4+a3)[x2+ax+(a+1)] modm(x)= (a6+a4+a2+1)x2+(a5)x+(a6+a5+1) 根据此多项式的系数,将二进制多项式恢复成十进制[85,32,97]恢复出来“U a”这三个字节. 同理可得第二组取(x1,y1),(x4,y4),(x5,y5)构成的多项式为f2=(a6+a5+a3+a2+a)x2+(a6+a5+a2)x+a5根据此多项式的系数,将二进制多项式恢复成十进制[110,100,32]恢复出来“nd ”这三个字节. 第三组取(x2,y2),(x3,y3),(x4,y4)构成的多项式为f3=(a6+a3+a2+1)x2+(a6+a5+a2+1)x+(a6+1)根据此多项式的系数,将二进制多项式恢复成十进制[77,101,33]恢复出来“Me!”这三个字节.就可以得到原来的文本文件中的数据信息“U and Me!”数值算例具体的展示了该算法的步骤,并证明了算法理论的可行性. 3.3.1 算法分析 算法复杂度可分为度量算法执行时间长短的时间复杂度和度量算法所需存储空间大小的空间复杂度.近年来存储技术快速发展,算法在执行过程中所需要存储空间对算法影响逐渐减小,硬件的发展使得较小的代价就可以获得较大的存储容量.因此在本文提出的算法中主要考虑时间复杂度. 所提出的算法的计算资源主要花费在两个部分:子秘密的生成即在给定点处评估多项式和原始秘密的恢复即求解唯一点-值对的系数.整个过程中n表示一个多项式分发的总子秘密数量,t表示门限值,k表示机密文件中总秘密多项式的个数. 在子秘密生成的过程中,f(x)=a1xt-1+a2xt-2+…+at-1x+at是一元t-1次多项式,在给定点xi(1≤i≤n)求f(xi),可以使用霍纳规则[15].霍纳规则是采用最少的乘法运算策略,将一元t次多项式的求值问题转化为t个一次式的算法.求多项式f(x)在x处的值,该算法规则就是f(xi)=at+xi(at-1+…+xi(a2+xi(a1))+…),即计算f(xi)的值需要花费Θ(nt).在秘密恢复的过程中,即是从一组t个点-值对中{(x1,y1),(x2,y2),…,(xt,yt)}确定f(x)的各项系数需要花费O(nlog2n). 3.3.2 实验结果及分析 为了更好的显示算法的实际执行时间,验证本文方案的可行性和有效性,因此使用Microsoft Visual Studio 2013的发行版本编译环境下,使用C语言编程实现算法.实验平台为Inter(R) Core(TM) i5-5257U CPU、8 GB内存、64位Windows10操作系统. 本文构造两组方案加以对比: 一个是基于Lagrange多项式的秘密分享方案——Shamir的(t,n)门限方案,运算在有限域GF(257)上.另一个是本文所提出的基于有限域GF(28)新方案. 实验1:针对同一个门限值,本文选取(3,5)门限的情况下,对大小不同(1 mMB、3 MB、5 MB、7 MB)的文件进行秘密分存和秘密恢复,每一组独立测试分别运行10次,比较他们的平均分存时间和恢复时间,结果如图1和图2所示. 图1 秘密分发的时间 图2 秘密恢复的时间 实验2:针对同一份大小的文件(大小为1.46 MB的英文版哈利波特与凤凰社),不断的增加参与者的个数,记录进行秘密分存和秘密恢复所花费的时间,结果如图3和图4所示. 图3 秘密分发的时间 图4 秘密恢复的时间 通过图1和图2的对比,可以明显地看出,随着机密文件大小的不断增加,传统的方案的时间涨幅较大.同时随着参与者个数的不断增加,传统的方案分发秘密和恢复密码所需要时间有一个明显的变化,尤其是在秘密恢复阶段,因为传统的方案一次只能恢复出一个秘密,在面对这种情况时间就会增加很多.因此,基于有限域GF(28)上的新方案比传统基于插值多项式的秘密分享效率更高.通过程序的验证证明该方案是可以实现的,能够高效的实现机密文件的拆分和恢复,在面对大规模数据和较多的参与者个数比传统的方案耗时更少,效率有所提高,同时在一定程度上实现了文件的分布式存取. (t,n)门限方案中,只有不少于t份子秘密才能恢复出原始秘密数据;而少于t份时无法得到原始秘密数据的任何信息. 对于本课题来说,机密文件以t个字节分组构造一元t-1次多项式,然后计算n个子秘密并分发给n个持有者.因此机密文件大小除以t就是需要构造多项式的个数,假设多项式的个数为k,那么机密文件分解分存后每个持有者将持有k个数据.假设敌手已经得到t-1个持有者的全部数据,通过穷举法去猜测剩余持有者的其中一份的k个数据.由于本算法是在有限域GF(28)上,对于每个数据只能在{0,1,2,…,254,255}上猜测.因此敌手正确猜中的概率为(1/256)k,对于数量级越大的机密文件来说,猜中的概率更小. 本文提出了一种新的机密文件(文本、图片、音频)加密拆分和恢复的方案,通过将文件的字节拆分为t字节一组来构造不同的多项式,根据构造的多项式来确定要分发的点的信息,基于拉格朗日插值公式可以恢复出原始信息,其中所有的运算都是基于GF(28)域上.对于很多领域来说0~255这256个数字也要能组成一个域,但是在有限域GF(P)中,小于256的最大素数为251,于是有限域GF(28)就很好的解决了这个问题,8刚好是一个字节的比特数.有限域GF(2n)上的基本运算涉及到多项式的模乘运算和求逆运算[16],因此GF(28)域比有限域GF(P)上的计算量大且具有相对的复杂性和特殊性,对于破解机密文件增加了一定的难度.同时在计算机中的运算为“异或”运算,这种运算效率非常高,实用性更加高.通过数据实例和程序效率的验证,相比传统基于插值多项式的方法,更为一般化,效率有提升,更适合于大规模数据的秘密分存.2.2 秘密恢复过程
3 基于GF(28)域上的机密文件分解分存与恢复
3.1 算法概述
3.2 数值算例
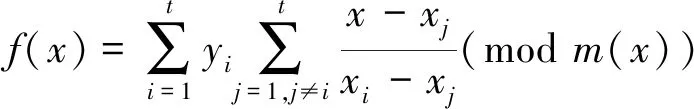
3.3 算法分析与仿真



3.4 安全性分析
4 结论

