Navier-Stokes-Brinkman方程的后验误差估计

高 亮， 李 剑

(陕西科技大学 文理学院， 陕西 西安 710021)

0 引言

多孔介质中流动的模拟有许多应用，包括储层模拟，核废料处理和二氧化碳封存.由于各种原因，这种模拟具有挑战性.首先，区域的不规则性，使模型的几何构建复杂化.其次，地质构造由许多不同的物质组成，具有不同的地质性质.区域内经常出现裂缝和孔洞，改变了有效渗透率.建模这类问题的标准方法是耦合Darcy 和Navier-Stokes，并沿着界面执行BJS条件[1-3].自由流区(裂缝、溶洞)采用Navier-Stokes 模型，而多孔区采用Darcy定律模型[4].然而，在储层中，这两种类型的区域并没有很好地分离，可能很难确定沿界面施加的适当条件.

本文使用Navier-Stokes-Brinkman方程对多孔介质中的流动进行建模，该方程将Navier-Stokes方程和Darcy方程合并为一个方程系统，Navier-Stokes-Brinkman方程根据系数的不同而简化为Navier-Stokes方程或Darcy方程，并提出用它来代替耦合的Navier-Stokes-Darcy方程.通过对系数的选择，该方程可以同时对自由流动和多孔区域进行建模，从而解决沿界面的问题.

本文提出了一种基于残差的后验误差估计方法，并使用该方法对离散化的Navier-Stokes-Brinkman问题进行自适应网格细分，文献中提出了后验误差估计策略[5].与本文工作最接近的是Burda等[6-9]对Navier-Stokes方程的估计,特别是Burda在二维空间中推导的Stokes-Brinkman问题.

1 Navier-Stokes-Brinkman方程

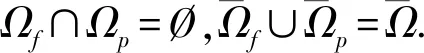
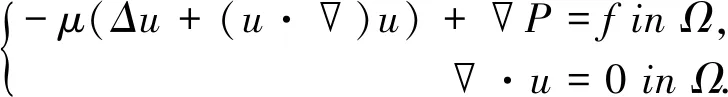
(1)

这里μ为流体的粘度，u为流体速度，p为压力，f为外力.式(1)分别是由动量守恒定律和质量守恒定律导出.在多孔区域Ωp中，流体流动情况受Darcy定律控制：

(2)

这里K表示对称正定的渗透率张量.需要注意的是, 速度u和压力p与Navier-Stokes方程中的相同项不同.在Navier-Stokes方程中，它们表示流体的实际速度和压力，而在Darcy定律中，它们表示一些代表性元素体积的平均值.

在Navier-Stokes-Brinkman方程中，Navier-Stokes方程和Darcy方程组合成统一的方程组：

(3)

这里μ*表示流体的有效粘度.

纳维尔-斯托克斯流和达西流都是Navier-Stokes-Brinkman方程选择适当的μ*和K的极限情况：

(1)μ*=0时，Navier-Stokes-Brinkman方程会退化为Darcy方程；

(2)K-1≫0时，Navier-Stokes-Brinkman方程会退化为Navier-Stokes方程.

由于μ*在多孔区域中对达西定律只有一点微扰的结果，所以可以在整个领域中选择μ*=μ.

Navier-Stokes-Brinkman方程的边界条件选取Dirichlet边界条件，形式如下：

u=0,on∂Ω

(4)

为了寻求方程式(3)和式(4)的解，定义如下空间：

定义X×M上的双线性形式如下：

定义X×X×X上的三线性形式如下：

对于u,v,w∈X，满足

b(u,v,w)=-b(u,w,v),b(u,v,v)=0,

|b(u,v,w)|≤N‖u‖0‖v‖0‖w‖0.

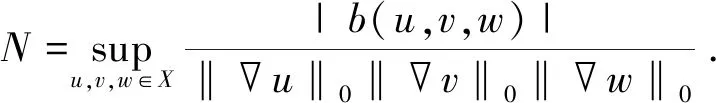
2 非线性微分方程的后验误差估计

记L(U,V)为U到V的连续线性映射，其范数记为‖·‖L(U,v)，I(U,V)⊂L(U,V)为同胚开子集，V的对偶空间V*∶=L(V,R)，设F∈C(U,V*)是一个连续可微函数，DF(u0)表示F在u0处的微分值.

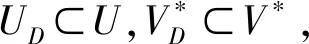
定义Rmin形式如下 ：

2γ-1‖DF(u0)‖L(U,V*)}

对于任意的u∈[B(u0,Rmin)∩UD]，均有下面的结论[10]

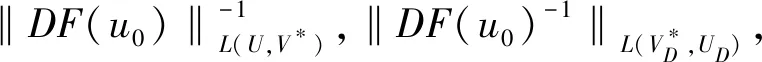
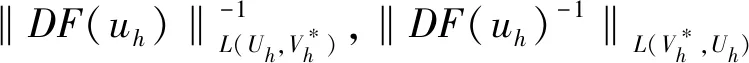
‖F(u)‖S*≤‖DF(u0)‖L(U,V*)‖u-u0‖U

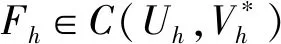
引理3存在常数C1,C2仅取决于定量hk，对于K∈Th,E∈Th,1≤q≤∞(q为向量维数)以下误差估计是有效的[11].

这里Phv是v的插值逼近函数，Th是一个有限元剖分，K是有限元剖分的子单元内部，E是有限元剖分的子单元公共交界.

3 Navier-Stokes-Brinkman方程后误差估计

本节构造了Navier-Stokes-Brinkman方程的误差估计.令

定义式(3)和式(4)的变分形式如下：对于任意(v,q)∈X×M

〈F([u,p]),[v,q]〉:=μ((u,v)+

K-1(u,v)+((u·)u,v))-

(p,·v)+(q,·u)-(f,v)=

a(u,v)-d(v,p)+d(u,q)+

b(u,u,v)-(f,v).

(5)

使用混合有限元离散式(5)，并且构造离散的速度空间Xh⊂X和离散的压力空间Mh⊂M如下：

其中P1(K)表示一次多项式，P2(K)表示二次多项式.P2-P1有限元对满足LBB条件

则问题的离散化是稳定的.

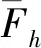
(6)

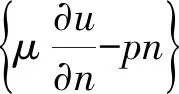
3.1 能量范数的后验误差估计

本小节主要介绍能量范数中速度和压力的后验误差估计.定义局部误差指示子如下：

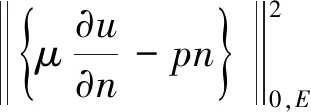
定理1记(u0,p0)是式(2)和式(3)的弱解，(uh,ph)是利用P2-P1元所求的逼近解，且满足

〈F([uh,ph]),[vh,ph]〉=0,

则有如下估计：

证明：首先，证明F的导数的存在性，以及它在(u0,p0)∈X×M的邻域中是连续的.

(u0·)uv+(u·)u0v)-p·v+

q·u]dx=a(u,v)-d(v,p)+d(u,q)+

b(u0,u,v)+b(u,u0,v),

由上述定义可知

〈F([u,p])-F([u0,p0])-DF([u-u0,p-

因此

故F是可微的.接下来，证明DF是Lipschitz连续的.

记DF1(·)为DF在[u1,p1]处的导数.对于任意(v,q)∈Q，(u,p)∈B([u0,p0],R0)有下列估计成立：

〈DF1([u,p])-DF0([u,p]),[v,q]〉=

2N‖(u1-u0)‖0‖u‖0‖v‖0≤

2N‖[u1,p1]-[u0,p0]‖P‖[u,p]‖P‖v,q‖Q

由上式可得

2N‖[u,p]‖P≤2N(‖[u0,p0]‖P+R0)≤γ

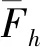
取(vh,qh)∈Xh×Mh，

〈F([uh,ph])-Fh([uh,ph]),[vh,qh]〉=0

因此，

将上述不等式结合得到所证结论.

3.2 L2范数的后验误差估计

对于速度的L2范数，考虑如下线性化问题.寻求(φ,ξ)∈X×M,(u0,p0)是原问题的弱解，对于某些给定的g∈Y和任意(v,q)∈X×M，使得

a(φ,v)-d(φ,q)+b(u0,v,φ)+

b(v,u0,φ)+d(v,ξ)=(g,v)

(6)

可知双线性形式a(φ,v)-d(φ,q)+d(v,ξ)是连续的.由于Necas定理，上式有唯一的对偶解(φ,ξ)∈X×M，且满足

‖φ‖2,Ω+‖ξ‖1,Ω≤C‖g‖0,Ω,

这里，

δK=hK‖·uh‖0,K,

定理2令(uh,ph)是(u0,p0)的近似，在定理1的条件下，可得结论如下：

证明：取v=g=u0-uh,q=p0-ph代入式(6)，可得

d(u0-uh,ξ)+b(u0,u0-uh,φ)+b(u0-

uh,u0,φ),

另一方面，由式(5)及其离散形式作差可得

a(u0-uh,vh)-d(vh,p0-ph)+d(u0-uh,qh)+

b(uh,u0-uh,vh)+b(u0-uh,uh,vh)=0,

将上述两式求和，并令(vh,qh)=(Phφ,Phξ),

Phφ,p0-ph)+d(u0-uh,ξ-Phξ)+b(u0,u0-

uh,φ-Phφ)+b(u0-uh,uh,φ-Phφ)+b(u0-

uh,u0-uh,φ)=(f+μ(△uh-(uh·)uh-

K-1uh)-ph,φ-Phφ)-(·uh,ξ-Phξ)+

uh)·)(u0-uh),φ)≤

由上式可得速度的L2范数的误差估计.

4 数值算例

本节中，使用两个数值算例去证明本文理论结果的正确性，并且验证了通过后验误差估计法所得到的误差指示子对于Navier-Stokes-Brinkman方程自适应过程的有效性.自适应网格算法如下：

给定一个网格剖分Th，并计算出每一个子单元K所对应的误差指示子ηK，再给定一个常数θ∈(0,1).

(2)如果ηK≥θηT,max，则对单元K进行网格加密.加密后得到一个新的网格剖分，返回步骤(1).

注：在自适应过程中，有些单元需要进行粗化处理，其基本思想是将误差太小的单元聚集在一起.

4.1 圆形区域的数值算例

第一个算例中流体所在的区域为半径为1的圆盘，圆心与边界之间有一条裂纹.从初始的网格剖分图1(a)开始自适应计算，经过两次迭代计算得到了如图1(b)所示的网格剖分，然后再经一次迭代计算，结果如图1(c)所示.图2所体现的是由于在裂纹处的自适应迭代计算，压力线的剖面变得更加光滑，这也意味着计算结果更加精确.

(a)初始剖分 (b)自适应迭代两次 (c)自适应迭代三次图1 P2-P1有限元对在圆形区域自适应过程

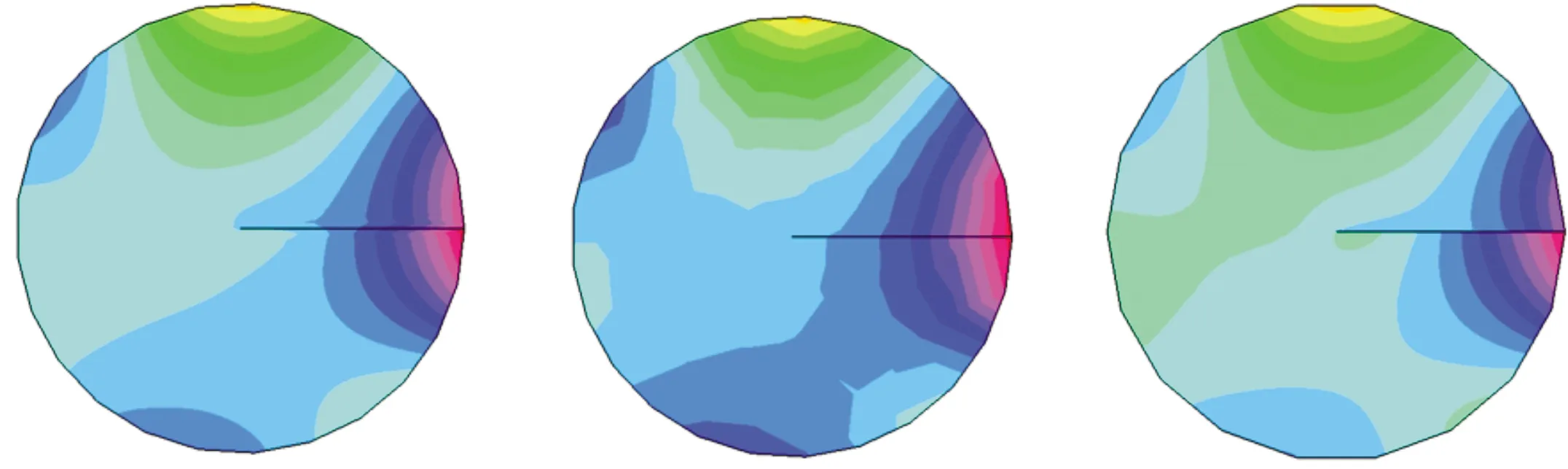
(a)初始剖分 (b)自适应迭代两次 (c)自适应迭代三次图2 P2-P1有限元对在圆形区域自 适应过程中压力线变化

4.2 L形区域的数值算例

第二个数值算例中选取了L型区域Ω=(0,1)×(0,0.5)/(0,0.5)×(0.5,1)，并且边界为Dirichlet边界条件，进行自适应迭代计算，得到如下结果，从初始的网格剖分图3(a)开始自适应计算，经过两次迭代计算得到了如图3(b)所示的网格剖分，然后再经一次迭代计算，结果如图3(c)所示.通过在拐角处进行自适应迭代计算，网格剖分在拐角处进行了加密，计算结果更加精确；同时也避免了因统一加密而导致的计算量的增加.图4所体现的是由于在拐角处的自适应迭代计算，压力线的剖面变得更加光滑，这也意味着在计算量小的前提下，得到了更加准确地表示.

(a)初始剖分 (b)自适应迭代两次 (c)自适应迭代三次图3 P2-P1有限元对在L型区域自适应过程

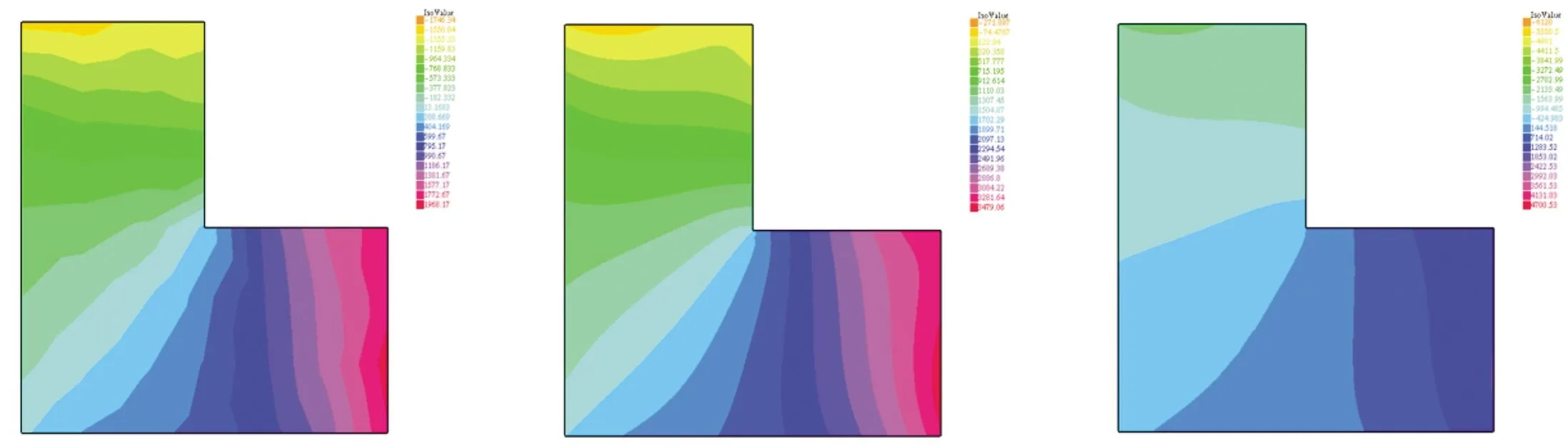
(a)初始剖分 (b)自适应迭代两次 (c)自适应迭代三次图4 P2-P1有限元对在L型区域自 适应过程中压力线变化

5 结论

本文在混合有限元法的基础上，推导出了Navier-Stokes-Brinkman问题的残差型后验误差估计，得到了可计算的能量范数全局上界以及速度的L2范数的误差估计值，并且利用计算所得的估计值驱动自适应算法去求解Navier-Stokes-Brinkman问题，通过数值算例，证实了理论的正确性以及算法的高效性.