轴编C/C复合材料性能预示及细观参数优化研究

王春光, 朱 涛, 唐 敏, 曹 鹏

(1.陕西科技大学 电气与控制工程学院， 陕西 西安 710021； 2.中国航天科技集团公司第四研究院 第四十一所， 陕西 西安 710025； 3.中国航天科技集团公司第四研究院， 陕西 西安 710025； 4.北京工业大学 建筑与土木工程学院， 北京 100124)

0 引言

C/C复合材料，即碳纤维增强碳基体复合材料，是二十世纪50年代后期发展起来的一种增强相和基体相均由具有特殊性能的纯碳组成的结构复合材料[1,2]，它具有比强度高、热稳定性好、以及耐磨、抗烧蚀等一系列优异性能，特别是其力学性能随温度升高强度不降反升的特性，使其在航空、航天领域得到了广泛应用[3,4].由于C/C复合材料的内部微观结构非常复杂，尤其是孔隙率、裂纹、孔隙均值、孔隙形状等特征参数分布域较宽，有限的实验数据还难以建立起微结构特征和材料性能的全面关系.为此，需要研究准确的理论预示方法，并经过前述实验验证，从而获得微结构特征与整体及组分性能的相关关系[5-7].

自20世纪80年代以来，国内外对编织复合材料性能的预测研究进行了大量的工作，刚度性能的研究已经比较完善，文献[8-11]介绍了当前国内外针对编织复合材料力学性能预测的一些方法.随着有限元技术的发展，结合均匀化方理论的性能预示方法为开展复合材料的性能预示提供了新的思路[3,12-14].而由张卫红导出的基于能量法的复合材料线胀系数预示方法因简单实用、精度较高，也在国内逐步得到推广[15].遗憾的是目前国内的力学分析中采用的组分性能大部分是组分材料的原始性能，即使测得了部分材料的原位性能，但是由于实验设备及方法的本身误差，测试结果的有效性大打折扣.导致使用组分材料原始性能预报的C/C复合材料宏观性能和实验结果产生较大的偏差.

本文将均匀化方法和有限元方法相结合，同时引入能量法，建立了材料宏观性能的预示方法.利用Python生成满足微结构特征分布规律的基体、界面和纤维棒(束)几何模型，对细观组分的弹性性能进行预示.将预示结果与部分实测结果对比，厘定各组分材料的数值计算输入参数.以材料的单胞模型(RVE)为基础，引入周期性位移边界条件，预示了轴编C/C复合材料的等效弹性性能及材料的等效线胀系数[16-19]，并与部分实验结果对比，验证了预示方法的准确性.通过对具有不同编织间距和纤维棒直径的材料模型的宏观性能进行预示，获得了该材料的最佳编织方式，为材料的工艺优化及合理应用提供参考.

1 轴编C/C复合材料力宏观性能预示方法

1.1 复合材料的均匀化过程及刚度预示方法

基于均匀化方法进行复合材料刚度的预示已经得到国内外学者的广泛认可，其概念如图1所示.为了解决大规模的宏微观联合计算的困难，引入微元概念.微元在复合材料结构中代表一个点，它的平均应力和应变关系被看作复合材料有效本构关系，实际上是将非均匀的微元用一个具有上述平均应力和应变关系的均匀化材料来代替，对复合材料结构的每一点都运用上述概念，这样原本对非均匀复合材料结构分析的问题转化为对一个均质化后相同结构进行分析的问题.该均质化结构的材料具有复合材料有效宏观本构，这样使原问题大大简化.

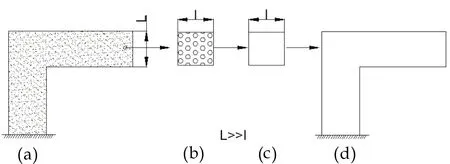
(a)原结构(b)微元(c)微元均匀化(d)均匀化结构图1 复合材料结构、代表单元和等效结构

轴编C/C复合材料的等效弹性刚度矩阵见公式(1)，具体推导过程及含义详见文献[3,13,14].

(1)

1.2 基于能量法的复合材料热膨胀性能预示方法

能量法的基本思想是：利用微结构和均质等效体的关系，通过推导复合材料等效性能与微结构变形能量的关系，得出复合材料的等效性能的能量表达式[15].

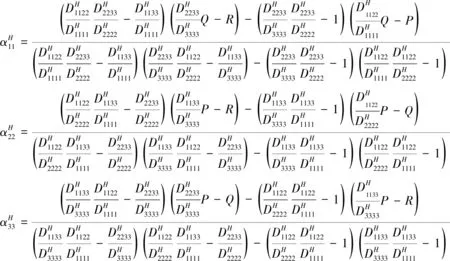
(2)

式(2)中:

1.3 边界条件

由均匀化方法的推导过程可知，均匀化方法的一个主要假设是周期性条件，这要求在进行有限元计算及求解过程中，胞元位移应满足周期性边界条件[13].对于具有空间平移对称性的周期性单胞结构，其位移的周期性条件可以表示为：

(3)

2 RVE单胞的建立及组分性能厘定

2.1 RVE模型建立

轴编C/C复合材料的RVE单元是由纤维棒、纤维束、基体和界面所组成的长方体结构，其编织结构及各组分相尺度如图2所示，采用拉挤成型的细碳纤维刚性棒构成轴向增强网络，并采用软碳纤维纱编织成预织体，纤维棒在轴向按正三角形摆列，纤维束依次穿过纤维棒形成的0 °、60 °和120 °三个通道形成层间增高，如此循环往复直至形成所需尺寸的预织体.预织体经沥青浸渍、炭化、致密化工艺及高温处理制成高密度4D C/C复合材料.这种预织体的最小单元具有沿轴向的对称轴，且其编织厚度沿轴向累加，因此称其为轴编C/C复合材料.

基于单胞模型，构建的轴编C/C复合材料有限元模型如图3所示.网格的划分和后续周期性边界条件的施加有关，因此需要严格保证单胞对应面网格节点一致.本文采用C3D8和C3D6单元对纤维棒、纤维束和基体进行离散；对纤维棒/基体界面，纤维束/基体界面全部采用八节点C3D8单元进行离散.网格数目共计50万.

图2 轴棒法C/C复合材料的RVE单元

(a)RVE有限元模型

2.2 组分性能厘定

2.2.1 基体和界面的物理力学性能

对于C/C复合材料基体和界面均可将孔隙和裂纹看成是在纯炭基体内部的夹杂，所不同之处在于基体和界面的微结构的形状和尺度具有一定的差异.本文采用python语言编程随机生成满足二者微结构特征客观分布规律的几何模型，并采用均匀化方法进行计算，这种方法可以考虑孔隙、裂纹之间的相互影响.

为了既简化计算量又包含足够的孔隙信息，基体的计算模型边长为0.4 mm，界面的边长为0.02 mm，所生成的模型如图4(a)、(b)所示.模型中孔隙以椭球型为主，个别位置椭球长短轴比值较大，形成裂纹，孔隙尺度、分布和含量由前期试验对不同批次材料统计获得.前期采用纳米压痕实验获得无空隙基体模量为12.34 GPa，泊松比为μ=0.23，作为计算参数输入.

(b)界面微观孔隙及几何模型图4 基体及界面性能计算模型

根据数值计算结果获得基体和界面的弹性性能随孔隙率的变化规律，如图5所示.图5(a)为孔隙率对基体弹性性能的影响，可以看出基体的弹性性能随孔隙率呈线性变化，孔隙率增加，导致弹性模量和泊松比均减小.图5(b)为孔隙率对界面弹性性能的影响，可以发现孔隙率对界面弹性性能的影响趋势与孔隙率对基体的影响相同.

根据前期试验统计获得材料标样的基体孔隙含量为0.036，从图5(a)获得模量和泊松比分别为11.5 GPa和0.227 9.根据前期试验统计获得材料标样的界面孔隙的含量为0.25，从图5(b)获得模量和泊松比分别为3.91 GPa和0.12.

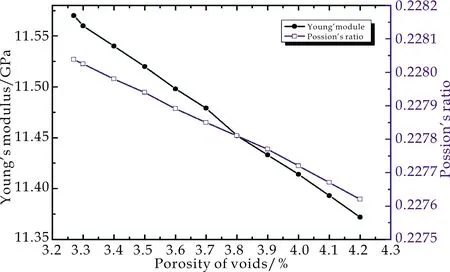
(a)孔隙率对基体刚度性能影响

(b)孔隙率对界面刚度性能影响图5 孔隙率对基体和界面弹性性能的影响

2.2.2 纤维棒和纤维束力学性能

本节基于纤维棒(束)的微结构特征及其随机性分布，采用有限元方法并结合Python语言编程生成满足微结构特征分布规律的纤维棒(束)几何模型，并利用均匀化方法，对其刚度性能进行预示.图6为纤维棒的几何模型，模型由纤维单丝、基体及孔隙组成.

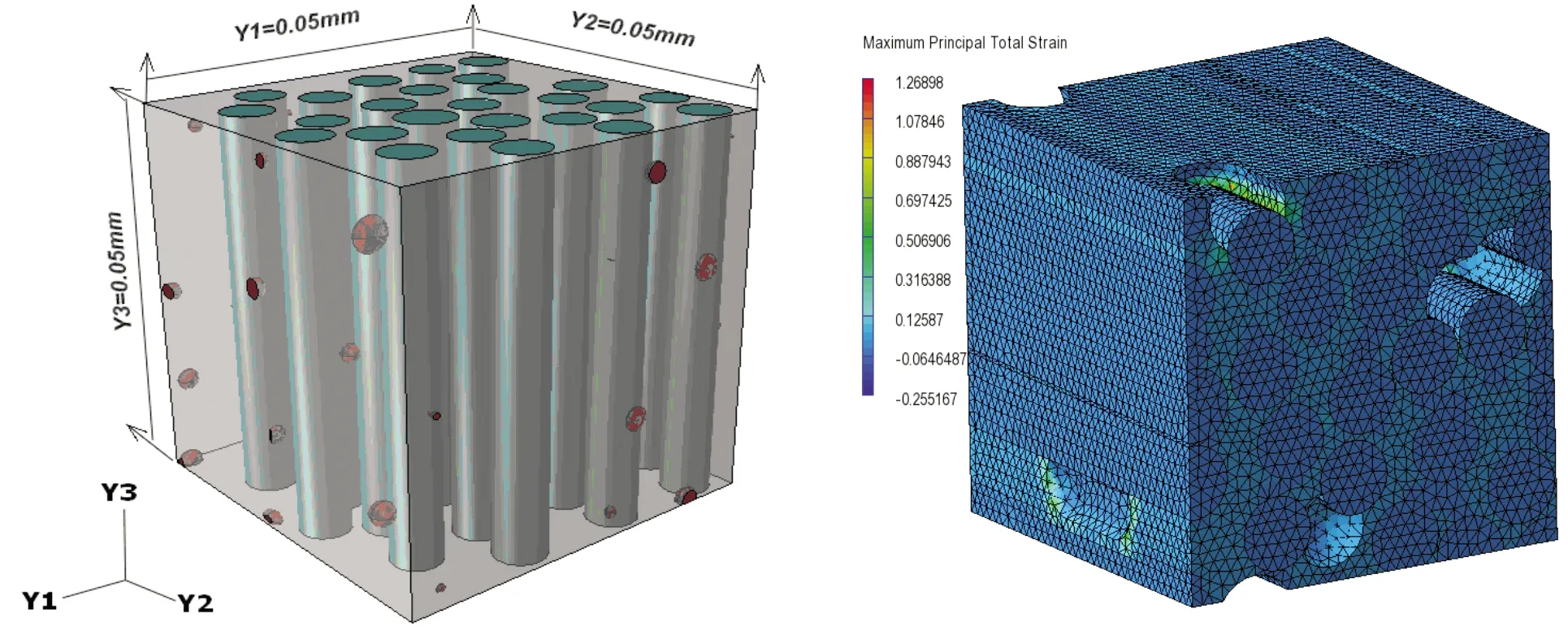
(a)几何模型 (b)有限元模型图6 纤维棒(束)几何模型及有限元模型

本文以相关实验为基础，结合文献[13]和[14]，确定纤维单丝和基体的输入参数如表1所示.增强相内的无空隙基体弹性参数采用与上一节相同的纳米压痕试验结果.

表1 增强相内纤维和基体刚度参数

通过有限元模型计算增强相的刚度性能，计算结果表明即使存在少量的孔隙，增强相仍表现为横观各向同性，表2列出了增强相的计算结果，以及前期部分实验结果.从表2可见，纤维棒的拉伸模量预测误差为13.4%，压缩模量预测误差为13.7%，剪切模量的预测误差为10.4%，验证了增强相的计算方法是可信的.在此后的材料宏观性能的计算中，增强相的纵向性能按实验值给定，而剪切性能和其它未测参数按预示值给定.

表2 增强相刚度性能

3 计算结果及分析

3.1 弹性性能计算结果

利用轴编C/C复合材料的单胞模型，施加周期边界条件得到其有效性能如表3所示.通过对不同状况下的预测结果和实验结果的对比，可以发现数值预测结果的弹性模量与实验基本相符，从而检验了预测方法的有效性.

表3 轴编C/C复合材料力学性能

3.2 热胀系数计算结果

基于2.2节所得组分材料参数，采用能量分析法对单胞模型的热膨胀性能进行预示，其预示结果和实验结果的比较如表4所示，表中的热膨胀实验数据采用DIL 402热膨胀仪进行测试，试样尺寸为φ60 mm ×50 mm.

通过预示结果和实验结果的对比表明，基于能量法的热膨胀系数预示方法具有一定的预示精度，但两个方向的预测值均比实验值大，这可能是由于基体的热膨胀系数取值大于真实值所致.

表4 轴编C/C复合材料常温热膨胀系数

3.3 编织间距对轴编C/C复合材料刚度和热膨胀性能的影响

改变纤维棒中心间距，进行材料的刚度和线胀系数预示，所获编织间距对拉伸模量和线胀系数的影响如图7所示.随着编织间距的增加，轴向和径向的拉伸模量和热膨胀系数均逐渐降低.其主要原因在于，随着编织间距增大，在RVE内轴向纤维棒和径向纤维束的体积含量均降低，而基体的体积分数增加.由于基体的模量和热膨胀系数较纤维棒和纤维束都低，当其体积分数增加后，必然引起模量和热膨胀系数的整体下降.

从轴编C/C复合材料的使用环境来看，需要以降低模量和热膨胀系数来降低其作为结构件时的热应力，如此，则必然希望材料的编织间距增大，然而研究表明纤维体积分数与材料的抗烧蚀性能密切相关，当纤维体积分数减小时，材料的烧蚀率增加.因此，轴编C/C复合材料的编织间距的优化应当结合材料的烧蚀性能进行分析.

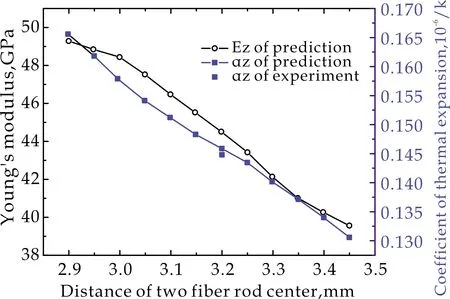
(a)轴向方向

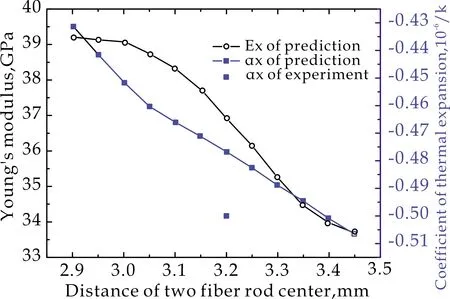
(b)径向方向图7 纤维棒中心间距对轴编C/C复合材料 轴向、径向拉伸模量和热胀系数的影响

3.4 纤维棒直径对轴编C/C复合材料刚度和热膨胀性能的影响

图8给出了纤维棒直径对材料拉伸模量和线胀系数的影响.从图8(a)可以看出，随着纤维棒直径的增加，轴向拉伸模量显著提高，而热膨胀系数显著降低.这主要是因为，在编织间距不变的情况下，纤维棒直径增大，显著增加了单胞中轴向纤维的含量，又由于轴向纤维的轴向模量较高，而轴向热膨胀系数小于横向热胀系数，从而导致材料在轴向模量的升高和热膨胀系数的降低.

从图8(b)可以看出，径向拉伸模量和热膨胀系数均是纤维棒直径的增函数，但增量较小.其原因在于，对于径向拉伸模量，当编织间距不变时，在不改变纤维束自身尺度的情况下，增加纤维棒直径不会引起径向纤维束的体积分数变化，但是将会导致基体的体积分数减小，由于基体的模量较纤维棒的横向模量小，故而导致材料的径向拉伸模量有所增加.对于热膨胀系数，由于基体的热膨胀系数较纤维棒的横向热膨胀系数小，当纤维棒体积分数增加，基体的体积分数减小时，纤维棒横向热膨胀系数对材料径向热膨胀系数的增加大于基体对径向热膨胀系数的减小所致.

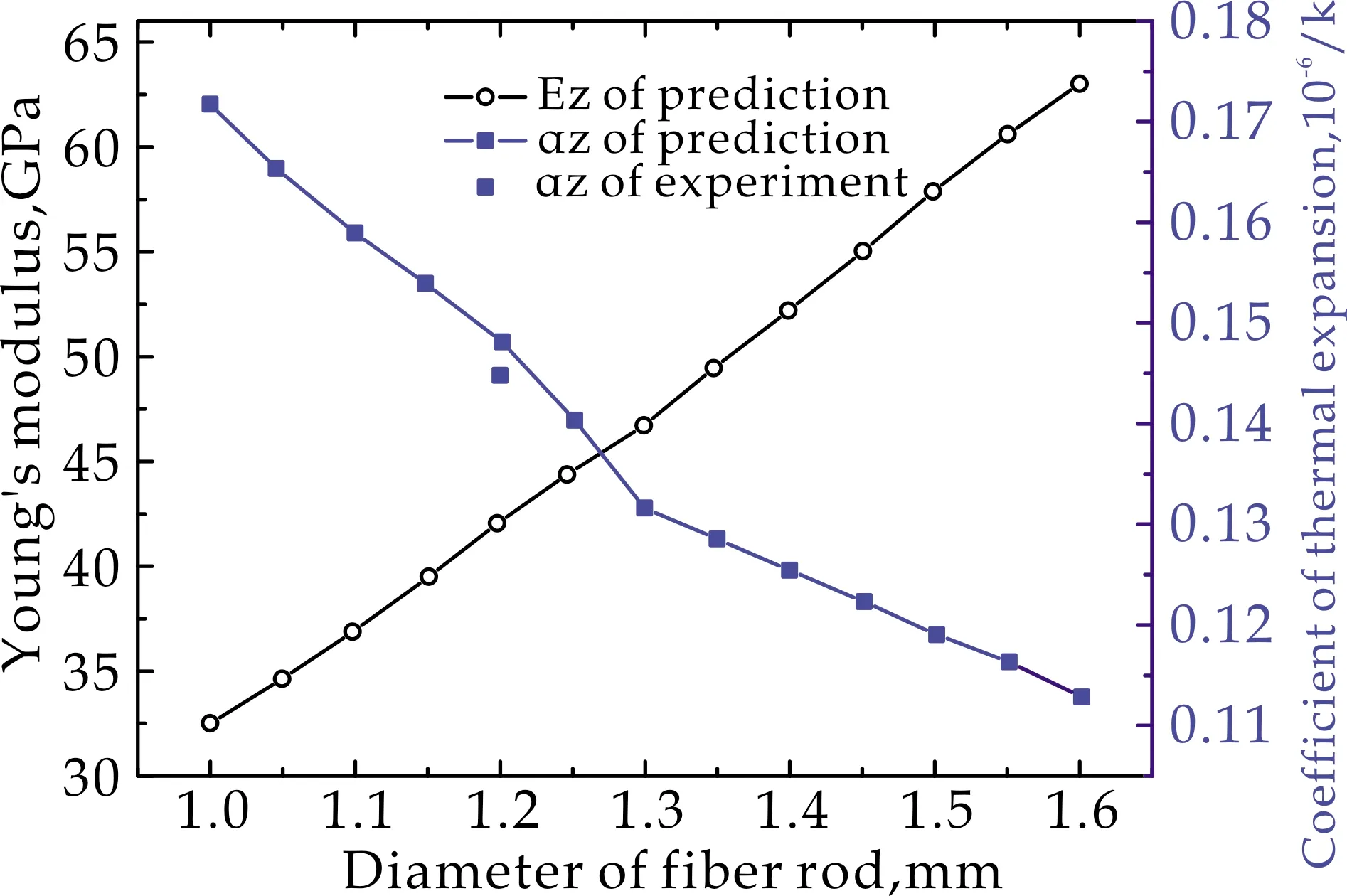
(a)轴向方向

(b)径向方向图8 纤维棒直径对材料轴向、径向拉伸 模量和热胀系数的影响

4 结论

本文获得如下结论：

(1)采用有限元方法并结合Python语言生成满足微结构特征分布规律的界面和基体几何模型，计算基体和界面的弹性性能，计算结果表明孔隙率对基体和界面的弹性性能有较大的影响.可以看出基体和界面的弹性性能随孔隙率呈线性变化，孔隙率增加，导致弹性模量和泊松比均减小.使用同样方法，计算增强相的弹性性能，计算结果表明即使存在少量的孔隙，增强相仍表现为横观各向同性.与前期部分实验结果对比发现，纤维棒的拉伸模量预测误差为13.4%，压缩模量预测误差为13.7%，剪切模量的预测误差为10.4%.验证了基于有限元方法获得材料组分性能的方法是可信的.

(2)基于均匀化方法和能量法，并结合有限元技术，以轴编C/C复合材料的单胞模型为基础，对材料的刚度和热胀系数进行了预测.发现数值预测结果与实验基本相符，从而证明了预测方法的有效性.通过计算不同编织结构和纤维棒直径条件下的宏观刚度性能和热胀系数，建立了细观参数和宏观性能之间的关系.计算结果表明，随编织间距增加，材料的拉伸模量和导热系数均有所减小；随纤维棒直径增大，材料的拉伸模量均增大，轴向热胀系数减小，径向热胀系数增大.