用球体分割法解决最大平面图“四色问题”

浙江省宁波市奉化公路运输有限公司 焦永溢

最大平面上的任何一个三边形都可拉大成为最外面的一圈。如果在最大平面图中间的某个三边形中又存在一个或多个的点，就是说这个三边形的外面与里面都是有许多的点。这种情况下仍旧可把这个三边形拉大到球的最大圈（赤道）上，这个三边形外面的点与里面的点就分别成了南北半球上的点。如果沿着这三边形的这一圈线（也就是赤道）把球切成两半，除了这三条线和三个点分别属于两个半球所共有，其他的点和线就南北分开，各不相干。而半球体与球体在拓扑上是完全一样的，就是说可以把原来的一个球体分割成为各自独立的两个球体，接下来分析各点如何着色，就完全是在两个各不相干的球面上分析了。如果这分开来的球面上又有这种三边形中包含一个或多个点的现象出现，又可重复上述操作，把三边形外的点与内的点分割开来，成为各不相干的两个球，一直能分割到每个球上再没有这种三边形内外都有点的状况。这就好比一个芋头上长出一个甚至多个芋子来，可以把这些芋子掰下来单独成为球体来看待，芋子上如再长出芋孙，也可把芋孙掰下来单独成为一球体；子球可以大于母球，所以各球之间不分母子，更可以看成是连体儿，把各球分割开来好比是给连体儿做分离手术。

其实除了三边形内外都有一个或多个点的情况，一边形（就是只有一个点，比如地球上的海洋）分别包围一个或多个点（比如地球上各个岛和陆地）的情况；还有二边形（就是二个点相互有二条连线）内外分别包含一点或许多点的情况。这两种情况也可用与上面相同的方法，沿这个点或二边分割成两个各自独立的球。

前一种海洋与每块陆地或岛屿可单独成为一个球体，每个球体上的海洋这一点是共同拥有的，合在一起时就相当于若干个子球与母球都是点接触，分割开来后除了这一点是共同点，其余各球之间的点都是互不相干的。这个分割手术后只留下一点作为创口，可以忽略不计。

后一种沿二边形分割后，属于两球共有的这二个点二条线中间是没有点了，可把这二条边看为一条，这个子球与母球合在一起时只是二点二线一面接触，而分开后二线可合为一线，一个面也就消失。这个分割手术后只留下一条线作为创口，也是可以忽略不计的。

沿三边形分割球体，分割后属于两球共有的是这三个点、三条线和一个三边形，这两球体之间就是以这个三边形为接触面的面接触，这三边形也就是这个分割手术后留下的创口。这个三边形的小创口已经是最小的创口了，整个球面上全是三边形，全是这样的最小创口，这最小的创口存在与否，不会影响整个图的性质，也是等于没有创口。规范标准的最大平面图，就是全图全由三边形组成，并且再没有三边形中还有点的情况，因为一旦有这种情况，又要沿这三边形分割了。

能不能把大于三边的一圈当赤道来分割成两个半球呢？只要分割后在两个各自的球面上把这个多边形的创口作适当的处理，同样也是行得通的。那么下面就来说一下这个多边形的创口该如何处理。

为了避免分割切口周围的点之间有连线（就是我在用“减少法”证明“四色问题”时所说的“短路现象”），必须遵循一个原则，要先处理全图中度数小的点。图论里已经有一个定理：最大平面图中度数最小的点，一定是等于或小于五度的。上面的球体分割法已经把一度、二度、三度的点都当小芋子切割下来了，这样就只要分析四度和五度的点该如何切下并处理创口就行了。

对于四度的点，如果沿着包围它的一圈当赤道切割下来，两半球的接合面就会形成四边形的一个创口。如果用中间加一点，再与四边形四个顶点画连线的方法处理这个创口，割下小的子球等于四棱锥的底面中加一点再与面上的四个点画连线，就成了一个六个点（每点都是四度）、十二条线、八个面的多面体。而分割后的母球的创口处理后仍旧成了原样，等于白白切割了这一刀。所以在处理这个四边形的创口时不能这么操作，而是应该以其中一条对角线为对称轴，把对称轴两边所对应的点和线合并到一起（其实就是我的“减少法”中的合并方法），只要这四边形的四点间没有短路现象，就可以这么操作。这样处理创口后，割下来的子球就成了这面两个相邻的三边形、反面也两个相邻的三边形的扁平四方片。而割下来的母球上，创口上的点和线合并后，这没合并的对称轴两端的这两点的度数都是减少了二度（见图1左边A点和C点），下一步就可以再继续找球面上度数少的点进行这样的操作。两个球的共同部分（切割后的创口）从四个点、四条线合并成了三个点A、B（D）、C和二条线AB（D）、B（D）C。两球上只要A、B（D）、C这三点着色时对应相同，其他各个球上的点就可各自处理了。

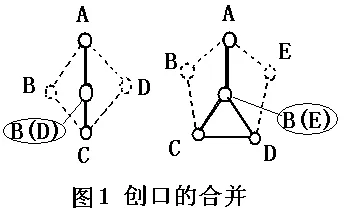
对于五度的点，如果也沿着包围它的一圈切割下来，两个半球的接合面就会形成五边形的一个创口。如果也用中间加一点，再与五边形五个顶点画连线的方法，同样也是白白切割了这一刀。这时也需要用我的“减少法”中的合并方法来合并周围的点，因为周围的点是奇数，不可能完全把对称的点合并，还要剩下一个三边形，只要这五边形外围的点之间没有短路现象，也可以这样操作的（图1 的右边）。这样处理创口后，割下来的子球就成了一个三棱锥，再在一条棱上长一个三边形的薄片，仿佛背上长鳍的一条鱼。而割下来的母球上，创口上的点和线合并处理后，没合并的三个点A、C、D度数都是减少的，下一步又可以继续在球面上找度数少的点进行这样的操作。两个球的共同部分（创口）从五个点、五条线合并成了一个三边形B（E）CD再加上一个点A和一条线AB（E）。两球上只要这三边形的B（E）、C、D这三个点及外加的A点着色时对应相同，其他各个球上的点也可以各自处理了。

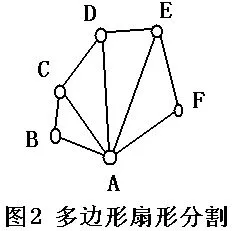
上面的这两种合并的方法就如在连体儿分离切割手术后对创口的缝合，还有一种更加简单的操作不用这样的缝合，而是在多边形的创口上采用另一种扇形分割法。如图2 所示，在把这个球面上的多边形分割为三边形时，不是用前面的中间加一点，再向周围各点画连线（仿佛中心点向外放射光芒状）的方法，而是从其边上的一个点A向其余各点画连线（仿佛展开的折扇状）的方法。这种折扇形分割法，把多边形分割成三边形时，球面上点数没有合并减少，但线数是减少的（这个射线出发点两旁的点B和F不用画连线，度数一定比分割前要小）。分割开来的两球多边形创口上，都对应地这样做创口处理，这个射线出发点A用一种颜色，其余B、C、D、E、F各点依次用第二和第三种颜色（周围点数是偶数时A点可与C、E同色只要二种颜色就够了）。用这种处理方法，两球分割开来的共同多边形，就变成了连在一起的几个三边形，只要这几个共有的三边形上的对应点着色相同，两球上其余互不相干的各点就可以在各自的球上自行处理。做好了以上这一步后，又可在球面上找度数最少的点进行这样的切割操作。

通过以上的分析，不但点接触、线接触以及三边形面接触的两球体可分开来分析，有着更大的共同多边形相连的两个球也可分割，就是说不一定从葫芦形细小的地方来分割，可以从任何一个圈切开来，就连原来没有明显葫芦状的任何球的变形体，前提只要是连线能围成圈，并且这圈上的点之间没有短路现象，就可沿着这一圈线切割下来。这样切割后，只要两个球切割面多边形上的对应的点，作相同的划分成三边形处理，一直是可以一步步切割下去的，直到每一小块上的点数少于等于四为止。就像一个芋头上的大小芋子可以切割下来，每一个芋子上的芋孙也可以切割下来，并且在每个单独的球体（芋头或芋子、芋孙）上还可以下刀切割（前提是切口多边形的周围点之间没有短路，切下后两个球体上的创口要作对应相同的最大化（也就是多边形分割成三边形处理），就如把大的芋头或芋子、芋孙再切为几块，一直切到每一小块上的点只剩四点和四点以下，这样每一块都是四种颜色够了。反过来操作，把每一块着四色的碎芋块（包括分割开来的芋子及碎块），拼合起来就能成为大的芋头和芋子的结合体。每个小块四色足够了，整个拼起来的球面体也就四色足够了。这个结论就是任何复杂的球形多面体，都可由许多块四点及四点以下的多面体拼合组成，而每一小块的点只要四种或四种以下颜色组成，整个合成后也是只用四种颜色就够了。也就是说，我最早写的《关于“四色问题”的证明》和《彻底解决“四色问题”》两篇文章中的分析是对的，任何复杂的最大平面图，都是由许许多多的三边形及三点包围一点图形所组成。