数学解题要“多想少算”
◇ 浙江 王加义
同一个数学问题,学生切入的角度不同,解答的方法也不尽相同,但有的方法烦琐,有的方法简捷,对于选择题的求解,简捷的方法往往可以“一望而答”.这些简捷方法源于对题目条件的仔细审视,对问题本质的深入挖掘,即通过“多想”达到“少算”的目的,这也是高考对考生的重要考查内容.
1 利用函数性质,局部判断
①f(x)是偶函数;
③f(x)在[-π,π]有4个零点;
④f(x)的最大值为2.
A.①②④ B.②④
C.①④ D.①③

因为f(-x)=sin|-x|+|sin(-x)|=sin|x|+|sinx|=f(x),所以f(x)为偶函数,f(x)在[-π,π]的图象如图1所示,故可利用x>0时,f(x)的性质进行判断.

图1
如图1,因为f(0)=f(π)=f(-π)=0,所以f(x)在[-π,π]有3个零点.故①④正确,选C.

本题若直接求解,分类讨论的标准不易确定,而利用函数的奇偶性和周期性,只需对函数的局部性质进行研究,从而简化了思维过程.
2 利用图形差异,过滤错选
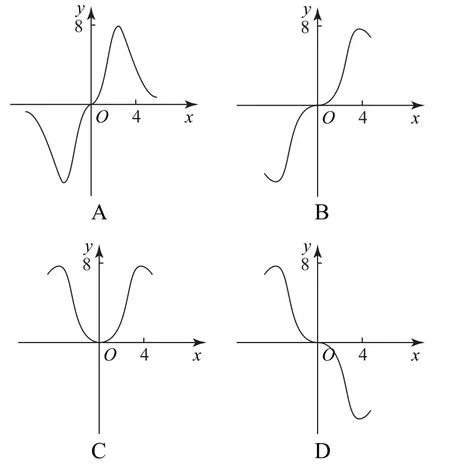


给出函数关系式,判断函数图象,是近年高考全国卷中的常考题型,此类问题求解中需先结合函数的奇偶性、单调性等进行判断,再结合各选项所给图象的差异特征进行筛选,得出正确图象.
3 结合运算关系,以“形”破“数”
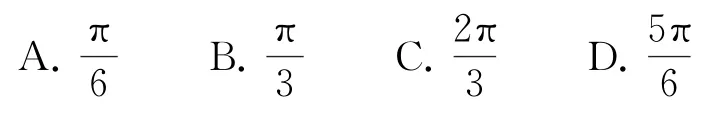

根据题目条件(a-b)⊥b 可构造直角三角形(如图2所示),又因为|a|=2|b|,所以a与b 的夹角为.故选B.
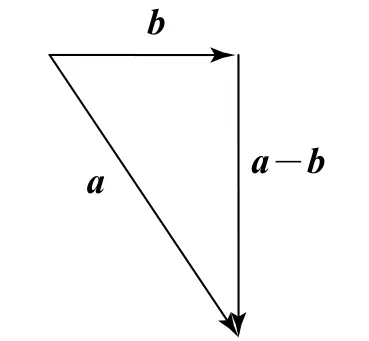
图2

本题也可采用常规解法,由(a-b)⊥b 可知(a-b)b=0,即ab-b2=0,则所以a 与b 的夹角为.这种方法虽然难度也不大,但结合图形进行计算更直观.

4 引入特殊数值,准确判断
A.a<c<b B.a<b<c
C.b<c<a D.c<a<b

综上,b>c>a,故选A.

求解数的大小比较问题,常规方法是构造相应函数,利用函数的单调性判断,或通过作差、作商进行比较.本题求解中通过引入特殊值,方法更为简捷.
5 把握极限位置,一望而答

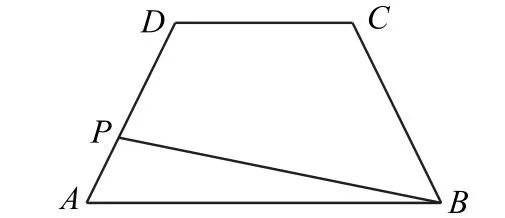
图3

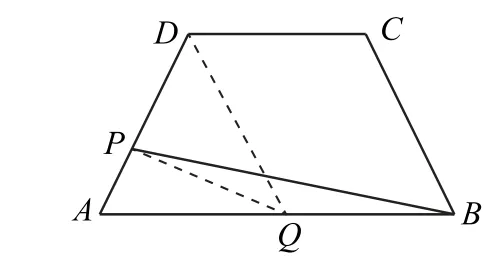
图4
由已知条件可知△ADQ 为等边三角形,所以当点P 与A 或D 重合时,即,取得最大值.当点P 为AD 的中点时取得最小值.所以的取值范围为[,8],故选C.

本题若采用常规方法,设
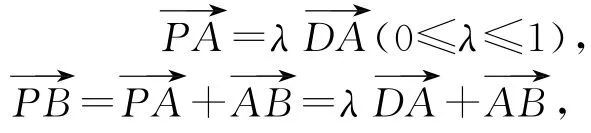
所以

如图5,过点D 作DE 垂直AB 于点E,由已知条件可得AE=2,AD=4,所以cos∠DAE=,所以
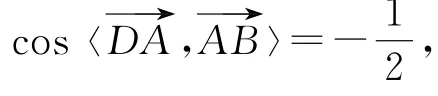
所以
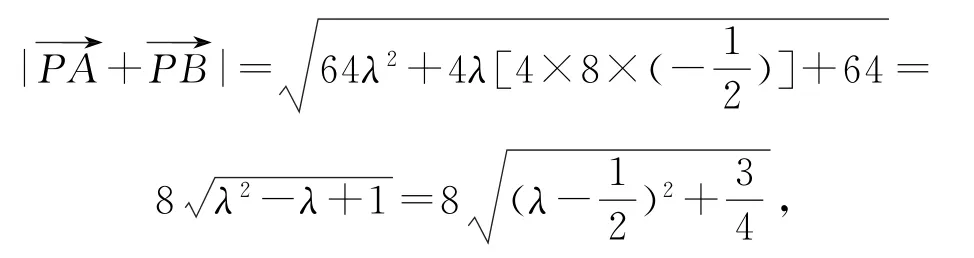
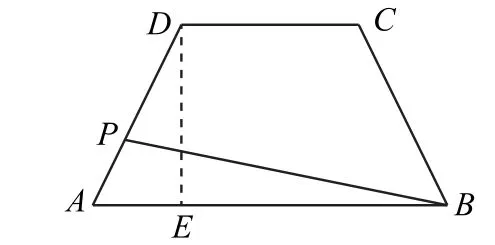
图5
当然也可以采用坐标法求解,此处略.
总之,对学生“多想少算”能力的培养,既是高考要求,也是教学要求.教师要在平时的教学中,有针对地进行这方面的训练,才能保证学生在考试中有目的性地先思考,再计算.

