初等行变换化矩阵为行最简形的方法与技巧

王炳涛

（山东交通学院威海校区基础教学部 山东·威海 264209）

0 引言

线性代数是大学数学中一门重要的公共基础课，在自然科学和社会科学领域有着广泛应用，其中的概念和思想方法是理工类和经管类专业学生的必备知识和重要数学工具。由于该课程教学课时少，教材内容抽象，题目运算量大，方法灵活多变，导致学生掌握程度偏低，在后续的专业课学习中不能学以致用。[1]

在线性代数中，矩阵的行最简形是对矩阵作初等行变换之后得到的一类特殊矩阵，它凸显了原有矩阵的核心性质[2]。利用初等行变换将矩阵化为行最简形是非常重要的方法，贯穿整个线性代数理论体系，可以说，只要能熟练掌握化行最简形的方法就能解决线性代数中大部分的计算问题。在教学过程中笔者发现，大部分学生能记住行最简形矩阵的特点，但是在利用初等行变换化行最简形时却非常吃力，步骤过多，正确率很低，究其原因主要是学生对一般的操作流程掌握不足，理解不充分，并且过多过早的使用分数，导致运算量大，出错率高。本文给出化矩阵为行最简形的一般流程，并提供一种避免出现分数的化简技巧，能大大提高学生化简的效率，降低出错率。

1 预备知识

1.1 行最简形矩阵的特点

行最简形矩阵具有以下三个特点：

（1）如果存在全零行，则全零行都位于矩阵非零行的下方；

（2）从上到下，各非零行的首非零元（从左边数第一个非零元素，也称为主元）左边零元素的个数在严格增多；

（3）各行首非零元都为1，并且这些首非零元1所在列其余元素都为零。

例如，以下矩阵都为行最简形矩阵：

如果矩阵只满足上述（1）（2）条，也称为行阶梯形矩阵。显然行最简形矩阵是特殊的行阶梯形矩阵，因此一般情况下要将矩阵化为行最简形就要先将其化为行阶梯形。行阶梯形矩阵的特点可简单描述为：从上到下，首非零元的列标在严格增大并且首非零元下方元素为零。从行最简形矩阵的特点我们知道，化成行阶梯形后还需要把各行首非零元上方元素化为零，最后把各行首非零元化为1即可。

1.2 矩阵的三种初等行变换

为便于读者理解，我们给出矩阵的三种初等行变换：

2 初等行变换化矩阵为行最简形的方法与技巧

2.1 初等行变换化矩阵为行最简形的基本步骤

根据以上分析，我们将初等行变换化矩阵为行最简形的步骤总结如下：

（1）用对换变换使得矩阵的全零行在非零行的下方，各非零行按照其首非零元的列标从小到大排序，首非零元列标相同的行相邻；

（2）从第一个非零行开始依次向下，将各行首非零元下方同列的元素用倍加变换化为0，变换过程中若出现全零行应换到非零行下方；

（3）从最后一个非零行开始依次向上，将各行首非零元上方同列的元素用倍加变换化为0；

（4）用倍乘变换把各非零行的首非零元化为1。

上述步骤可简单概括为“先把行排序，逆时针化零，主元同化一”。这个步骤与求解线性方程组的高斯消元法异曲同工，一定可以把矩阵化为行最简形，但是若严格用这个步骤化行最简形运算量较大，并非最优方法。

2.2 初等行变换化矩阵为行最简形的几点技巧

化行最简形的过程中要想减少运算量提高正确率，必须对步骤适当做出调整，具体如下：

第一，在利用首非零元将某些元素化零之前，可以先把首非零元化为1，这样就能避免在变换过程中出现分数或者过早的出现分数；

第二，将首非零元化为1后，在利用这个1将下方同列的元素化零时也可以同时把其上方同列的元素化零；

第三，在利用首非零元将下方同列的元素化零时可以不必先将首非零元化为1，而是借助最小公倍数，有时也很方便。

3 算例

本节通过给出四个具体算例来说明初等行变换化矩阵为行最简形的方法和技巧，首先给出一个一般情形下的算例。

然后根据前述变换原则执行以下步骤：

可以看到，例1在化简过程中前两行首非零元通过对换变换就能得到1，第三行首非零元通过简单的倍乘变换也容易得到1，但是还有很多矩阵的首非零元并不能轻易用对换变换和倍乘变换化为1，而要采用倍加变换才可以做到，我们给出下边的例子。

解：法一 先用对换变换将矩阵的行排序，原矩阵化为

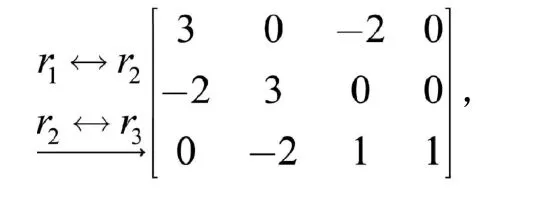
此时应先把第一行首非零元3用倍加变换化为1，步骤如下

然后用同样的思路把第二行首非零元9化为1，步骤如下

法二先化0后化1，从行排序后开始给出后续步骤[5]

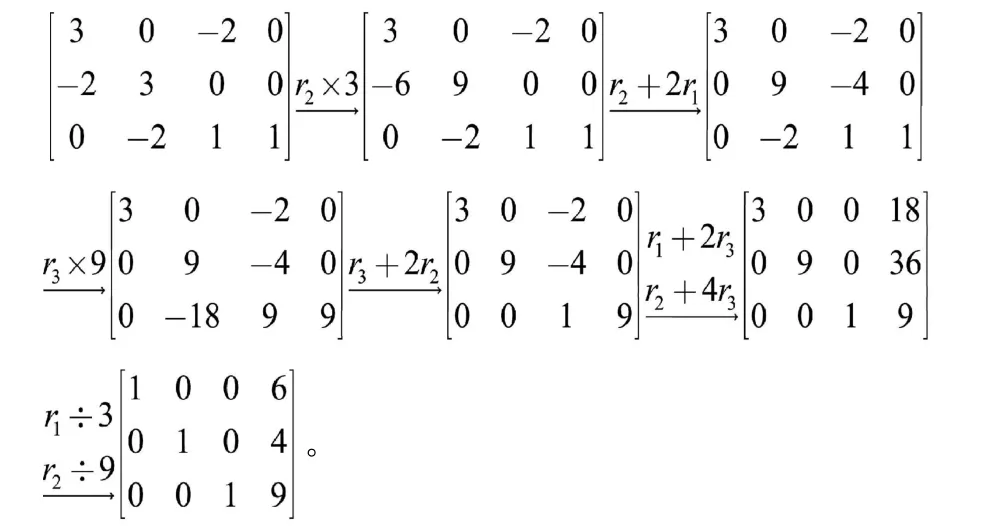
本例法一在将首非零元化为1时采用的是倍加变换，法二没有先将首非零元化为1，而是借助最小公倍数的思想利用首非零元把下方同列元素化为零，最后再把首非零元化为1，显然法一比法二更简便，也更容易掌握。下边给出常见情形的算例，进一步说明上述化行最简形矩阵的步骤和技巧。

本例在变换过程中，我们观察到第三步矩阵的第三行只要同除以2就能将首非零元化为1，这样做略微简单，但是有一定偶然性，不具有一般性，因此我们建议按照上述步骤来化最简形矩阵。

分析：本例容易观察到，第一列元素的最大公约数为25，利用第一行的首非零元25就很容易把下方同列元素化为0，因此第一步不需要把第一行首非零元化为1，事实上，如果先将其化为1，步骤就会很繁琐。

本题具体步骤省略，答案如下，仅供参考，

4 结束语

本文详细阐述了利用初等行变换将矩阵化为行最简形的具体方法和化简技巧，给出了几个典型例题来说明所述方法和技巧，希望能给学习该课程的高校学生和讲授该课程的教师一点启发和帮助。