时间分数阶Gardner方程新精确解的构建

黄 春

（四川职业技术学院教师教育系，四川遂宁629000）

非线性分数阶偏微分方程比整数阶偏微分方程更准确地描述现实中的物理现象, 并能够深刻反映物体内在性质. 非线性分数阶偏微分方程在控制理论、金融学、生物学、通信、化学等众多领域有着广泛的应用, 因此研究非线性分数阶偏微分方程的性质以及解的情况具有重要的意义. 构建非线性分数阶偏微分方程精确解的方法主要有: 首次积分法[1-2]、(G′/G)-展开法[3-4]、指数函数法[5-6]、Adomian 分解法[7-8]、Tanh函数展开法[9-10]等.

考虑如下时间分数阶Gardner方程[11-12]:

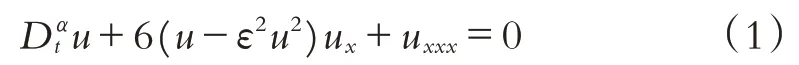
其 中: 0 ≤x≤1,t＞0, 0 ＜α≤1,是修正的Riemann-Liouville分数阶导数[13].

修正的Riemann-Liouville 分数阶导数由下式定义:

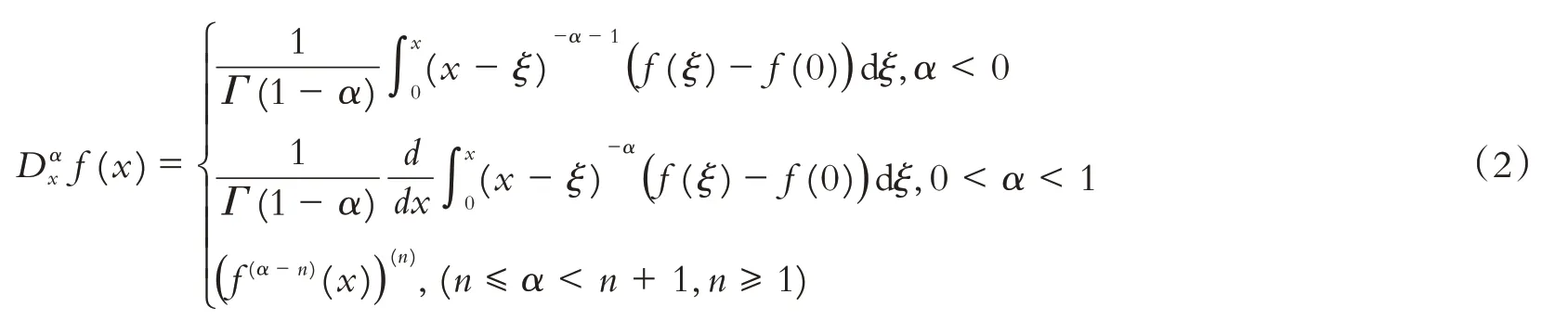
其中Γ(·)为Gamma函数,定义为:

修正的Riemann-Liouville 分数阶导数具有如下性质:

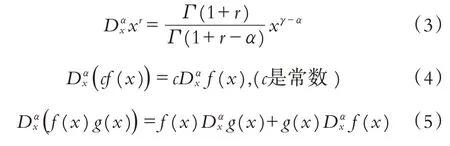
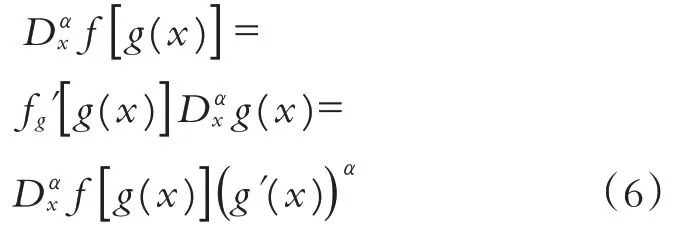
Gardner方程是一类重要的非线性模型,广泛应用于物理学领域的各个分支, 求其解长期以来为众多学者所关注. 整数阶Gardner 方程的精确解的求解方法有很多，如Painlevé 分析[14]、符号运算系统[15]、Darboux 变换法[16]、经典李群法[17]等, 但是对于时间分数阶Gardner方程精确解的研究却很少.Pandir等人[11]利用F-展开法获得方程（1）的Jacobi 椭圆函数解, Iyiola 等人[12]采用同伦分析法得到方程（1）的解析解. 本文拟用Riemann-Liouville 分数阶导数与修正的Tanh 函数展开法相结合，构建时间分数阶Gardner方程新精确解.

1 方法简述

考虑如下非线性分数阶偏微分方程：

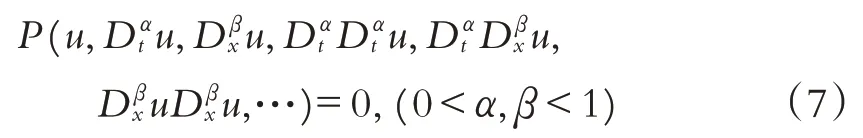
用修正的Tanh 函数展开法求解方程（7）的步骤包括3个步骤.

步骤1:作复变换

这里l,ω为常数.

在计算过程中需要使用导数链式法则：

将式（8）、（9）代入方程（7）中,方程（7）转化为只含变量ξ的非线性常微分方程：

步骤2: 假设常微分方程（10）的解可以表示为φ的多项式形式：

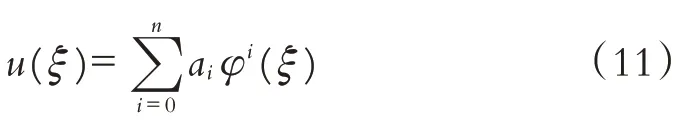
其中φ=φ(ξ)满足如下形式的Riccati方程:

这里的σ为任意常数,ai(i=0,1,2,…,n)为待定常数,正整数n可由齐次平衡原则确定.

对于φ, 根据常数σ的不同取值, 确定如下三种类型的解：

步骤3:将式（11）、（12）代入式（10）中,合并φ的同幂次项, 并令各次幂的系数为0, 得到关于ai(i=0,1,2,…,n)代数方程组, 计算参数代入（11）式, 得到方程（7）多个不同类型的精确解.

2 运用与结果

对方程（1）作复变换：

原方程转化为非线性常微分方程：

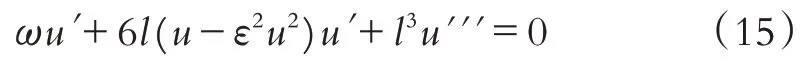
将方程（15）两边同时积分一次, 取积分常数为0可得：

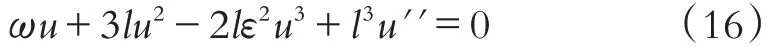
平衡最高阶导数项u3和非线性项u′′, 得n=1.因此式（11）为:

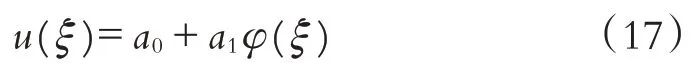
将式（12）、（17）代入式（16）, 合并φ的同幂次项并令其系数为0,得到关于a0,a1的代数方程组:

解上述代数方程组可得:

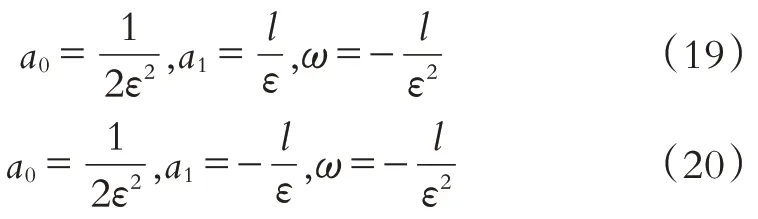
于是得到原方程在3种不同情形下的解.

情形1:当σ＜0时,方程（1）有如下孤立波解:

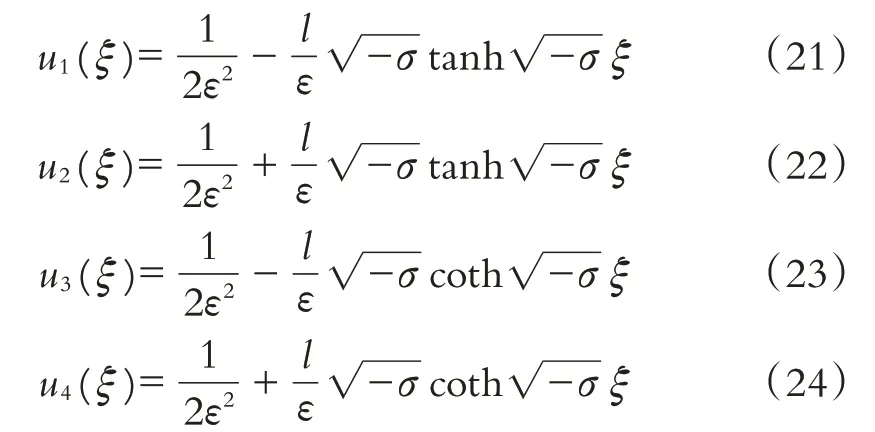
情形2:当σ＞0时,方程（1）有如下周期波解:

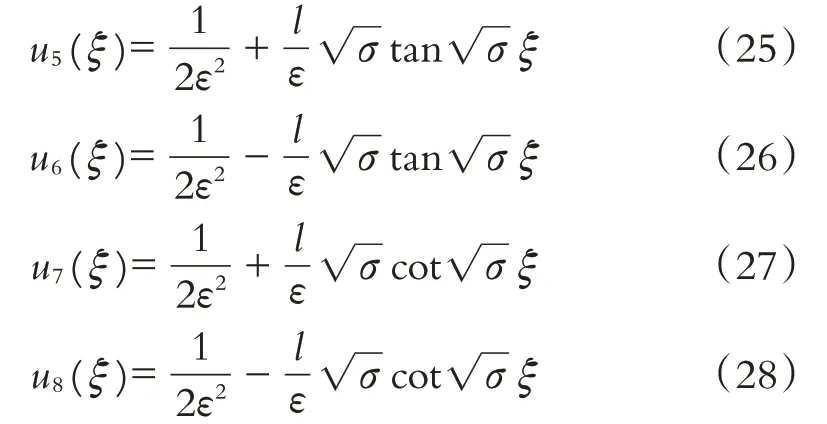
情形3:当σ=0时,方程（1）有如下有理函数解:

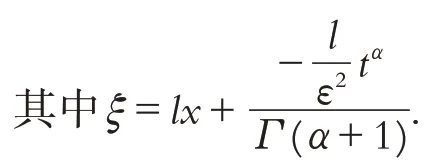
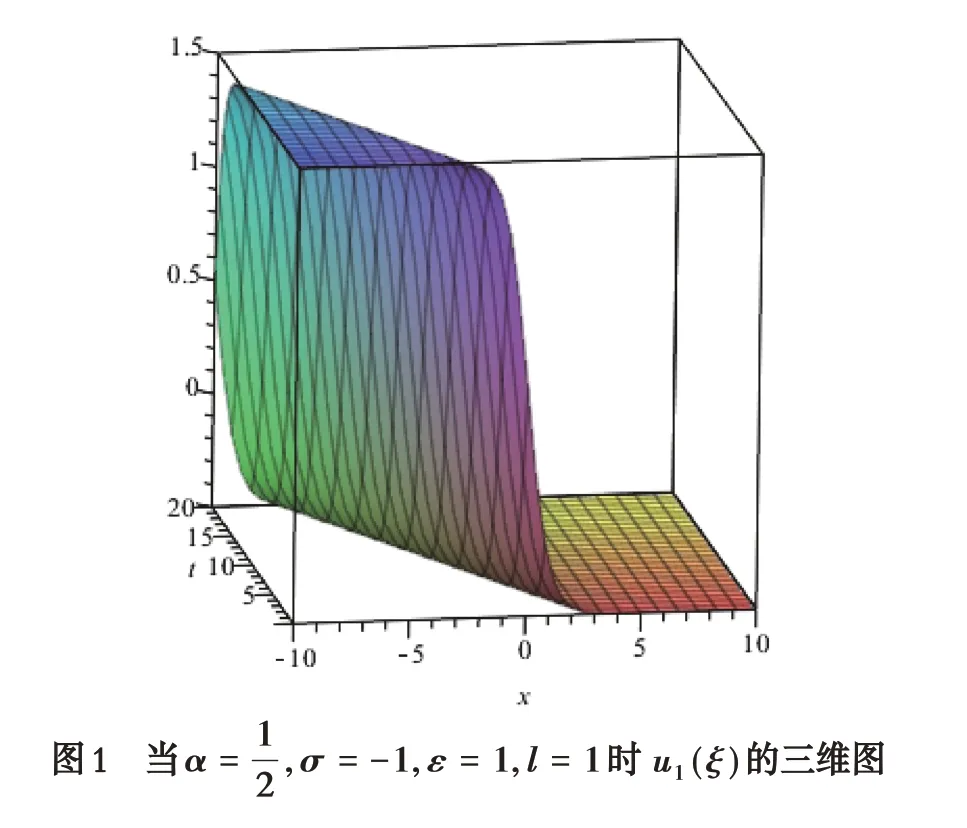
运用Maple 软件画出部分解的数值模拟图像如图1-3所示.

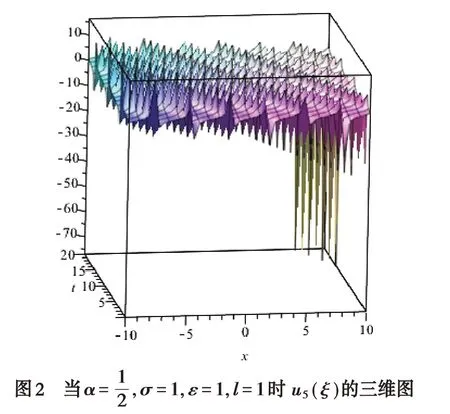
3 结语

本文借助Riemann-Liouville 分数阶导数结合修正的Tanh函数展开法构建时间分数阶Gardner方程的系列新精确解, 其中包括孤立波解、周期波解、有理函数解, 并对部分解作出三维图示. 这些解对于理解复杂的非线性物理现象并预测其发展趋势很有帮助, 该方法简洁高效, 是求解一般非线性分数阶微分方程行之有效的方法.