建筑工程质量组合评价模型的构建与仿真

肖光华，王清莲

（1.江苏城乡建设职业学院设备工程学院，江苏常州213147；2.河海大学计算机与信息工程学院，江苏南京210098；3.常州开放大学终身教育研究中心，江苏常州213001）

建筑工程质量是国家、社会和人民重点关注的重大民生问题之一，关系到广大人民群众自我安全感和幸福感，也关系到建筑企业的长远发展. 由于建筑工程的复杂性，影响其质量的因素很多，涉及设计招投标、施工组织管理、验收维护等诸多环节[1]，各环节的评价指标也不同，在现有的管理中，对工程质量评价往往依据实体质量的一部分作为质量好坏的评价标准，导致不同工程之间难以区分优劣，使得一些企业更愿意按照最低标准来建设，这对建筑行业的发展相当不利. 通过建立科学的工程质量评价体系，利用评价结果来区分工程质量的优良程度，可以让真正优质的工程脱颖而出，促进资源向优秀企业集中，倒逼评价不高的企业反思建设过程中存在的问题，从而促进工程质量的整体提高，最终形成良性循环，达到“良币”驱逐“劣币”的状态.

寻找一种准确、高效、量化的建筑工程质量评价方法成为学者们研究的课题. 李书全[2]等提出一种改进的SVM 模型用于施工项目安全预测评价；彭立新[3]等给出了特定的应用条件下的一种工程质量抽验方案；张敏[4]运用BP 神经网络算法来提高工程质量评价的精度；杨全[5]使用AHP-FUZZY 组合模型进行了实证探究；赵明华[6]等将相对熵的模糊评价群决策方法运用在工程质量风险控制中.

根据研究场景和样本的不同，SVM 和BP 神经网络算法有着各自的优缺点.SVM 对于非线性的小数据样本具有较好的泛化能力，但对大规模训练难以实施，对于多分类问题的解决有一定难度[7].BP神经网络也可实现非线性映射，有较好的自学能力和推广概括能力，但训练过程有可能进入局部最小值出现欠学习或过学习. AHP 作为一种主观赋权方法需要较大的专家样本，熵值法的客观性更强，但对于波动很小或者很大指标有一定的局限性. 综上所述，在现有研究的基础上，本文将层次分析法（AHP）和信息熵（Entropy）相结合设计了一套建筑工程质量的量化计算方法，并根据历史数据样本分别利用最优参数的支持向量机（SVM）和BP 神经网络进行检验评价，选择泛化能力最好的模型作为最终决策模型，并对该方法的可行性进行了验证.

1 评价模型的建立

首先根据已有成果和专家经验，采用层次分析法方法将人为的定性判断主观评价进行量化，确定主观权重；其次运用熵权法计算各指标对应的客观权重；最后将两者进行结合从而提供准确的量化指标.

1.1 基于AHP的计算模型

模型分为三层：目标层、准则层和决策层，通过分析各层之间的相互影响关系，构造目标层矩阵A和准则层矩阵Bi(i=1,2…n)，然后对同一层次的各元素与其所属的层次要素进行重要性的两两比较[8]，为了能将定性的判断进行量化，AHP 模型对所有结果通过9 个标度来计量，根据不同情况的评比给予数量尺度的评价[9].

用方根法将矩阵B的行向量元素的值相乘得到μij，根据每行元素数量n将结果开方，得到方根向量μi，将矩阵归一化后即为所求特征向量wi.即：

矩阵A的最大特征根λmax为：

式中(Aw)i表示向量的第i个分量.

计算一致性指标CI：

选取同阶数的一致性检验指标RI的值，求得一致性比率CR：

只有当CR≤0.1 时，可以认为判断矩阵的一致性是能够接受的.

准则层判断矩阵求解方法同目标层求解方法相同，求得特征向量wB最后，终得到AHP的主观权重：

由式（7）得出该层要素对于该要素的权重，然后由目标层及其隶属准则层得到的权重计算出主观权重.

1.2 基于信息熵的计算模型

相对于AHP 偏于主观的确定权重的分析方法，信息熵法是偏于客观的确定权重的方法，它借用信息论中熵的概念. 所谓“熵”，是信息论中衡量信息含量的量化指标，信息量的（概率）分布越趋于一致，其信息携带量就越大[10].

由评价方案中n个指标C1,C2,…,Cn，以及它们的m个客观属性组成决策矩阵D：

将决策矩阵D进行标准化处理得到决策矩阵R：

这里矩阵R中的元素rij满足归一性，即1(j=1,2,3,…,n).

指标属性Cj的熵Ej为：

式中：j=1,2,…,n；0≤Ej≤1.

若(r1j,…,rmj)=(0,…0,1,0,…)，则Ej=0；总之rij越一致，则Ej越接近1，这样就越不易区分方案的优劣.所以先计算熵值偏差度：

最终得到指标Cj的权重计算公式为：

1.3 基于联合赋权的计算模型

结合层次分析法和信息熵各自的优点，采用AHP 方法和信息熵联合赋权的方式评价工程质量，从而更好地反映工程质量的实际情况.由AHP计算求得的主观权重w′和熵值法计算求得的客观权重w′′，确定联合权重[11]：

1.4 基于SVM和BP神经网络的专家决策模型

SVM 作为一项数据挖掘的新技术，它以结构风险最小化为原则，通过核函数将非线性可分问题转化成线性可分问题，最终求得全局最优和唯一的解[12]. BP 算法由于其结构简单，可调整参数多，操作性好，获得了非常广泛的应用，它是前馈神经网络的核心，也是神经网络算法中应用最广泛的算法[13].样本数据的质量、数量以及数据训练的先后顺序都会对最终的预测精度产生一定影响，利用SVM 和BP网络各自的特点，选择泛化能力较好的模型作为最终的决策模型，具体实施步骤如下：

（1）将每个指标的评价度量值（1-10）作为模型的输入值，依据联合权重计算得到的评价结果作为模型的输出值，建立决策模型的学习样本集.

（2）将模型学习样本集分成两部分，随机抽取其中一部分的样本数据组作训练集，剩余的样本数据组作为检验集.

（3）将训练集数据和训练参数代入到SVM 和BP 网络模型中进行训练，通过迭代学习、训练结果评价和训练参数优化等一系列步骤，得到最终检验结果，选择预测结果中均方误差（MSE）较小，测定系数（R2）更接近于1的模型作为最终决策模型.

2 实验分析

评价建筑工程质量的好坏需要综合各方面因素的考量，为科学、全面地评价建筑工程质量等级，在查阅大量相关文献的基础上，结合江苏某建筑企业历年工程项目实施及验收数据，由该公司组成的专家组遴选了12 个质量因素指标，其模型结构及其相互关系如图1所示.

2.1 AHP主观权重计算

根据AHP 结构模型不同层次之间的关联关系，应用1-9 标度法量化目标层A、准则层B 以及决策层C的判断矩阵，由式（1）-（7）计算相应矩阵.表1-4分别为各层之间判断矩阵的特征向量wi值，表5为一致性检验相关参数，CR均小于0.1，则判断矩阵的一致性是能够接受的，各指标所占权重如表6所示.

图1 建筑工程质量评价体系

表1 目标层A和准则层B判断矩阵

表2 目标层B1和准则层C判断矩阵

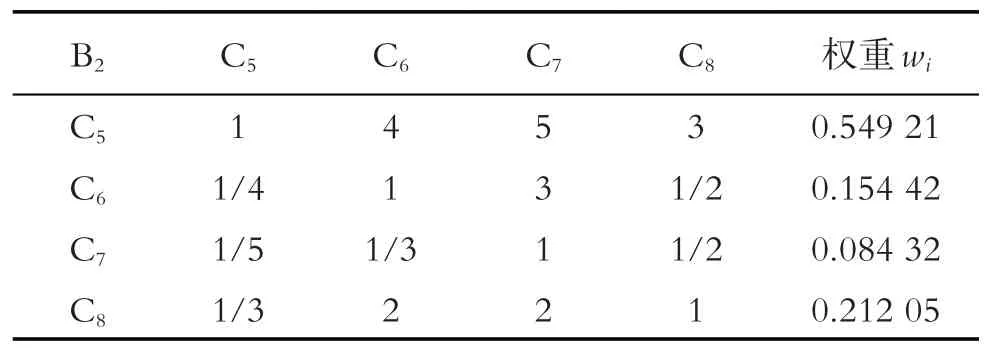
表3 目标层B2和准则层C判断矩阵

表4 目标层B3和准则层C判断矩阵

表5 参数值一致性验证

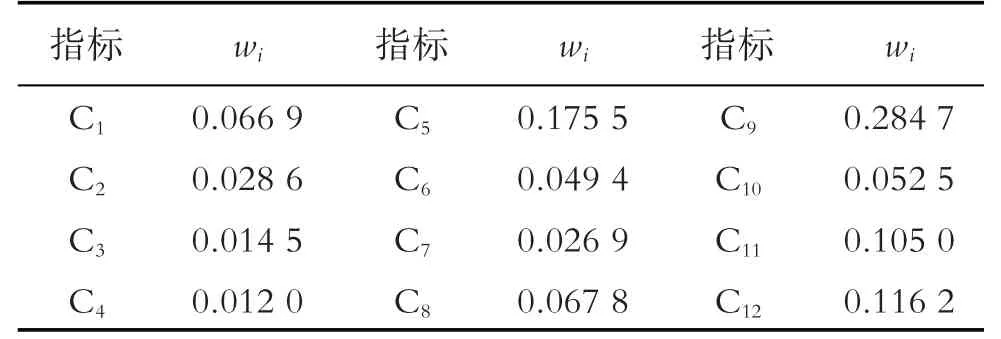
表6 AHP主观权重计算表

2.2 信息熵客观权重计算

信息熵是通过一个工程周期（从评估立项到交付使用再到后期维保）所付出的人力成本、购入固定资产折旧以及生产支出这三个维度来描述决策层的12 个指标，每个维度单位成本越高，则表明该指标对质量影响越大. 经无量纲处理后得到表7，由式（9）-（11）计算每项评价指标客观权重，如表8所示.

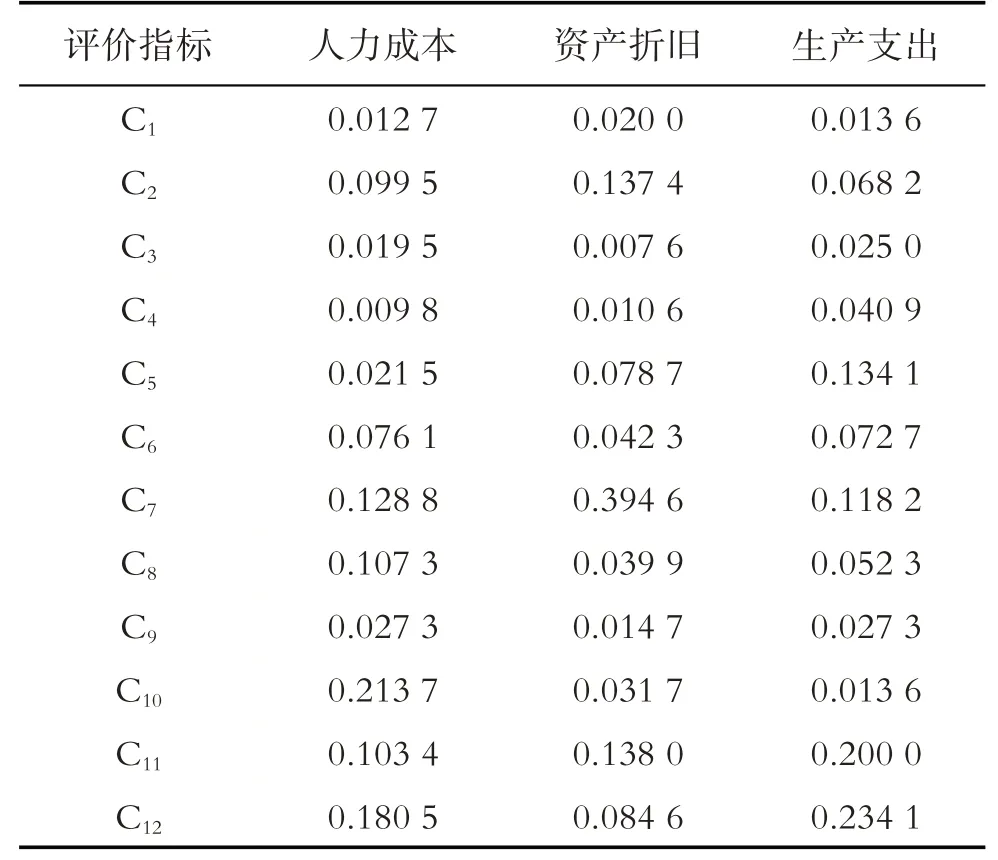
表7 信息熵决策矩阵

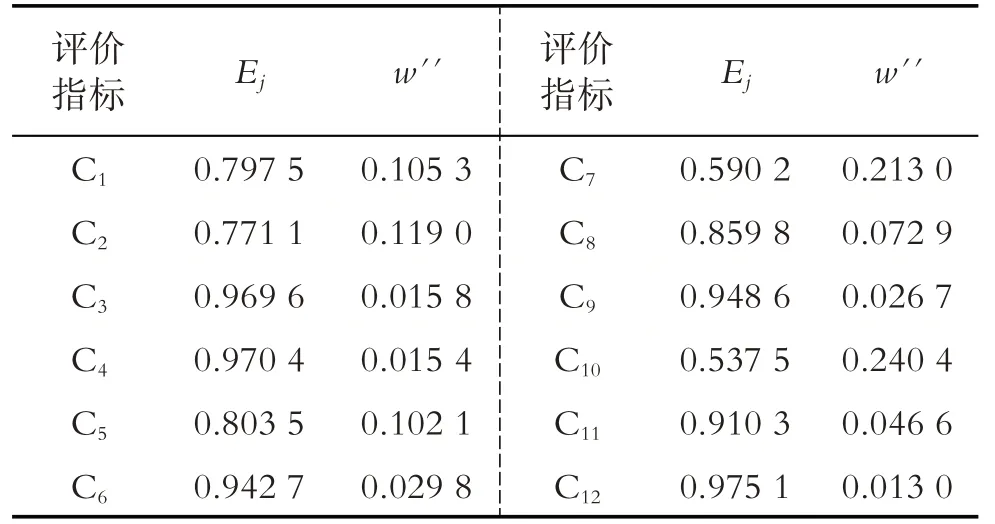
表8 信息熵客观权重表

2.3 联合评价指标权重计算

运用AHP 方法计算各层次特征向量并求得主观权重，运用熵值法求得决策层每项指标的客观权重，最终将主观权重w′与客观权重w′′按照式（12）计算得到联合评价指标权重w，如表9所示.

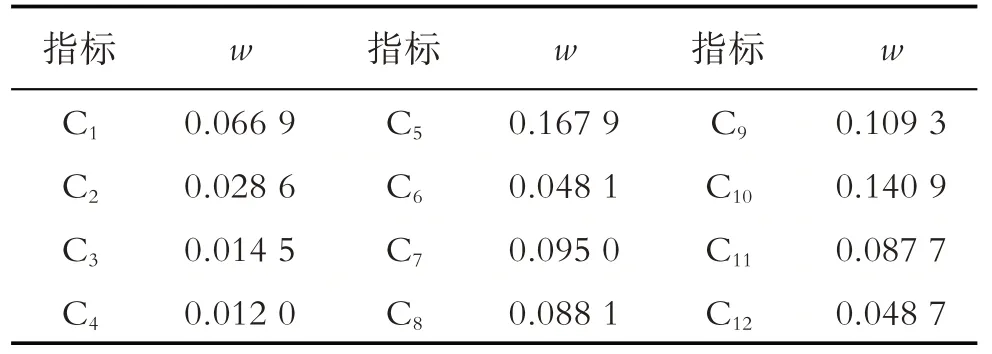
表9 联合评价指标权重

3 模型仿真

专家通过对指标进行赋分（1 ～10）计算出建筑工程质量的综合评价值，依据某建筑企业历史工程数据，专家组提供了60份样本数据.按照1.4节的步骤在MATLAB R2016a 下实施模型仿真，随机抽取50 份数据作为训练样本，剩余的10 份作为检验样本，然后进行模型精度的比较，选取最终决策模型.

3.1 SVM模型

经计算比较，选用径向基RBF 函数（Radial Basis Function）作为SVM 的核函数，通过交叉验证方法找到最优参数c（惩罚因子）和g（RBF 核函数的方差），得到c= 64，g= 0.0014. 其训练集的结果和检验集的结果比对如图2和图3所示.

图2 SVM训练集结果比对

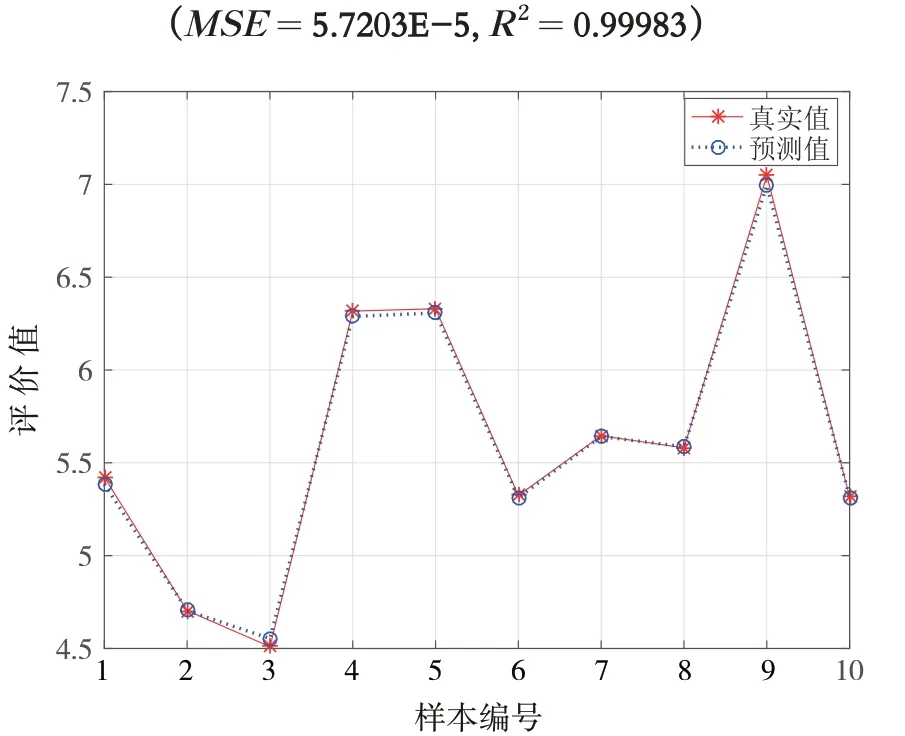
图3 SVM检验集结果比对（MSE=1.3248E-4,R2=0.99954）

3.2 BP神经网络模型

经参数优化，设置BP神经网络最多循环次数为1 000，目标误差小于0.001，学习率设定为为0.1，隐含神经元设为5，采用误差函数梯度下降法，其训练集结果和检验集结果比对如图4和图5所示.

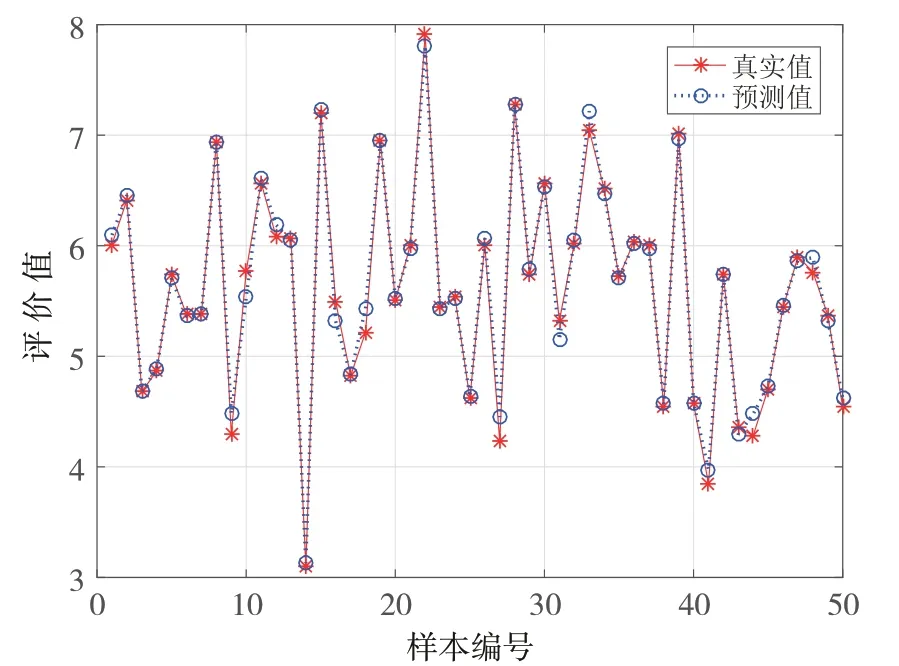
图4 BP神经网络训练集结果比对（MSE=1.4168E-3,R2=0.99184）

图5 BP神经网络检验集结果比对（MSE=4.0809E-3,R2=0.96277）

3.3 结果比较

通过计算两种模型均方误差MSE和决定系数R2，由表10 可知，两种模型都具有良好的泛化能力，测试结果误差也都在可接受的限度内，而SVM 检验效果更优. 将训练好的模型进行保存，当再进行同类工程质量评价时，只要输入待评价指标数据，启动训练好的模型，就可以得到工程质量的综合评价值.

表10 两种模型检验集精度对比

4 结语

本文针对建筑工程质量评价中存在的问题，提出了一套新的评价指标量化方法，将AHP 方法和信息熵相结合，从主、客观角度量化对比建筑工程质量的优劣程度. 采用SVM 和BP 神经网络构建建筑工程质量的评价模型，经实验证明，评价指标计算方法合理，模型检验精度令人满意，对形成建筑工程质量评价大数据大有裨益，从而能促进建筑企业的良性发展. 当然，建筑工程质量的评价是一个非常复杂的非线性问题，本文只是初步的探索，对于样本数据的获得，样本数据对模型泛化能力的影响以及模型算法的改进是未来需要更深入研究和探讨的.