层叠式磁力调频压电电磁复合能量收集器设计
王宪菊,陈 韬
(阜阳师范大学物理与电子工程学院,安徽阜阳236037)
随着电子技术的飞速发展,便携式电子产品、MEMS微机电系统和无线传感网络在军事、医疗、民用和工业生产中得到广泛应用[1],但大多数微电子设备供电能源仍依赖于化学电池,而化学电池存在能量密度小、需定期充电或更换以及环境污染等问题,无法满足微电子设备高速发展的需求. 环境中的振动能在日常生活和工程现场中广泛存在,且不受天气、位置等因素影响,越来越多的专家和学者致力于研究将环境中的振动能转换为电能,为微电子产品就近提供电能[1],因此俘获环境中的能源实现微电子产品能量自给成为一种很有前景的技术[2].通常学者们研究的压电电磁复合能量收集器以线性系统为基础,工作频带窄,谐振频率固定,无法与环境中振动频率匹配,导致俘能效率低[3]. 本文在复合俘能器研究的基础上,建立调频俘能器机电耦合数学模型并对其进行分析,利用MATLAB 进行理论仿真. 制作层叠式压电电磁复合能量收集器样机,通过改变磁距可调节俘能器的谐振频率,使其与振源频率匹配,提高了俘能效率和输出功率,实验结果与仿真结果高度吻合,为实际工程应用提供了理论和实验依据.
1 磁力调频压电电磁复合俘能器结构设计和工作原理
图1 为层叠式磁力调频压电电磁复合能量收集器的结构简图. 能量收集器由FR4 板、质量块磁铁、调频磁铁、固定弹簧和感应线圈组成. 本结构采用三层亚克力板,上中两个亚克力板组成电磁层,上中下三层板组成压电层. 其中上层板、中间板和下层板由4 根支柱贯穿,弹簧套入支柱,实现能量传递.压电层的上层亚克力板固定质量块磁铁,中下层亚克力板上固定有调频磁铁,极性相反,其间的吸引力使系统引入非线性刚度[4],因此,改变两个磁铁之间的初始距离可以调节能量收集器的谐振频率. 对系统沿Z 方向施加激励时,压电陶瓷片工作在d33模式,将机械能转换为电能. 质量块磁铁与感应线圈之间的相对运动产生感应电动势.

图1 磁力调频压电电磁复合能量收集器结构简图
三层亚克力板分别夹持半径为rp,厚度为hp的圆形压电陶瓷片,中下层亚克力板上的两个相对陶瓷片受力方向相同,电学上与线圈并联连接,输出端通过整流桥接负载电阻R,质量块磁铁与调频磁铁尺寸相同,半径为rc,高为hc,调频磁铁初始距离为d0,线圈高为hx,内外半径分别为Ri、Ro.
2 磁力调频复合俘能器发电特性的数学模型分析及MATLAB 仿真
2.1 数学模型分析
磁力调频复合能量收集器机电耦合数学模型如图2所示.
首先分析电磁机电耦合系数及输出功率,单个电磁俘能器是基于电磁感应定律,线圈内感应电动

图2 复合能量收集器机电耦合数学模型
势与穿过线圈磁通变化率有关[5],即:

式中:N为线圈匝数,Φ 为通过线圈的磁通量,θe为电磁机电耦合系数,z˙为磁通相对线圈的运动速度.
单个线圈输出功率可表示为:

然后分析单个压电振子机电耦合模型,压电振动能量收集器是一个谐振器件,由振动理论可知,单自由度能量收集器可以等效为一个质量——弹簧模型[6]. 当某一时刻系统发生振动,模型相对于外界发生的位移为yn(t),磁铁质量块相对于模型发生的位移为zn(t),压电耦合系数为θn,根据牛顿第二定律,列出机电耦合方程:
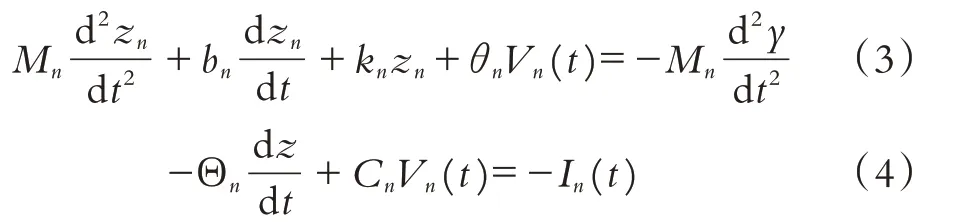
因此,压电能量收集器总的输出功率为上下两个压电振子的输出功率之和,瞬时功率可以表示为:

在压电俘能器、电磁俘能器基础上耦合磁力作用即得磁力调频压电电磁复合能量收集器模型,根据公式(1)-(4),可得该模型的机电耦合方程:
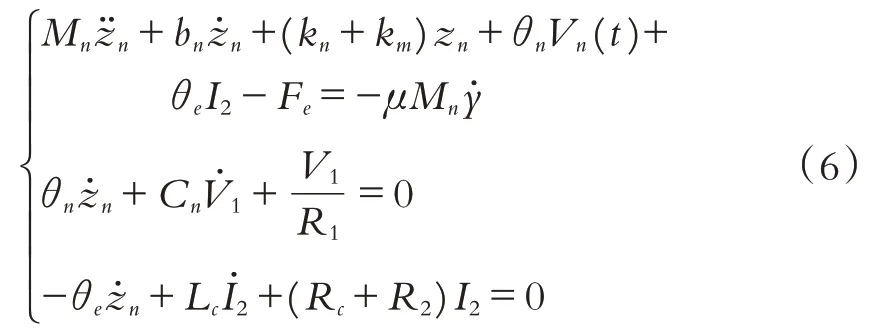
(1)系统谐振频率. 采用简单的Willians-Yates模型,运动微分方程通过振动y(t)=Y0coswt和磁铁质量块的相对位移z(t)对系统加以描述[7],运动微分方程如下:

在这种模型下系统的谐振频率为:

考虑到压电、电磁机电耦合以及磁力作用,系统的等效刚度为:
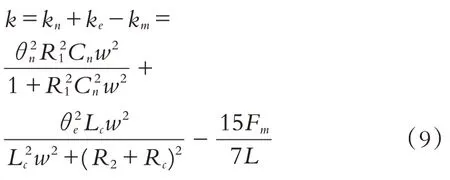
(2)系统能量转换效率. 能量转换效率是评估能量收集器发电性能的一项重要指标. 当系统受到外部激励时,经过一个周期,外部机械能转化为两部分能量:一部分由于存在机械阻尼而变成热能散耗掉,一部分是电阻上的电能[8]. 转换效率为平均功率的比值,即:

激振力和压电振子的位移分别定义F=M1Agsinwt,y=ymsinwt. 其中,Ag为激励加速度的幅值,ym为位移的幅值[9].
系统的输入功率为:
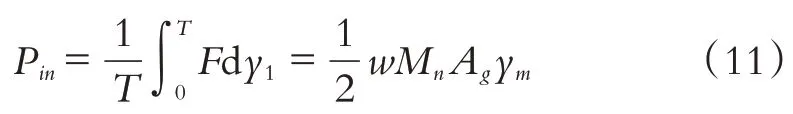
磁力调频压电电磁复合能量收集器的转换效率为:
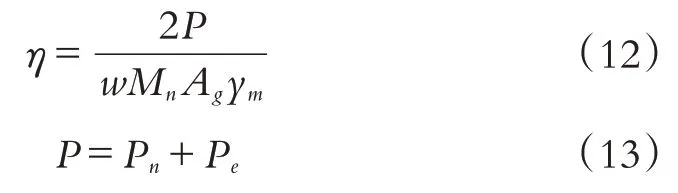
由理论公式可见,能量收集器的发电特性主要受系统的等效质量M1、等效刚度K1、频率ω、机电耦合系数θn和θ e、负载电阻R1和R2的影响. 由于等效质量M1在实际应用中不易改变[10],由公式(8)和(9)可知,机电耦合系数θn和θe、负载电阻R1和R2和频率ω的改变均能改变俘能器的等效刚度. 因此本文主要研究等效刚度对俘能器发电性能的影响,而等效刚度的改变依赖于调频磁铁的磁力大小[11-12],手动调节磁矩即可改变磁力.
2.2 MATLAB仿真
利用MATLAB 对数学模型进行仿真,分析俘能器在简谐激励下等效刚度对其发电性能的影响. 图3 为改变磁矩得到的俘能器输出功率频率响应. 随初始磁矩减小,吸引力增强,系统刚度减小,谐振频率减小,输出功率峰值左移.

图3 输出功率频率响应曲线(理论结果)
3 调频压电电磁复合能量收集器发电特性实验
由数学模型分析可知,通过改变调频磁铁距离可以调节俘能器的谐振频率,使其与激振频率相匹配,从而使发电性能达到最优.
按照表1 的结构参数研制实验样机,搭建实验平台,测量俘能器的输出功率频率响应,并与理论结果进行对比分析,验证理论模型的正确性.

表1 制作材料
3.1 样机制作及实验测试平台搭建
层叠结构的磁力调频压电电磁复合俘能器实验样机由三层亚克力板组成,中下层亚克力板上均夹持9 个压电陶瓷片,每个压电陶瓷片中心固定一个调频磁铁,中间层亚克力板固定9个线圈.当样机振动时,磁铁与线圈产生相对运动,线圈内部感应电流;同时压电片受压变形,电极表面产生电荷. 样机如图4所示.
振动信号由振动台提供,在振动俘能过程中,俘能器外接负载电阻R1和R2,采用安捷伦示波器观察电阻两端电压.
3.2 磁力调频俘能器最优匹配电阻
(1)压电振子最优电阻匹配. 上下磁铁端面距离设定为30 mm.线圈两端导线断开,仅改变压电振子两端的负载电阻,每次改变1 kΩ,最终确定磁力耦合结构下复合俘能器压电部分的最优负载电阻为55 kΩ.
(2)线圈最优电阻匹配. 固定压电振子外接负载55 kΩ,改变线圈外接负载电阻,每次改变量为500 Ω,实验发现,当电阻值在(3.5 ~4.5)kΩ时,复合俘能器输出功率出现波动,但振动幅度很小,不足3.7 mW 的1%. 考虑到测量仪器精度,振动台输出力精度等限制,最终确定电磁线圈的外接负载保持在4 kΩ.

图4 样机
3.3 磁矩对复合俘能器输出功率的影响
图5 为层叠式磁力调频压电电磁复合俘能器在不同初始极距时的输出功率频率响应. 初试极距为30 mm 时匹配负载电阻,且保持不变. 对照图4,减小初试极距,俘能器的谐振频率均减小,说明实验结果与理论吻合. 当初试极距为25 mm 时,层叠式磁力调频压电电磁复合俘能器的峰值输出功率为3.2 mW,在相同振动频率下,初试极距为30 mm 时输出功率约为0.65 mW,峰值输出功率提高了约4 倍. 因此,实验结果再次证明可以通过改变调频磁铁初试距离的方式调节复合俘能器的谐振频率,从而提高俘能器的峰值输出功率,增强其环境适应能力.
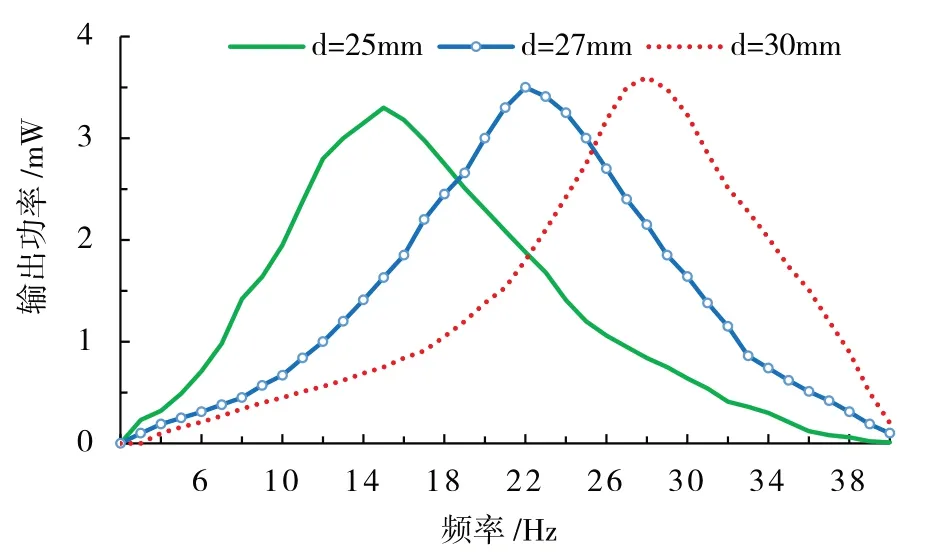
图5 输出功率频率响应曲线(实验结果)
4 结语
本文研制了一种层叠式磁力调频压电电磁复合俘能器,搭建了实验测试平台,对俘能器的输出功率频率响应进行了实验测试. 实验结果与理论结果比较接近,验证了数学模型的正确性和磁力模型的有效性.

