注重过程 激活思维 提升素养程利梅

程利梅

“数学是思维的体操”.《新课程标准》对思维能力的发展这样阐述：能力的发展绝不等同于知识和技能的获得.能力的形成是一个缓慢的过程，有其自身的特点和规律，它不是学生“懂”了，也不是学生“会”了，而是学生自己“悟”出了道理、规律和思考方法等.这种“悟”只有在数学活动中才能得以进行.因而教学活动必须给学生提供探索交流的空间，组织、引导学生“经历观察、实验、猜想、证明”等数学活动过程，并把能力的培养有机地融合在这样的“过程”之中.

数学课程的内容为数学结果形成的过程和数学思想.数学结果形成的过程是数学课程内容的一部分，学生也只有经历了数学活动，思维才能得以发展.所以，我在教学中注重让学生经历数学结果形成的过程，使学生的思维始终处于运行中，以此來激发学生的学习兴趣，培养学生的思维能力，提高学生的数学素养.下面我以“三角形内角和定理的证明”为例来阐述我的观点.

本节课是人教版八年级上册第11章《三角形》第二节《与三角形有关的角》第一课时《三角形的内角》中的内容.在教这部分内容时，教师的做法可以总结为两种：（1）动手测量、折叠、拼凑，这些方法属于实验几何;（2）作辅助线通过推理论证得到，这属于论证几何.观察、实验是发现数学公式、定理的重要途径，而证明则是确认数学公式、定理的必要步骤.这种从实验几何到论证几何的理性过渡，就是数学理性精神的落实.实验几何可以激发学生的学习兴趣，而论证几何则可以培养学生的推理能力.

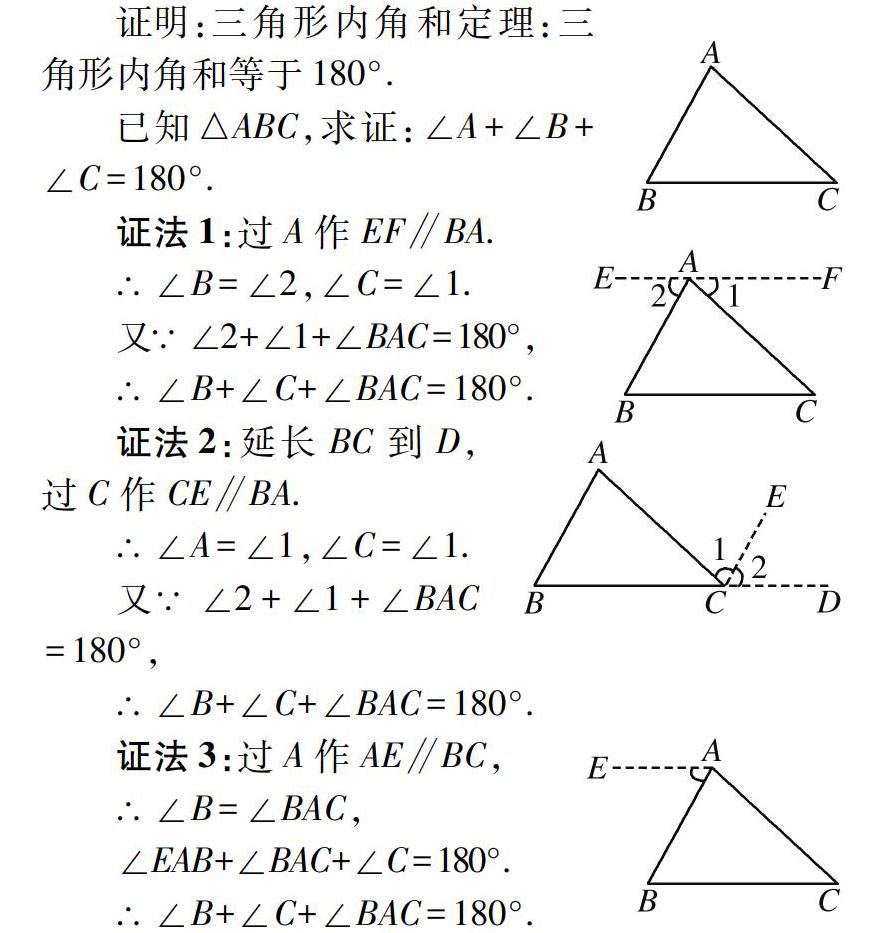
在证明定理时，作辅助线其实有很多种方法，我们可以过三角形的顶点处作辅助线，也可以过三角形一边上任意一点作，这一点可以是在三角形内部的一点，也可以是三角形外部的一点，也就是说这一点可以是平面内任意一点.

无论我们过哪一点作辅助线通过推理论证，都可以让学生“懂”了，让学生“会”了.我的问题是，这样的教学设计，学生自己“悟”出了这样做的道理吗？学生自己“悟”出了思考方法吗？或者如果有学生问：怎样才能想到作这样的辅助线呢？这才是学生在学习新知时思维卡壳的地方.他找不到新旧知识的连接点.苏霍姆林斯基在《给教师的建议》第12条“关于获取知识”中，有这样一句话“进行教学，要靠已有的知识来获取新的知识——这在我看来，就是教师水平高的表现.”

学生在本章仍处于进一步熟悉证明的阶段，学习通过推理的方法证明“三角形内角和等于180°”有一定的难度.我进行了如下教学设计：想一想，我们在哪里学到了180°？在人教版七年级上册第四章“几何初步”学“角”的时候出现过平角等于180°.还有在人教版七年级下册第五章“相交线与平行线”部分学平行线三线八角时出现过180°：两直线平行，同旁内角互补，互补就是180°.这样学生就有了思考方向，构造平角或者同旁内角.即将三角形的三个内角转化为一个平角，或转化为一对同旁内角.这样学生就清楚了，为什么要这样作辅助线，怎么才能想到这样作辅助线.我们知道，学生已有的经验和知识是学生理解数学的基础.“三角形内角和定理的证明”对于学生来说是一个新的问题，把这个新的问题转化为已经知道的“平角或同旁内角”知识来解决.这就是数学的转化思想.我在本节课的教学设计中注重让学生经历探究辅助线产生的过程，激发学生的学习兴趣，培养学生的思维能力，提高学生的数学素养.

毕达哥拉斯：在数学的天地里，重要的不是我们知道什么，而是我们怎么知道.让学生在动手画、动脑想、动口说中，经历数学知识形成的过程，才能真正地让学生体验我们“怎么知道”.