以形促思 演绎算理
陈娟

[摘要]關于两位数乘法计算,学生大多数只掌握了算法,却对算理知之甚少,这在很大程度影响了学生对乘法的运用和掌握。为此,在教学中可运用数形结合思想,借助直观的图形演示,促进学生思考,让学生经历数学化的过程,进而掌握算理并将其逐步内化成算法。
[关键词]数形结合;乘法计算;算理;算法
[中图分类号]G623.5 [文献标识码]A [文章编号]1007-9068(2020)14-0069-02
《课程标准解读》中指出:义务教育阶段,许多重要的数学内容、概念都具有“数”和“形”两方面的本质特征,即数形结合是认识数学的基本角度,与其说是方法,不如说是基本要求。
最近笔者听了“有趣的乘法计算”一课,该课是苏教版教材三年级下册第18、19页的内容,包括两位数乘11的算法、“首同尾合十”的算法、(a+1)×(a-1)=a×a-1的算法,从课堂反馈来看学生对每一种算法的理解都不是很透彻。而笔者在六年级的数学课堂上也出示过这三类问题,发现只有少数学生对两位数乘11的算法还有一点印象,而对其他两种算法则完全不记得了,更别提运用了。结合六年级学生的现状,反思所听的课,笔者以为对于算理的透彻理解要摆在首位,只有在理解算理的基础上,学生对算法的印象才会深刻,才能从记忆走向运用。下面,笔者从理解算理的角度谈一谈对于“有趣的乘法计算”教学的调整与反思。
【案例描述】
教学片段一:两位数乘11的算法
(1)列竖式计算下面一组算式,你有什么发现?
16×11 43×11 78×11 96×11 24×11
让学生用竖式计算并核对答案后思考:积的每一位上的数和原来的两位数相比,你有什么发现?先自己想想,再和同桌说说。
(2)汇报交流:积的个位是__;积的十位是__;积的百位是__。
引导学生总结:积的个位是原来两位数个位上的数;积的百位是原来两位数十位上的数;积的十位是原来两位数个位和十位上的数的和。
(3)猜一猜53×11的积,你是怎样想的?
根据上面总结的规律,猜想53×11=583,并用竖式验证,发现猜想正确,进一步总结规律,简化为“两头一拉,中间相加”。
(4)猜一猜64×11的积,说说想法。
师:你觉得64x11=6104的算法对吗?
生1:不对,因为两位数乘两位数,不可能得到四位数。(此错误教师和学生均没有发现)
生2:我是估算的,64接近60,11接近10,它们的积会比600大一些.但6104太大了。
师:这里的计算过程和前面有什么不同?
生3:十位上满十要进一。
(学生列竖式计算,得到结果为704)
师:这里百位上的6为什么变成了7,多出的1从哪里来的?
(完善算法:两头一拉,中间相加,十位满十,百位加一)
教学片段二:探索“首同尾合十”的算法
出示:22×28 47×43 41×49 56×54 62×18
师:观察每个算式中的两个乘数,你发现了什么?
生1:两个乘数十位上的数相同。
生2:个位上的数相加等于10。
师:像这样的算式,叫首同尾合十算式。
师(出示上面算式的得数):积和原来的两位数相比,你有什么发现?其中究竟藏着怎样的秘密呢?积的末两位是怎么算出来的?积的末两位前面的数呢?
师:当两个两位数相乘,十位上的数相同,个位上的数之和为10时,积的末两位等于两个乘数个位上的数相乘的积,积的末两位前面的数等于原来乘数十位上的数与比它大1的数的乘积。
猜答案:35×35 45×45 25×25 15x15 55×55
教学片段三:探索(a+1)×(a-1)=a×a-1的算法
出示:64×66 74×76 84×86
师:运用“首同尾合十”的算法迅速填写结果,然后再说说是如何快速而准确地完成的。
师:当两个两位数相乘,十位上的数相同,个位上的数相差2时,乘积为两个乘数的平均数的平方与1的差。
【案例反思】
同一节课的三个教学片段,都是以“计算多个同类型题,观察结果,发现计算规律”为主线贯穿全课教学。学生并不能经过自主交流进而发现计算的规律,片段一中虽然有一小部分学生在教师的引导下能够发现规律,但却出现一个错误的想法:两位数乘两位数,不可能等于四位数;存在一个疑问:对于64×11=6104,为什么学生在竖式中会把十位进的1和百位的6相加,而在口算中却会出现错误?而片段二和片段三的学习内容难度较大,学生很难发现其中的规律,全部由教师来总结。究其原因,主要还是学生只掌握了两位数乘法计算的算法,却对算理知之甚少。
那么,如何帮助学生理解算理呢?一方面可根据学生的年龄特征将本课分解成两个课时,另一方面,运用数形结合思想,借助直观的图形演示,促进学生思考,同时抓住知识的生长点,让学生经历数学化的过程,用清晰、具体的实物操作来演绎算理,再逐步将算理内化成算法。
1.数形结合,遵循儿童认知规律
皮亚杰的认知发展理论指出:具体运算阶段是指七到十一岁的儿童的认知发展阶段。这一阶段,儿童能根据逻辑法则进行推理,但这种思维能力仅局限于具体情境或熟悉的经验。举个例子:如果问一个三年级的学生“A>B,C
2.数形结合,具象表征演示算理
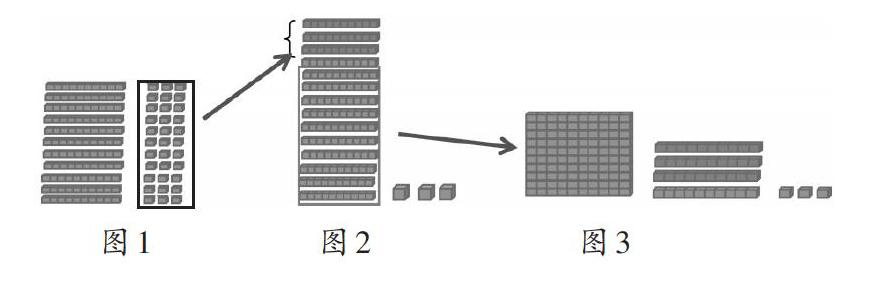
以13×11为例,从乘法的意义上理解,它就是11个13相加的和,以小正方体来演示(如图1),单个单个的小正方体有11个3块,其中有10个3块可以拼成3个十,再把这3个十和原有的11个十相加(如图2),其中10个十满100可以拼成1板,也就一个百,即向百位进一,此时十位上还有剩下的1个十和个位进上来的3个十,所以十位上是4个十(如图3)。以此过程来演绎“两头一拉,中间相加”的算法,既直观又形象。
以具体的图形摆一摆、圈一圈的形式,使学生能够自主总结抽象出“两头一拉,中间相加”的算理。此时再结合竖式来观察结果,则算理和算法的关系自然打通。
3.数形结合,演绎推理深度思考
波利亚很早就注意到“数学有两个侧面……用欧几里得方式提出来的数学是一门系统的演绎科学;但在创造过程中的数学却是实验性的归纳科学。”因此,与之对应的应该有两类推理:用合情推理获得猜想,发现结论;用演绎推理验证猜想,证明结论。上述三个教学片段中,教师都试图引导学生计算,比较不同的算式,总结计算规律,让学生经历了一个合情推理的过程。但学生难免疑惑:这一类型的计算都有这样的规律吗?有没有不一样的?此时,需要一个由具体数值计算到符号公式表达的过程。小学阶段,学生只是初步接触演绎推理,只能借助图形让其感知计算规律的一般性。
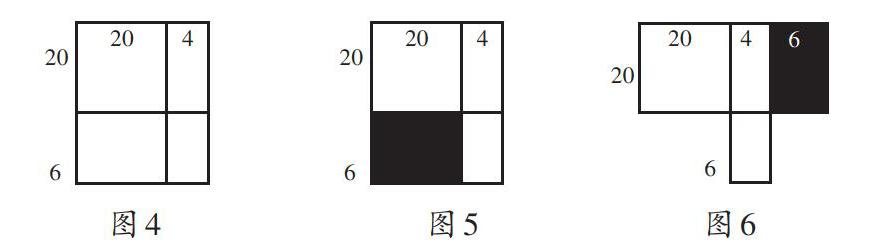
例如,探索“首同尾合十”算法和(a+1)×(a-1)=a×a-1的计算规律时(以26×24为例),可进行如下处理:大长方形面积为26×24(如图4),可以看作是20~20的一个正方形和三个小长方形的面积的和,通过把图5中面积为6×20的小长方形移动到图6中对应的位置,可得大长方形面积为20×(20+4+6)+4×6,即20×30+4×6。通过图形可知“首同”即为正方形边长的整十数,无论几十都可以;“尾合十”,可以把图上的4+6换成3+7、2+8、1+9、5+5,验证可得总结出来的规律都是适用的。
美国数学家斯蒂恩说:“如果一个特定的问题可以被转化为一个图形,那么就整体地把握了问题,并能创造性地思索问题的解法。”以形促思,演绎算理,让学生经历数学化过程,可有效夯实其对算理、算法的掌握,提高数学教学效率。
(责编:罗艳)

