“确定位置”的内涵、要求和数学化教学路径

丁洪

[摘要]解读确定位置专题知识的内涵和教学要求，提出确定位置的数学化教学路径，即横向数学化与纵向数学化结伴而行，并凸显情景的服务、过程的完整、方法的对比和思想的渗透，以有序建构物体的位置模型，有效发展学生的空间观念。

[关键词]确定位置;内涵;要求;数学化;教学路径

[中图分类号]G623.5 [文献标识码]A [文章编号]1007-9068（2020）14-0004-03

确定位置属于“图形与几何”板块，主要学习“运用坐标描述图形的位置”。教学时，必须思考和解决“为什么要确定位置？怎样确定位置？用什么方式引导学生建构确定位置的方法？不同确定位置模型之间有什么联系和区别？”“不同学段的内容安排和要求侧重是什么？”“确定位置教学的增值点在哪里？”等问题。只有把这些问题弄清楚、想通透，才不至于囿于一隅、安于一课，也才能避免“教得了”却“带不走”的尴尬。

一、“确定位置”的内涵解读

1.生活中的确定位置

人们一直在探索和认识世界，试图精准记录物体的位置，使其更好地服务社会生活。一是地物定位，主要依靠大地上的特殊标志物，如高山、河流、峡谷和灯塔等，确定方法原始，确定范围较小，而且误差较大。二是天文定位，主要利用宇宙中的日月星辰，如夜空中的北极星定位，确定方法相对科学，确定范围变大，但极易受到自然条件限制。三是工具定位，像指南针、六分仪、精确计时仪等，是简单工具的使用;像无线电、卫星导航、综合卫星导航等，属于现代工具，能精准定位海、陆、空中的任意对象，基本实现“无死角、全覆盖”。显然，生活中的确定位置源于实际需要，是人类探究、刻画和记录世界的产物。

2.数学中的确定位置

数学中的确定位置属于规定性知识，其本质属性是人的发明创造。确定位置一般遵循两个创造原则，一是刻画对象的数要尽量简单，做到参照物的选择与具体情景需求统一;二是描述方式要简约明了，做到数学约定与实际表达内在吻合。当创造原则指导具体实践时，不同维度、不同模型和不同情境的确定位置就应运而生。首先，从空间维度看，同种类型的位置确定，在不同维度中，前后知识存在内在联系，结构呈现螺旋上升趋势，如“线段中点的位置”在一维空间，而“数对确定位置”则在二维空间，这里的“数对”其实就是两个维度上“线段中点的位置”的有机整合;不同类型的位置确定，在相同维度中，考虑的关键要素的数量相同，如所有在二维空间的位置确定，都要锁定两个关键信息，才能精准定位物体的位置。其次，从模型建构看，直角坐标系和极坐标系是两种基本模型，模型内部要素的先后顺序根据实际需要约定，如用“距离+距离”的方式描述位置，约定“先列后行”;用“方向+距离”的方式描述位置，约定“先方向后距离”;用“角度+角度”的方式描述位置，约定“先经度后纬度”等，这样处理让确定位置的数学模型结构稳定，方便表达和交流。最后，从情境适用看，两种模型都在研究确定对象与参照物之间的位置关系，但是就小学生的理解水平而言，直角坐标系（只出现第一象限）侧重“点与整体”之间的位置关系，极坐标系侧重“点与点”之间的位置关系。到了第三学段，又统整为“用数对确定位置”，这里的“数对”已经实现对具体模型的超越，充分体现二维空间确定位置的数学本质。显然，数学中的确定位置融合“实际生活需要”和“简洁表达需要”，凸显数形结合、一一对应和符号表示等数学思想，既服務于数学的有序建构，也服务于学生的可持续发展。

3.教育中的确定位置

教育不但要“教知识”，而且要“育人品”;教育是有目的的执行，也有情怀的担当;教育不仅传承文明，更要发展创造。因此，教什么？怎么教？教到什么程度？等，是我们必须直面和厘清的问题。下面将从两个“点”进行梳理：一是通过具体的静态文本，能教给学生哪些必要的动态技能，教则清晰到位（在平面内确定位置需要考虑原点（观测点）、方向和单位，用有序数对的形式确定的是唯一的点;反过来，一个点也只需要有序数对就能唯一确定，点和有序数对之间一一对应），使学生能灵活运用，有针对性地解决一些相关问题，这是教育的保值点;二是经历知识的生长过程，能孕育哪些必要的思想品格，育则指向明确（在平面内确定位置需要锁定两个关键信息，还需要约定数学的表达方式，创造的外形可以因需而定，内在的本质却是相同的），并能内化迁移，使知识之间有效衔接，为后续学习提供智慧思考的路径和澎湃人生的精神，实现“教是为了更好地学”，这是教育的增值点。显然，教育中确定位置需要“保值”与“增值”的有机融合、互相促进和辩证统一。

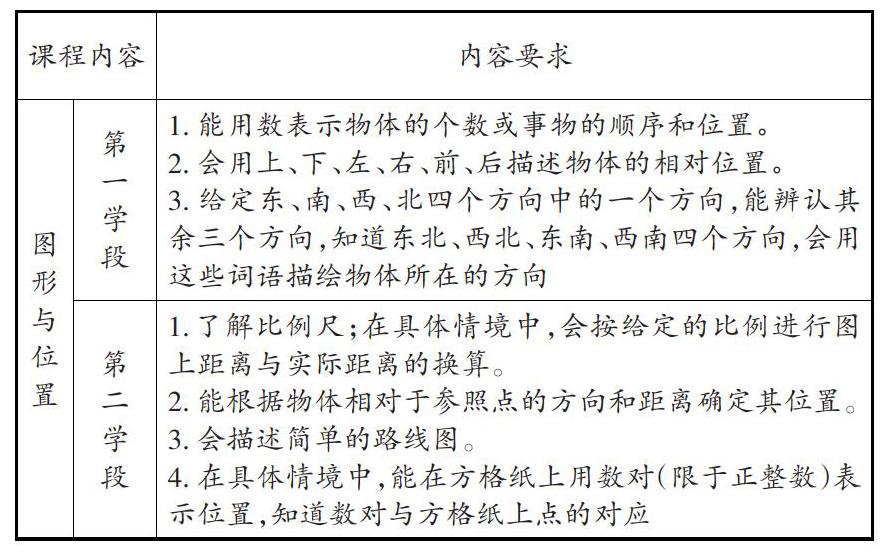
二、“确定位置”的内容要求

小学阶段的教学有其自身的特殊性，怎样的编排才能深入浅出地引导学生建构平面坐标雏形？怎样的架构能恰到好处，助推学生空间观念的发展？《义务教育数学课程标准（2011年版）》都做了具体回应和详细安排，参见下表。

苏教版教材就从三个层次落实课程标准要求，即平面内“点在线中的位置”、“点在面中的位置”和“点与点的位置”。其中，一年级上册“认位置”，以确定“练习本与数学书的相对位置”为例，运用“前后、左右、上下”简单描述“点与点的位置”;学完序数之后，结合“第几个”，以“确定队伍中某个人的位置”为例，来精准定位“点在线中的位置”。二年级下册“认识方向”，以确定“观测点的不同方向内的物体”为例，运用“东、南、西、北，东南、东北、西南、西北”，来模糊定位“点与点的位置”;四年级下册“确定位置”，以确定“教室内小军的位置”为例，运用“第几列”和“第几行”纵横交错产生的数对，精准定位“点在面中的位置”，是在二维空间中思考，渗透的是平面直角坐标系的数学模型;六年级下册“确定位置”，以确定“灯塔在轮船的具体位置”为例，运用“方向”和“距离”，精准定位“点与点的位置”，也是在二维空间中思考，但渗透的是平面极坐标系的数学模型。显然，教材的编排凸显了内容的生活化与数学化、记录的模糊性与精确性、思维的层次性与连续性的有机整合、辩证统一和有序发展。

对于“确定位置”专题的学习要求，课程标准明确指出，引导学生“经历图形的位置确定过程”，帮助学生“想象出物体的方位和相互之间的位置关系”，建立相应的位置模型，发展学生的空间观念。

三、“确定位置”的数学化教学路径

荷兰著名教育家、数学家弗赖登塔尔认为：“所谓数学化，就是人们运用数学的方法观察现实世界，分析研究各种具体现象，并加以整理组织的过程。”显然，位置确定的数学化教学路径，既有生活到数学的建模，也有数学到数学的推理，还有数学特有的不断抽象，但都指向数学本身，服务于学生发展，共同演绎现实主义的教学。

1.创设情境，引发学生的数学思考

情境是数学化教学的“调味剂”。适切的情境创设，不但能使课堂引入变得“亲近、轻松和亲切”，有效调用学生的主体经验，而且能使枯燥冰冷的数学知识饱含“温度、梯度和适度”，有针对性地引发学生的数学思考。

以“用数对确定位置”的教学为例。一是创设生活情境，典型的是运用主题图“小军坐在哪里？”，可看作是直接式引入;而“怎样找到电影票中的座位？”则通过调用观影经验，使学生感受到位置确定“有角度和有方法”，然后带着体验和收获再回到教室，可看作是間接式引人。二是创设游戏情境，设计“麦田打地鼠”“连连看”“排雷”等游戏，虽然玩法上有单一式和互动式的区分，但都是通过玩游戏的方式，引导学生体验和感受要想玩好游戏，必须考虑位置确定的具体性和简洁性。三是创设历史情境，从“笛卡儿与小蜘蛛的故事”人手，设计“如何确定小蜘蛛的位置？”的问题情境，将位置确定从一维“数射线”的描述逐步引向二维“数射线”的建构。显然，情境的主题类型和外在形式可以不同，但情境的角色定位和内在作用却要指向明确，也就是说，要立足学生实际且能引发学生的数学思考。

2.过程经历，演绎知识的“再创造”

“再创造”是数学化教学的“路线图”，是针对学生“囫囵吞枣”地获得“精密数学”的异化现象而提出的现实策略，提倡学生像“专家一样思考和体验”，完整经历知识的创造过程，把握问题的来龙去脉、外在表征和内在结构。

以“用方向和距离确定位置”的教学为例。首先，创设因天气恶劣影响船只航行的情境，使学生感受确定位置的紧迫性。接着，锁定学生汇报中出现频率最多的“东北方向”和“30千米”，发现距离30千米且在东北方向的点有许多，提出“不具体，怎么办？”的问题;当学生提出“1点钟方向”和“量角器测量”等隐含角度之后，可直接动态给出角度，记录成“北偏东30。和“东偏北60°”，引发学生“不统一，怎么办？”的思考，学生结合经验和生活情境，选择“南北”作为起点，此时可顺势指导学生将“四面八方”换个角度描述，如“东北”记录为“北偏东”等。最后，将反思改造后的关键信息“北偏东30°方向”和“30千米”同时呈现，让学生尝试组合信息，并提出“不规范，怎么办？”的问题，学生结合实际经验和已有概念，就能得出“方向优先”的数学意义和现实价值。显然，教学聚焦“人为规定”，放大创造过程，能助推学生感受知识的自然生长和精神的内在拔节。

3.纵横对比，建构模型的结构特征

对比是数学化教学的“好助手”。巧妙的对比，能够引发学生主动参与和深度思考，尤其是凸显特殊与特殊、特殊与一般的对比思考，更有助于学生空间观念的阶段式达成和有序性发展。

首先看横向对比，如为什么在队伍中，相同的位置可以用“从左往右第3个”和“从右往左第4个”不同的方式描述？对比体会观测的方向;为什么数对（1，5）和（5，1）的数字相同，表示的位置却不同？对比内化数对的结构;“灯塔1在轮船的北偏东30～方向30千米处”，而“轮船在灯塔1的南偏西30°方向30千米处”，同样的两个点，位置描述为什么不一样？对比体验位置的相对。接着看纵向对比，如为什么学习了数对确定位置，还要学习用方向和距离确定位置，两者之间有什么相同点和不同点？比相同点，要锁定两个关键信息才能完整表达，而且要约定数学表达方式才能统一表征;再比不同点，关键信息的内容有差异，前者锁定的是列和行，后者关注的是方向和距离，模型适用的情境不一样，前者侧重“点与整体”的位置描述，后者适合“点与点”的位置记录。显然，纵横对比凸显了模型外在特征的差异性和内在结构的一致性。

4.渗透思想，内化关键的能力品质

思想是数学化教学的“生命线”。相对于明线的方法技能，暗线的数学思想更具魅力，更容易迁移，对学生终身发展来说，也更具特定的意义和作用。

首先，从生活到数学需要抽象，如“用数对确定位置”经历“实物图一点子图一坐标图”的抽象;从数学到数学也需要抽象，如将“4列3行”“4↑3→”“4、3”等抽象为（4，3），是对抽象的“再抽象”。接着，从点到面需要归纳推理，如逐步出示“南偏东”“80°”“50千米”等条件，在“猜神秘岛位置”的游戏中，归纳推理出“面一线一点”的路径;从面到点需要演绎推理，如确定位置路径的具体运用;从面（点）到面（点）需要类比推理，如“用数对确定位置”有观测点、方向和距离，类比推理出影响“用方向和距离确定位置”的可能因素。最后，从生活世界到数学研究需要模型建构，如“用数对确定位置”抽象建构成“距离+距离”，“用方向和距离确定位置”抽象建构成“方向+距离”等;从数学世界回归生活需要“变模运用”，如“棋盘中的棋子位置”“公交车上的乘客位置”“地图上两地的位置”等。显然，通过抽象，外部世界进入了数学;通过推理，促进了数学自身的发展，而模型思想建构了数学与现实世界的联系桥梁。

数学化教学路径注重横向数学化与纵向数学化结伴而行、因需侧重，凸显情境的服务、过程的完整、方法的对比和思想的渗透。这样，外在生动与内在深刻相映生辉，实现为未知而教;知识技能与核心素养融合共生，实现为未来而学。

（责编金铃）