小学数学微实验指导框架
陈静燕
[摘要]对于小学低年段数学教学,以自主探索、合作探究为特点的课外数学实验是一种重要的数学学习补充方式。以实验案例分析的方式,从方案设计、调节反省、操作探究及评价反思四个方面入手,给出指导小学低年段数学实验的框架,积极引入数学微实验的教学方法。
[关键词]数学微实验;自主学习;范式
[中图分类号]G623.5 [文献标识码]A [文章编号]1007-9068(2020)14-0017-02
一、方案设计:发展学生智慧。转变学习方式
美国教育学家布鲁纳认为:教师不应只注重知识的传授,还应该强调智慧的发展。认识是一个过程而非结果,教学的目的不是记忆知识,而是帮助学生依据现实生活中所获得的感性材料,借助推理和直觉提出试探性的假设,鼓励学生用更多的感性材料对此做检验。数学微实验能够再现数学的发现过程,是一条解决数学问题的全新思路。
1.实验猜想:寻找认知冲突,引发实验需求
数学实验鼓励学生在生活中发现矛盾、设置矛盾,从而引发学生的认知冲突。例如,二年级的小盛提出的“我比爸妈走得快?”的问题就可以作为探索规律的数学实验。
[实验猜想]
在地铁站、火车站、机场等地方经常能看到自动人行道。人们可以把行李放在上面,轻松地经过一段长长的距离。但是我更喜欢在上面快速地走着,一眨眼就能到达另一头,然后等着爸爸妈妈从后面慢悠悠地跟过来。那么,为什么我会比爸爸妈妈更快地到达终点呢?
2.实验解读:数学化组织,重视伙伴力量
数学实验最终能否发挥选题的价值和应有效益,需要教师对数学实验的教学过程进行“数学化”的组织。可以结合转化、抽象及数形结合的思想,在实验过程中突出实验的数学属性和数学学习特性,在进行实验解读阶段,要注意为后续实验的设计以及实验结果的归纳做好铺垫。
[实验准备]
生1:站在自动人行道上速度最快,因为它是自动的。
生2:不对,我在平地上走路最快。
生3:在自动人行道上,一边传送、一边走最快!
在思考数学课题时,学生经常会产生不同的意见,这就表明数学实验的活动方式能激发学生主动参与数学学习的热情。
二、调节反省:注重学科整合,探索条件与结论的关联性
放眼数学的发展历程,从结绳计数开始,到建立金字塔,甚至更高阶的微积分等,本质上都是一个个实验过程。要将数学自身的魅力转化成学习者能够体验到的成功经验,就需要对学习过程进行有效调节。例如,帮助实验者设计合适的操作步骤,给实验者提供可行的活动方案,使其将实验想法付诸实践。
[实验方法]
(1)用平时走路的速度走完静止的自动人行道所需的时间(t1)。
(2)站在前进的自动人行道上“走”完自动人行道所需的时间(t2)。
(3)用平时走路的速度在前进的自动人行道上行走所需的时间(t3)。
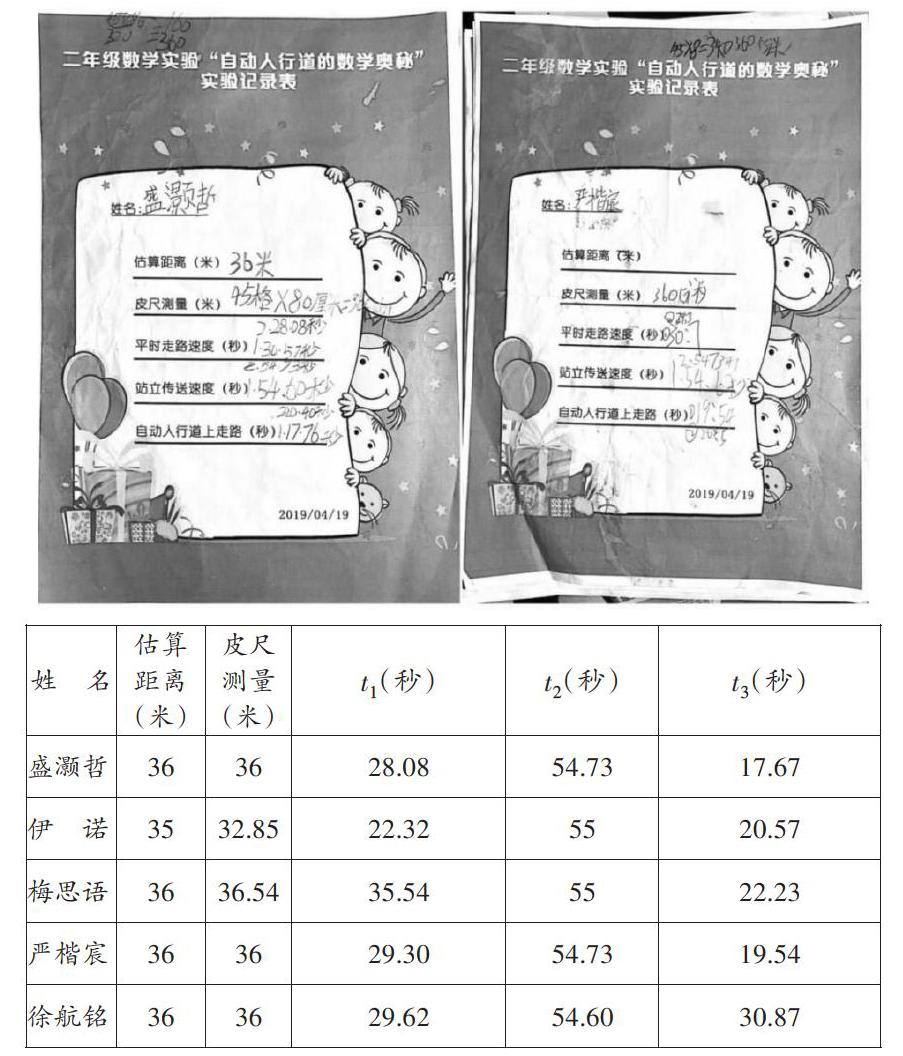
[实验记录]
团队汇总表:
1.转变课程观念,大胆创造机会
现行的课程设置方式将学科教学按课时划分,按照课表固定授课,导致教师只能固守传统的教学模式,常常因为害怕影响教学进度而放弃数学实验。教师应该充分认识数学实验的价值,拥有打破固有观念和教学安排的勇气,为数学实验的开展创造机会和条件。
2.进行学科整合,完善认知结构
数学知识从来都不是孤立的,数学学习就是在知识间的纵横联系中不断丰富数学素养。教师要注重不同学科间的联系,让学生在学习各学科知识的同时,通过数学实验体会数学知识的基础性、广泛性和应用性。
3.打破课内、课外学习的壁垒,链接生活
数学实验不应该局限于教室,既可以在校园进行,也可以在校外进行,还可以采取课内外相结合的方式,节约课堂时间。对于本文的案例,笔者课后指导学生进行计算整理和统计,在课上进行展示、交流,全班围绕实验结果进行分析、讨论。
三、操作探究:明确实验步骤,规范操作统计
[实验步骤]
第一步:估算自动人行道的长度。有的学生用“迈步测量法”;有的学生用“计算地面地砖”的方法。
第二步:用皮尺测量自动人行道的长度。小组组员分别记录在自己的表格上,测量结果的单位为米、分米、厘米、毫米。
第三步:记录三种走法的时间。
第四步:分析结果,比较数据。
[实验结果]
估算:(1)每步长约50厘米,通过计算步数,估算得出36.54米。
(2)计算地面上的大理石砖:45格×80厘米=3600(厘米)。
实测:自动人行道的实际长度是36米。
1.注重提前估算,联系新旧知识
《美国学校数学课程与评价标准》指出,培养估算意识,不应该在课堂上,而应该在具体的问题情境中。首先确定是否需要计算,然后再根据答案的性质来选择合适的计算方法。在之前的长度的測量练习中,很少需要学生估算,大部分直接采用用尺测量的方法。面对生活中一段需要估算的实际距离时,学生就会产生认知冲突。估算培养的是直观能力,是在问题情境中对数量运算的一种直观优化。
2.先推理再验证,整合思考方式
学生的数学学习过程充满着猜测、验证、推理、想象,当学生对基本事实有了一定的感知后,要引导学生沟通猜想与结论之间的联系,就需要推理和想象的补充。笔者指导学生推理:走路的快慢涉及的变量就是走路的时间,与此变量相关的因素是什么?学生经过讨论推理,得出结论:与人行道的长度无关,和通过的速度有关,只需要验证三种情况下通过的速度不同,通过的时间就会不同。
四、评价反思:优化评价方法,培养衍生思维
数学实验过程中的回顾反思不仅是对实验步骤的简单回顾,还要指导学生从实验步骤中总结与提炼数学的基本思想方法。评价在教学中起着极其重要的作用。以往的评价更多指向知识的形成与掌握,缺少对数学思维发展类的评价,忽略对生活应用能力和创新能力的评价。
[实验结论]
(1)站立不动,传送到终点所用的时间都是一样的,55秒;在前行的自动人行道上行走,到达终点的时间是最短的,平均只要25秒左右。
(2)自动人行道,实际上是为了让那些赶时间的人快速通过。
(3)有误差是数学实验中存在的正常现象。
[衍生思维]
生活中还有类似的场景:运货的大船在京杭大运河上航行,假设水流的方向和船开行的方向一样,船是不是就会开得更快?
皮亚杰的认知发展理论提醒我们:教育教学要给学生提供大量的、丰富的、真实环境中创造的活动,让学生自主发现知识;要在教学中创设一些使学生产生认知不平衡的问题,促进学生认知的发展;关注学生的思维过程,让学生多参与社会活动。数学实验的设计正是与皮亚杰的认知发展理论高度契合,让数学实验走进数学课堂,让学生走进数学实验,在数学实验中,在动手操作中不断提升数学素养,最终达到“为学而教”的教学目标。

